
Question Number 67018 by mathmax by abdo last updated on 21/Aug/19
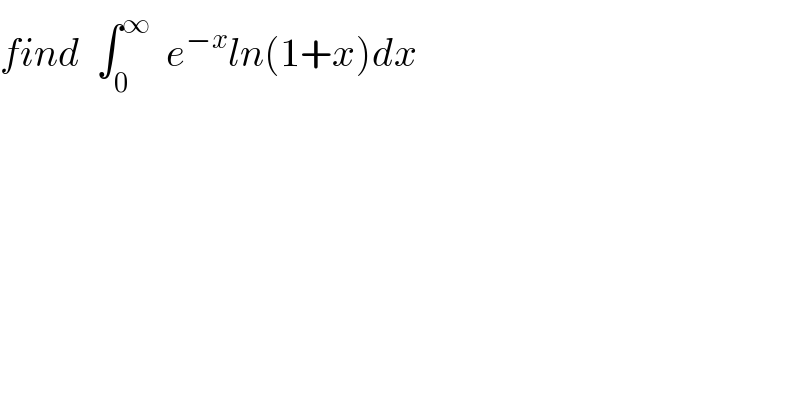
$${find}\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{x}} {ln}\left(\mathrm{1}+{x}\right){dx} \\ $$
Commented by mathmax by abdo last updated on 24/Aug/19
![let I =∫_0 ^∞ e^(−x) ln(1+x)dx ⇒I =_(1+x=t) ∫_1 ^(+∞) e^(−(t−1)) ln(t)dt =e ∫_1 ^(+∞) e^(−t) ln(t)dt we have ∫_0 ^∞ e^(−t) ln(t)dt =−γ ⇒ ∫_0 ^1 e^(−t) ln(t)dt +∫_1 ^(+∞) e^(−t) ln(t)dt =−γ ⇒ ∫_1 ^(+∞) e^(−t) ln(t)dt =−γ−∫_0 ^1 e^(−t) ln(t)dt we have ∫_0 ^1 e^(−t) ln(t)dt =∫_0 ^1 (Σ_(n=0) ^∞ (((−1)^n t^n )/(n!))ln(t))dt =Σ_(n=0) ^∞ (((−1)^n )/(n!)) ∫_0 ^1 t^n ln(t)dt let A_n =∫_0 ^1 t^n ln(t)dt by parts A_n =[(t^(n+1) /(n+1))ln(t)]_0 ^1 −∫_0 ^1 (t^(n+1) /(n+1))(dt/t) =−(1/(n+1)) ∫_0 ^1 t^n dt =−(1/((n+1)^2 )) ⇒ ∫_0 ^1 e^(−t) ln(t)dt =−Σ_(n=0) ^∞ (((−1)^n )/(n!(n+1)^2 )) ⇒ I =−eγ+e Σ_(n=0) ^∞ (((−1)^n )/(n!(n+1)^2 )) ⇒ I =−eγ +e{1−(1/2^2 ) +(1/(2! 3^2 ))−(1/(3!4^2 ))+....} and 10 terms give a best approximation of I (γ is number of euler)](Q67218.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}} {ln}\left(\mathrm{1}+{x}\right){dx}\:\Rightarrow{I}\:=_{\mathrm{1}+{x}={t}} \:\:\:\int_{\mathrm{1}} ^{+\infty} {e}^{−\left({t}−\mathrm{1}\right)} {ln}\left({t}\right){dt} \\ $$$$={e}\:\int_{\mathrm{1}} ^{+\infty} \:{e}^{−{t}} {ln}\left({t}\right){dt}\:\:{we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} {ln}\left({t}\right){dt}\:=−\gamma\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{t}} {ln}\left({t}\right){dt}\:+\int_{\mathrm{1}} ^{+\infty} {e}^{−{t}} {ln}\left({t}\right){dt}\:=−\gamma\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:{e}^{−{t}} {ln}\left({t}\right){dt}\:=−\gamma−\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{t}} {ln}\left({t}\right){dt}\:\:{we}\:{have} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{t}} {ln}\left({t}\right){dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {t}^{{n}} }{{n}!}{ln}\left({t}\right)\right){dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}} {ln}\left({t}\right){dt}\:\:{let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}} {ln}\left({t}\right){dt}\:\:{by}\:{parts} \\ $$$${A}_{{n}} =\left[\frac{{t}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{ln}\left({t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\frac{{dt}}{{t}}\:=−\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}} {dt}\:=−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{t}} {ln}\left({t}\right){dt}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=−{e}\gamma+{e}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=−{e}\gamma\:+{e}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}!\:\mathrm{3}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}!\mathrm{4}^{\mathrm{2}} }+....\right\} \\ $$$${and}\:\mathrm{10}\:{terms}\:{give}\:{a}\:{best}\:{approximation}\:{of}\:{I} \\ $$$$\left(\gamma\:{is}\:{number}\:{of}\:{euler}\right) \\ $$$$ \\ $$
