Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 6914 by Tawakalitu. last updated on 02/Aug/16

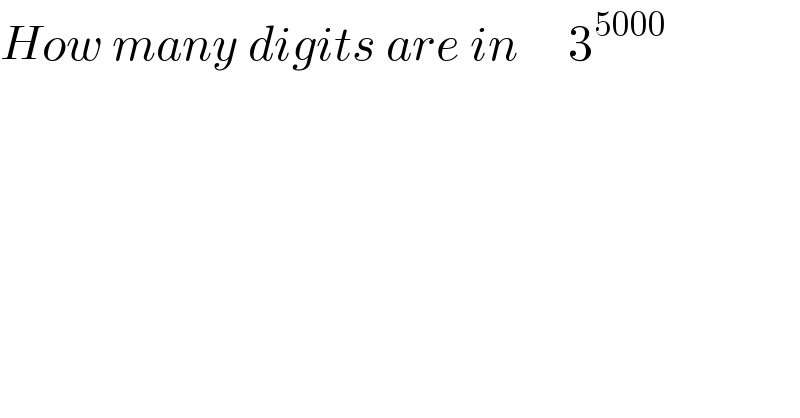
How many digits are in 3^(5000)

$${How}\:{many}\:{digits}\:{are}\:{in}\:\:\:\:\:\mathrm{3}^{\mathrm{5000}} \\ $$

Commented by Rasheed Soomro last updated on 03/Aug/16

3^1 =3 (1 digit) , 3^2 =9 (1 digit) 3^3 =27(2 digits), 3^4 =81(2 digits) 3^5 =243 (3digits),3^6 =729 3^7 =2187,3^8 =6561 (4 digits) ⋮ Let d is number of digits in lhs We can easily conclude that 3^(2d−1) (odd power) and 3^(2d) (even power) both have d digits Now 3^(5000) =3^(2d) 2d=5000⇒d=((5000)/2)=2500 3^(5000) =3^(2(2500)) Hence number of digits=∣2500∣_(−) ^(−) in 3^(5000)

$$\mathrm{3}^{\mathrm{1}} =\mathrm{3}\:\left(\mathrm{1}\:{digit}\right)\:,\:\mathrm{3}^{\mathrm{2}} =\mathrm{9}\:\left(\mathrm{1}\:{digit}\right) \\ $$$$\mathrm{3}^{\mathrm{3}} =\mathrm{27}\left(\mathrm{2}\:{digits}\right),\:\mathrm{3}^{\mathrm{4}} =\mathrm{81}\left(\mathrm{2}\:{digits}\right) \\ $$$$\mathrm{3}^{\mathrm{5}} =\mathrm{243}\:\left(\mathrm{3}{digits}\right),\mathrm{3}^{\mathrm{6}} =\mathrm{729} \\ $$$$\mathrm{3}^{\mathrm{7}} =\mathrm{2187},\mathrm{3}^{\mathrm{8}} =\mathrm{6561}\:\left(\mathrm{4}\:{digits}\right) \\ $$$$\vdots \\ $$$${Let}\:{d}\:{is}\:{number}\:{of}\:\:{digits}\:{in}\:{lhs} \\ $$$${We}\:{can}\:{easily}\:{conclude}\:{that} \\ $$$$\mathrm{3}^{\mathrm{2}{d}−\mathrm{1}} \left({odd}\:{power}\right)\:{and}\:\mathrm{3}^{\mathrm{2}{d}} \left({even}\:{power}\right)\:{both}\:{have}\:{d}\:{digits} \\ $$$${Now}\:\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{5000}} =\mathrm{3}^{\mathrm{2}{d}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{d}=\mathrm{5000}\Rightarrow{d}=\frac{\mathrm{5000}}{\mathrm{2}}=\mathrm{2500} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{5000}} =\mathrm{3}^{\mathrm{2}\left(\mathrm{2500}\right)} \\ $$$$\:\:\:\:\:\:\:{Hence}\:{number}\:{of}\:{digits}=\underset{−} {\overline {\mid\mathrm{2500}\mid}}\:{in}\:\mathrm{3}^{\mathrm{5000}} \\ $$

Commented by Tawakalitu. last updated on 02/Aug/16

Thanks so much

$${Thanks}\:{so}\:{much} \\ $$

Commented by sandy_suhendra last updated on 02/Aug/16

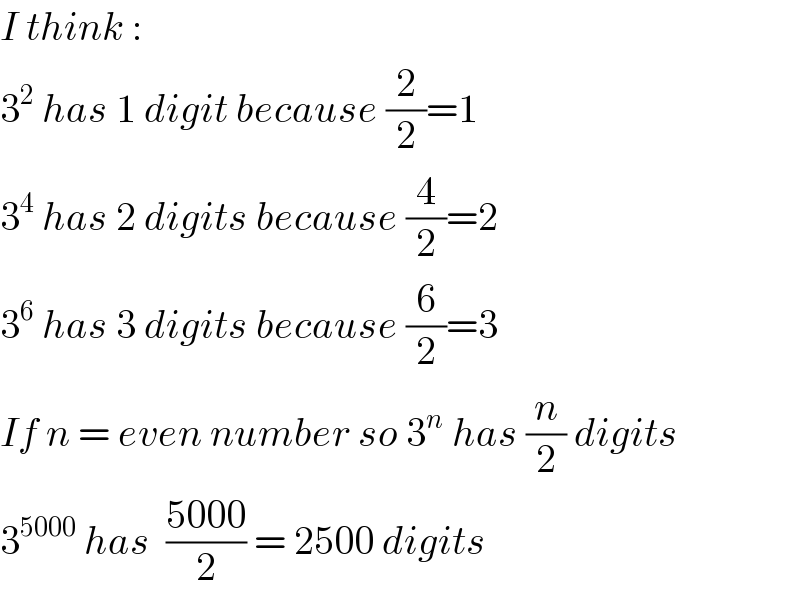
I think : 3^2 has 1 digit because (2/2)=1 3^4 has 2 digits because (4/2)=2 3^6 has 3 digits because (6/2)=3 If n = even number so 3^n has (n/2) digits 3^(5000) has ((5000)/2) = 2500 digits

$${I}\:{think}\:: \\ $$$$\mathrm{3}^{\mathrm{2}} \:{has}\:\mathrm{1}\:{digit}\:{because}\:\frac{\mathrm{2}}{\mathrm{2}}=\mathrm{1} \\ $$$$\mathrm{3}^{\mathrm{4}} \:{has}\:\mathrm{2}\:{digits}\:{because}\:\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2} \\ $$$$\mathrm{3}^{\mathrm{6}} \:{has}\:\mathrm{3}\:{digits}\:{because}\:\frac{\mathrm{6}}{\mathrm{2}}=\mathrm{3} \\ $$$${If}\:{n}\:=\:{even}\:{number}\:{so}\:\mathrm{3}^{{n}} \:{has}\:\frac{{n}}{\mathrm{2}}\:{digits} \\ $$$$\mathrm{3}^{\mathrm{5000}} \:{has}\:\:\frac{\mathrm{5000}}{\mathrm{2}}\:=\:\mathrm{2500}\:{digits} \\ $$

Commented by Rasheed Soomro last updated on 03/Aug/16

Thanks Sandy.I had made a mistake in my answer. Now I have corrected it.

$${Thanks}\:{Sandy}.{I}\:{had}\:{made}\:{a}\:{mistake}\:{in}\:{my}\:{answer}. \\ $$$${Now}\:{I}\:{have}\:{corrected}\:{it}. \\ $$$$ \\ $$

Answered by nume1114 last updated on 03/Aug/16

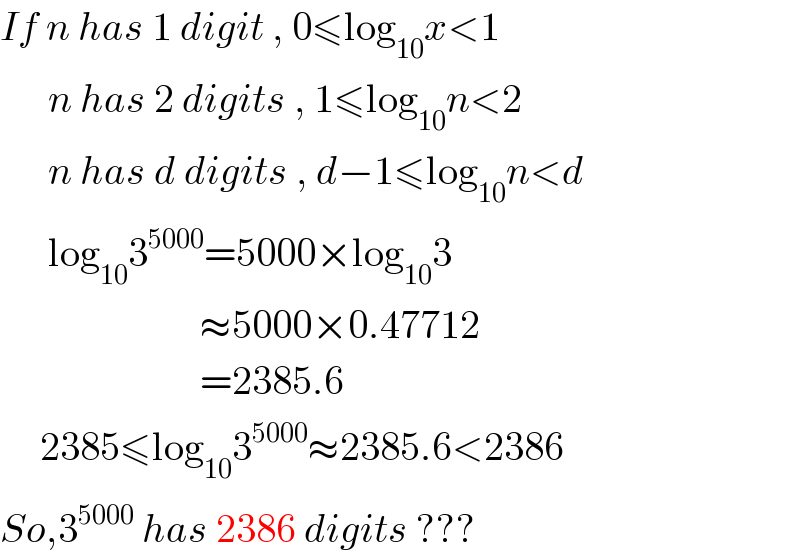
If n has 1 digit , 0≤log_(10) x<1 n has 2 digits , 1≤log_(10) n<2 n has d digits , d−1≤log_(10) n<d log_(10) 3^(5000) =5000×log_(10) 3 ≈5000×0.47712 =2385.6 2385≤log_(10) 3^(5000) ≈2385.6<2386 So,3^(5000) has 2386 digits ???

$${If}\:{n}\:{has}\:\mathrm{1}\:{digit}\:,\:\mathrm{0}\leqslant\mathrm{log}_{\mathrm{10}} {x}<\mathrm{1} \\ $$$$\:\:\:\:\:\:{n}\:{has}\:\mathrm{2}\:{digits}\:,\:\mathrm{1}\leqslant\mathrm{log}_{\mathrm{10}} {n}<\mathrm{2} \\ $$$$\:\:\:\:\:\:{n}\:{has}\:{d}\:{digits}\:,\:{d}−\mathrm{1}\leqslant\mathrm{log}_{\mathrm{10}} {n}<{d} \\ $$$$\:\:\:\:\:\:\mathrm{log}_{\mathrm{10}} \mathrm{3}^{\mathrm{5000}} =\mathrm{5000}×\mathrm{log}_{\mathrm{10}} \mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\approx\mathrm{5000}×\mathrm{0}.\mathrm{47712} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2385}.\mathrm{6} \\ $$$$\:\:\:\:\:\mathrm{2385}\leqslant\mathrm{log}_{\mathrm{10}} \mathrm{3}^{\mathrm{5000}} \approx\mathrm{2385}.\mathrm{6}<\mathrm{2386} \\ $$$${So},\mathrm{3}^{\mathrm{5000}} \:{has}\:\mathrm{2386}\:{digits}\:??? \\ $$

Commented by Yozzii last updated on 03/Aug/16

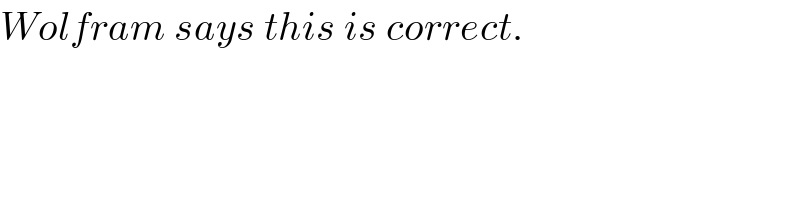
Wolfram says this is correct.

$${Wolfram}\:{says}\:{this}\:{is}\:{correct}. \\ $$

Commented by Rasheed Soomro last updated on 03/Aug/16

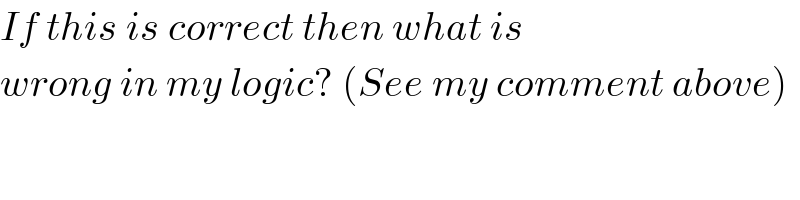
If this is correct then what is wrong in my logic? (See my comment above)

$${If}\:{this}\:{is}\:{correct}\:{then}\:{what}\:{is} \\ $$$${wrong}\:{in}\:{my}\:{logic}?\:\left({See}\:{my}\:{comment}\:{above}\right) \\ $$

Commented by FilupSmith last updated on 03/Aug/16

is there a way to prove your logic?

$$\mathrm{is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{way}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{your}\:\mathrm{logic}? \\ $$

Commented by Yozzii last updated on 03/Aug/16

Wolfram indicates that the pattern you have found works for small d∈N. It doesn′t work for d=15 for example. 3^(29) has 14 digits while 3^(30) has 15 digits. 3^(5000) =1×10^(5000log_(10) 3) 0.476<log_(10) 3<0.48 ⇒10^(2380) =10^(0.476×5000) <10^(5000log_(10) 3) <10^(5000×0.48) =1×10^(2400) ⇒3^(5000) has decimal length between 2381 and 2401 This is based on approximations of log_(10) 3. So, a good approximation is log_(10) 3≈0.477121254 ⇒0.47712<log_(10) 3<0.47720 ⇒10^(5000×0.47712) <3^(5000) <10^(5000×0.4772) 10^(2385.6) <3^(5000) <10^(2386) 10^(0.6) ×10^(2385) <3^(5000) <10^(2386) ⇒3^(5000) must have 2386 digits since it cannot exceed 1×10^(2386) which has 2387 digits (1×10^(2386) is smallest integer>0 with 2387 digits) but is greater than 10^(0.6) ×10^(2385) which has 2386 digits if we approximate 10^(0.6) to an integer (10^(0.6) ≈4).

$${Wolfram}\:{indicates}\:{that}\:{the}\:{pattern} \\ $$$${you}\:{have}\:{found}\:{works}\:{for}\:{small}\:{d}\in\mathbb{N}. \\ $$$${It}\:{doesn}'{t}\:{work}\:{for}\:{d}=\mathrm{15}\:{for}\:{example}. \\ $$$$\mathrm{3}^{\mathrm{29}} \:{has}\:\mathrm{14}\:{digits}\:{while}\:\mathrm{3}^{\mathrm{30}} \:{has}\:\mathrm{15}\:{digits}. \\ $$$$\mathrm{3}^{\mathrm{5000}} =\mathrm{1}×\mathrm{10}^{\mathrm{5000}{log}_{\mathrm{10}} \mathrm{3}} \\ $$$$\mathrm{0}.\mathrm{476}<{log}_{\mathrm{10}} \mathrm{3}<\mathrm{0}.\mathrm{48} \\ $$$$\Rightarrow\mathrm{10}^{\mathrm{2380}} =\mathrm{10}^{\mathrm{0}.\mathrm{476}×\mathrm{5000}} <\mathrm{10}^{\mathrm{5000}{log}_{\mathrm{10}} \mathrm{3}} <\mathrm{10}^{\mathrm{5000}×\mathrm{0}.\mathrm{48}} =\mathrm{1}×\mathrm{10}^{\mathrm{2400}} \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{5000}} \:{has}\:{decimal}\:{length}\:{between}\:\mathrm{2381}\:{and}\:\mathrm{2401} \\ $$$${This}\:{is}\:{based}\:{on}\:{approximations}\:{of}\:{log}_{\mathrm{10}} \mathrm{3}. \\ $$$${So},\:{a}\:{good}\:{approximation}\:{is}\: \\ $$$${log}_{\mathrm{10}} \mathrm{3}\approx\mathrm{0}.\mathrm{477121254} \\ $$$$\Rightarrow\mathrm{0}.\mathrm{47712}<{log}_{\mathrm{10}} \mathrm{3}<\mathrm{0}.\mathrm{47720} \\ $$$$\Rightarrow\mathrm{10}^{\mathrm{5000}×\mathrm{0}.\mathrm{47712}} <\mathrm{3}^{\mathrm{5000}} <\mathrm{10}^{\mathrm{5000}×\mathrm{0}.\mathrm{4772}} \\ $$$$\mathrm{10}^{\mathrm{2385}.\mathrm{6}} <\mathrm{3}^{\mathrm{5000}} <\mathrm{10}^{\mathrm{2386}} \\ $$$$\mathrm{10}^{\mathrm{0}.\mathrm{6}} ×\mathrm{10}^{\mathrm{2385}} <\mathrm{3}^{\mathrm{5000}} <\mathrm{10}^{\mathrm{2386}} \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{5000}} \:{must}\:{have}\:\mathrm{2386}\:{digits}\:{since}\:{it}\:{cannot} \\ $$$${exceed}\:\mathrm{1}×\mathrm{10}^{\mathrm{2386}} \:{which}\:{has}\:\mathrm{2387}\:{digits}\:\left(\mathrm{1}×\mathrm{10}^{\mathrm{2386}} \:{is}\:{smallest}\:{integer}>\mathrm{0}\:{with}\:\mathrm{2387}\:{digits}\right) \\ $$$${but}\:{is}\:{greater}\:{than}\:\mathrm{10}^{\mathrm{0}.\mathrm{6}} ×\mathrm{10}^{\mathrm{2385}} \:{which}\:{has} \\ $$$$\mathrm{2386}\:{digits}\:{if}\:{we}\:{approximate}\:\mathrm{10}^{\mathrm{0}.\mathrm{6}} \:{to}\:{an} \\ $$$${integer}\:\left(\mathrm{10}^{\mathrm{0}.\mathrm{6}} \approx\mathrm{4}\right). \\ $$

Commented by nume1114 last updated on 03/Aug/16

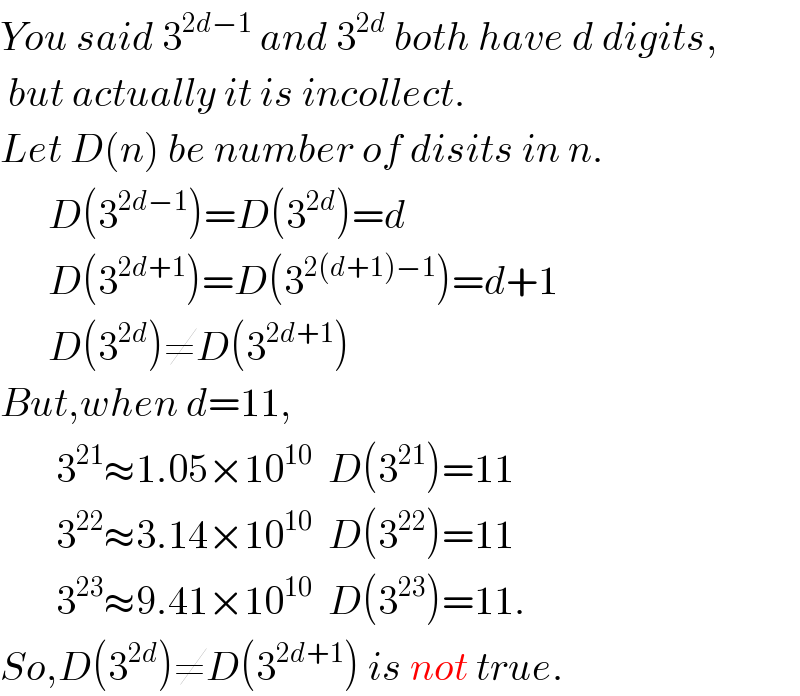
You said 3^(2d−1) and 3^(2d) both have d digits, but actually it is incollect. Let D(n) be number of disits in n. D(3^(2d−1) )=D(3^(2d) )=d D(3^(2d+1) )=D(3^(2(d+1)−1) )=d+1 D(3^(2d) )≠D(3^(2d+1) ) But,when d=11, 3^(21) ≈1.05×10^(10) D(3^(21) )=11 3^(22) ≈3.14×10^(10) D(3^(22) )=11 3^(23) ≈9.41×10^(10) D(3^(23) )=11. So,D(3^(2d) )≠D(3^(2d+1) ) is not true.

$${You}\:{said}\:\mathrm{3}^{\mathrm{2}{d}−\mathrm{1}} \:{and}\:\mathrm{3}^{\mathrm{2}{d}} \:{both}\:{have}\:{d}\:{digits}, \\ $$$$\:{but}\:{actually}\:{it}\:{is}\:{incollect}. \\ $$$${Let}\:{D}\left({n}\right)\:{be}\:{number}\:{of}\:{disits}\:{in}\:{n}. \\ $$$$\:\:\:\:\:\:{D}\left(\mathrm{3}^{\mathrm{2}{d}−\mathrm{1}} \right)={D}\left(\mathrm{3}^{\mathrm{2}{d}} \right)={d} \\ $$$$\:\:\:\:\:\:{D}\left(\mathrm{3}^{\mathrm{2}{d}+\mathrm{1}} \right)={D}\left(\mathrm{3}^{\mathrm{2}\left({d}+\mathrm{1}\right)−\mathrm{1}} \right)={d}+\mathrm{1} \\ $$$$\:\:\:\:\:\:{D}\left(\mathrm{3}^{\mathrm{2}{d}} \right)\neq{D}\left(\mathrm{3}^{\mathrm{2}{d}+\mathrm{1}} \right) \\ $$$${But},{when}\:{d}=\mathrm{11}, \\ $$$$\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{21}} \approx\mathrm{1}.\mathrm{05}×\mathrm{10}^{\mathrm{10}} \:\:{D}\left(\mathrm{3}^{\mathrm{21}} \right)=\mathrm{11} \\ $$$$\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{22}} \approx\mathrm{3}.\mathrm{14}×\mathrm{10}^{\mathrm{10}} \:\:{D}\left(\mathrm{3}^{\mathrm{22}} \right)=\mathrm{11} \\ $$$$\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{23}} \approx\mathrm{9}.\mathrm{41}×\mathrm{10}^{\mathrm{10}} \:\:{D}\left(\mathrm{3}^{\mathrm{23}} \right)=\mathrm{11}. \\ $$$${So},{D}\left(\mathrm{3}^{\mathrm{2}{d}} \right)\neq{D}\left(\mathrm{3}^{\mathrm{2}{d}+\mathrm{1}} \right)\:{is}\:{not}\:{true}. \\ $$

Commented by Rasheed Soomro last updated on 04/Aug/16

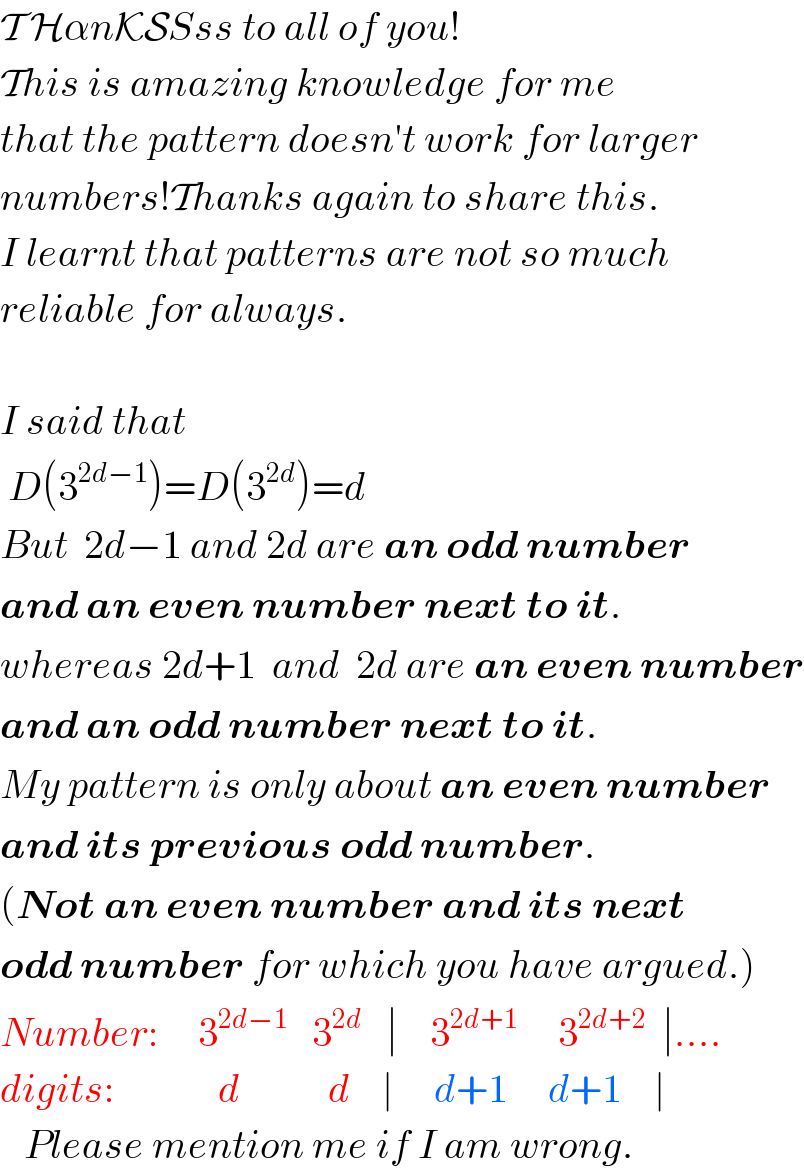
T HαnKSSss to all of you! This is amazing knowledge for me that the pattern doesn′t work for larger numbers!Thanks again to share this. I learnt that patterns are not so much reliable for always. I said that D(3^(2d−1) )=D(3^(2d) )=d But 2d−1 and 2d are an odd number and an even number next to it. whereas 2d+1 and 2d are an even number and an odd number next to it. My pattern is only about an even number and its previous odd number. (Not an even number and its next odd number for which you have argued.) Number: 3^(2d−1) 3^(2d) ∣ 3^(2d+1) 3^(2d+2) ∣.... digits: d d ∣ d+1 d+1 ∣ Please mention me if I am wrong.

$$\mathcal{T}\:\mathcal{H}\alpha{n}\mathcal{KS}{Sss}\:{to}\:{all}\:{of}\:{you}! \\ $$$$\mathcal{T}{his}\:{is}\:{amazing}\:{knowledge}\:{for}\:{me}\: \\ $$$${that}\:{the}\:{pattern}\:{doesn}'{t}\:{work}\:{for}\:{larger} \\ $$$${numbers}!\mathcal{T}{hanks}\:{again}\:{to}\:{share}\:{this}. \\ $$$${I}\:{learnt}\:{that}\:{patterns}\:{are}\:{not}\:{so}\:{much} \\ $$$${reliable}\:{for}\:{always}. \\ $$$$ \\ $$$${I}\:{said}\:{that} \\ $$$$\:{D}\left(\mathrm{3}^{\mathrm{2}{d}−\mathrm{1}} \right)={D}\left(\mathrm{3}^{\mathrm{2}{d}} \right)={d} \\ $$$${But}\:\:\mathrm{2}{d}−\mathrm{1}\:{and}\:\mathrm{2}{d}\:{are}\:\boldsymbol{{an}}\:\boldsymbol{{odd}}\:\boldsymbol{{number}} \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{an}}\:\boldsymbol{{even}}\:\boldsymbol{{number}}\:\boldsymbol{{next}}\:\boldsymbol{{to}}\:\boldsymbol{{it}}. \\ $$$${whereas}\:\mathrm{2}{d}+\mathrm{1}\:\:{and}\:\:\mathrm{2}{d}\:{are}\:\boldsymbol{{an}}\:\boldsymbol{{even}}\:\boldsymbol{{number}} \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{an}}\:\boldsymbol{{odd}}\:\boldsymbol{{number}}\:\boldsymbol{{next}}\:\boldsymbol{{to}}\:\boldsymbol{{it}}.\: \\ $$$${My}\:{pattern}\:{is}\:{only}\:{about}\:\boldsymbol{{an}}\:\boldsymbol{{even}}\:\boldsymbol{{number}} \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{its}}\:\boldsymbol{{previous}}\:\boldsymbol{{odd}}\:\boldsymbol{{number}}. \\ $$$$\left(\boldsymbol{{Not}}\:\boldsymbol{{an}}\:\boldsymbol{{even}}\:\boldsymbol{{number}}\:\boldsymbol{{and}}\:\boldsymbol{{its}}\:\boldsymbol{{next}}\right. \\ $$$$\left.\boldsymbol{{odd}}\:\boldsymbol{{number}}\:{for}\:{which}\:{you}\:{have}\:{argued}.\right) \\ $$$${Number}:\:\:\:\:\:\mathrm{3}^{\mathrm{2}{d}−\mathrm{1}} \:\:\:\mathrm{3}^{\mathrm{2}{d}} \:\:\:\mid\:\:\:\:\mathrm{3}^{\mathrm{2}{d}+\mathrm{1}} \:\:\:\:\:\mathrm{3}^{\mathrm{2}{d}+\mathrm{2}} \:\:\mid.... \\ $$$${digits}:\:\:\:\:\:\:\:\:\:\:\:\:\:{d}\:\:\:\:\:\:\:\:\:\:\:{d}\:\:\:\:\mid\:\:\:\:\:{d}+\mathrm{1}\:\:\:\:\:{d}+\mathrm{1}\:\:\:\:\mid \\ $$$$\:\:\:{Please}\:{mention}\:{me}\:{if}\:{I}\:{am}\:{wrong}. \\ $$

Commented by Tawakalitu. last updated on 03/Aug/16

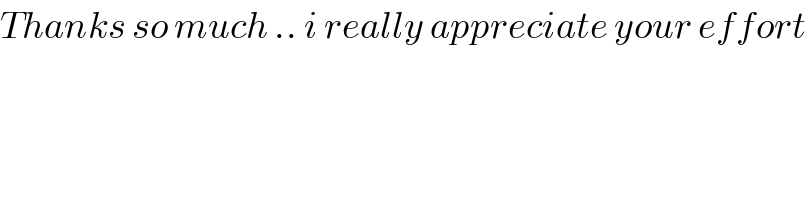
Thanks so much .. i really appreciate your effort

$${Thanks}\:{so}\:{much}\:..\:{i}\:{really}\:{appreciate}\:{your}\:{effort} \\ $$

Commented by nume1114 last updated on 04/Aug/16

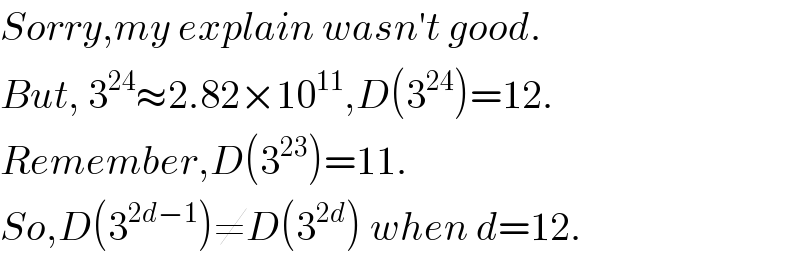
Sorry,my explain wasn′t good. But, 3^(24) ≈2.82×10^(11) ,D(3^(24) )=12. Remember,D(3^(23) )=11. So,D(3^(2d−1) )≠D(3^(2d) ) when d=12.

$${Sorry},{my}\:{explain}\:{wasn}'{t}\:{good}. \\ $$$${But},\:\mathrm{3}^{\mathrm{24}} \approx\mathrm{2}.\mathrm{82}×\mathrm{10}^{\mathrm{11}} ,{D}\left(\mathrm{3}^{\mathrm{24}} \right)=\mathrm{12}. \\ $$$${Remember},{D}\left(\mathrm{3}^{\mathrm{23}} \right)=\mathrm{11}. \\ $$$${So},{D}\left(\mathrm{3}^{\mathrm{2}{d}−\mathrm{1}} \right)\neq{D}\left(\mathrm{3}^{\mathrm{2}{d}} \right)\:{when}\:{d}=\mathrm{12}. \\ $$

Commented by Rasheed Soomro last updated on 04/Aug/16

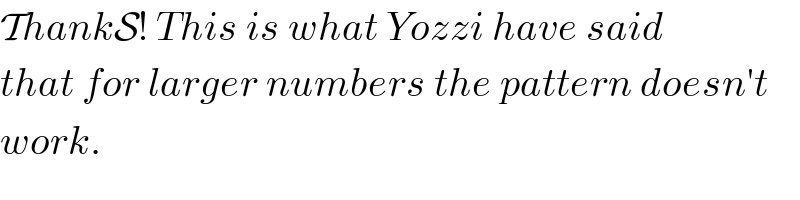
ThankS! This is what Yozzi have said that for larger numbers the pattern doesn′t work.

$$\mathcal{T}{hank}\mathcal{S}!\:{This}\:{is}\:{what}\:{Yozzi}\:{have}\:{said} \\ $$$${that}\:{for}\:{larger}\:{numbers}\:{the}\:{pattern}\:{doesn}'{t} \\ $$$${work}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com