
Question Number 71170 by mr W last updated on 12/Oct/19

Commented by mr W last updated on 12/Oct/19

$${Question}\:#\mathrm{49583}\:\left({reposted}\right) \\ $$$${in}\:{a}\:{paraboloid}\:{cup},\:{which}\:{is}\:{absolutely} \\ $$$${smooth},\:{a}\:{stick}\:{remains}\:{in}\:{equilibrium} \\ $$$${as}\:{shown}.\:{find}\:{the}\:{maximum}\:{length} \\ $$$${the}\:{stick}\:{may}\:{have}. \\ $$
Answered by mr W last updated on 12/Oct/19

Commented by mr W last updated on 01/Dec/19
![let′s say the stick touches the inside of the cup at point A(−e,f). such that the stick is in equilibrium, the contact forces F and N as well as the gravity force of the stick must intersect at the same point S. let η=(h/R), ε=(e/R), λ=(l/R) eqn. of parabola: y=((hx^2 )/R^2 )=((ηx^2 )/R) y′=((2ηx)/R) at A(−e,f): f=((ηe^2 )/R)=ηε^2 R y′=−(1/(tan ϕ))=−((2ηe)/R)=−2ηε ⇒tan ϕ=(1/(2ηε)) point B(R,h): tan θ=((h−f)/(R+e))=((h−ηε^2 R)/(R+e))=((η(1−ε^2 ))/(1+ε))=η(1−ε) eqn. of line AS: ((y−f)/(x+e))=tan ϕ=(1/(2ηε)) ⇒y=f+((x+e)/(2ηε)) eqn. of line SB: ((y−h)/(x−R))=−(1/(tan θ))=−(1/(η(1−ε))) ⇒y=h−((x−R)/(η(1−ε))) point S(x_S ,y_S ): y_S =f+((x_S +e)/(2ηε))=h−((x_S −R)/(η(1−ε))) ηε^2 R+((x_S +e)/(2ηε))=h−((x_S −R)/(η(1−ε))) ηε^2 +(((x_S /R)+ε)/(2ηε))=η−(((x_S /R)−1)/(η(1−ε))) let s=(x_S /R) ηε^2 +((s+ε)/(2ηε))=η−((s−1)/(η(1−ε))) ((s+ε)/(2ε))+((s−1)/(1−ε))=η^2 (1−ε^2 ) ((s−ε)/(2ε(1−ε)))=η^2 (1−ε) ⇒s=ε+2η^2 ε(1−ε)^2 x_S =x_D =−e+((l cos θ)/2)=−e+(l/(2(√(1+tan^2 θ)))) s=(x_S /R)=−ε+(λ/(2(√(1+η^2 (1−ε)^2 )))) −ε+(λ/(2(√(1+η^2 (1−ε)^2 ))))=ε+2η^2 ε(1−ε)^2 ⇒λ=4ε[1+η^2 (1−ε)^2 ]^(3/2) for the maximum of length l, (dλ/dε)=4[1+η^2 (1−ε)^2 ]^(3/2) +4ε(3/2)[1+η^2 (1−ε)^2 ]^(1/2) (−2εη^2 )=0 1+η^2 (1−ε)^2 −3η^2 ε(1−ε)=0 4ε^2 −5ε+1+(1/η^2 )=0 ⇒ε=(1/8)(5−(√(9−((16)/η^2 )))) ⇒λ_(max) =(1/2)(5−(√(9−((16)/η^2 ))))[1+(η^2 /(64))(3+(√(9−((16)/η^2 ))))]^(3/2) ≥4 for η≤1.5242, λ_(max) =4](Q71180.png)
$${let}'{s}\:{say}\:{the}\:{stick}\:{touches}\:{the}\:{inside} \\ $$$${of}\:{the}\:{cup}\:{at}\:{point}\:{A}\left(−{e},{f}\right). \\ $$$${such}\:{that}\:{the}\:{stick}\:{is}\:{in}\:{equilibrium}, \\ $$$${the}\:{contact}\:{forces}\:{F}\:{and}\:{N}\:{as}\:{well}\:{as} \\ $$$${the}\:{gravity}\:{force}\:{of}\:{the}\:{stick}\:{must} \\ $$$${intersect}\:{at}\:{the}\:{same}\:{point}\:{S}. \\ $$$${let}\:\eta=\frac{{h}}{{R}},\:\epsilon=\frac{{e}}{{R}},\:\lambda=\frac{{l}}{{R}} \\ $$$${eqn}.\:{of}\:{parabola}: \\ $$$${y}=\frac{{hx}^{\mathrm{2}} }{{R}^{\mathrm{2}} }=\frac{\eta{x}^{\mathrm{2}} }{{R}} \\ $$$${y}'=\frac{\mathrm{2}\eta{x}}{{R}} \\ $$$${at}\:{A}\left(−{e},{f}\right): \\ $$$${f}=\frac{\eta{e}^{\mathrm{2}} }{{R}}=\eta\epsilon^{\mathrm{2}} {R} \\ $$$${y}'=−\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}=−\frac{\mathrm{2}\eta{e}}{{R}}=−\mathrm{2}\eta\epsilon \\ $$$$\Rightarrow\mathrm{tan}\:\varphi=\frac{\mathrm{1}}{\mathrm{2}\eta\epsilon} \\ $$$${point}\:{B}\left({R},{h}\right): \\ $$$$\mathrm{tan}\:\theta=\frac{{h}−{f}}{{R}+{e}}=\frac{{h}−\eta\epsilon^{\mathrm{2}} {R}}{{R}+{e}}=\frac{\eta\left(\mathrm{1}−\epsilon^{\mathrm{2}} \right)}{\mathrm{1}+\epsilon}=\eta\left(\mathrm{1}−\epsilon\right) \\ $$$${eqn}.\:{of}\:{line}\:{AS}: \\ $$$$\frac{{y}−{f}}{{x}+{e}}=\mathrm{tan}\:\varphi=\frac{\mathrm{1}}{\mathrm{2}\eta\epsilon} \\ $$$$\Rightarrow{y}={f}+\frac{{x}+{e}}{\mathrm{2}\eta\epsilon} \\ $$$${eqn}.\:{of}\:{line}\:{SB}: \\ $$$$\frac{{y}−{h}}{{x}−{R}}=−\frac{\mathrm{1}}{\mathrm{tan}\:\theta}=−\frac{\mathrm{1}}{\eta\left(\mathrm{1}−\epsilon\right)} \\ $$$$\Rightarrow{y}={h}−\frac{{x}−{R}}{\eta\left(\mathrm{1}−\epsilon\right)} \\ $$$${point}\:{S}\left({x}_{{S}} ,{y}_{{S}} \right): \\ $$$${y}_{{S}} ={f}+\frac{{x}_{{S}} +{e}}{\mathrm{2}\eta\epsilon}={h}−\frac{{x}_{{S}} −{R}}{\eta\left(\mathrm{1}−\epsilon\right)} \\ $$$$\eta\epsilon^{\mathrm{2}} {R}+\frac{{x}_{{S}} +{e}}{\mathrm{2}\eta\epsilon}={h}−\frac{{x}_{{S}} −{R}}{\eta\left(\mathrm{1}−\epsilon\right)} \\ $$$$\eta\epsilon^{\mathrm{2}} +\frac{\frac{{x}_{{S}} }{{R}}+\epsilon}{\mathrm{2}\eta\epsilon}=\eta−\frac{\frac{{x}_{{S}} }{{R}}−\mathrm{1}}{\eta\left(\mathrm{1}−\epsilon\right)} \\ $$$${let}\:{s}=\frac{{x}_{{S}} }{{R}} \\ $$$$\eta\epsilon^{\mathrm{2}} +\frac{{s}+\epsilon}{\mathrm{2}\eta\epsilon}=\eta−\frac{{s}−\mathrm{1}}{\eta\left(\mathrm{1}−\epsilon\right)} \\ $$$$\frac{{s}+\epsilon}{\mathrm{2}\epsilon}+\frac{{s}−\mathrm{1}}{\mathrm{1}−\epsilon}=\eta^{\mathrm{2}} \left(\mathrm{1}−\epsilon^{\mathrm{2}} \right) \\ $$$$\frac{{s}−\epsilon}{\mathrm{2}\epsilon\left(\mathrm{1}−\epsilon\right)}=\eta^{\mathrm{2}} \left(\mathrm{1}−\epsilon\right) \\ $$$$\Rightarrow{s}=\epsilon+\mathrm{2}\eta^{\mathrm{2}} \epsilon\left(\mathrm{1}−\epsilon\right)^{\mathrm{2}} \\ $$$${x}_{{S}} ={x}_{{D}} =−{e}+\frac{{l}\:\mathrm{cos}\:\theta}{\mathrm{2}}=−{e}+\frac{{l}}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}} \\ $$$${s}=\frac{{x}_{{S}} }{{R}}=−\epsilon+\frac{\lambda}{\mathrm{2}\sqrt{\mathrm{1}+\eta^{\mathrm{2}} \left(\mathrm{1}−\epsilon\right)^{\mathrm{2}} }} \\ $$$$−\epsilon+\frac{\lambda}{\mathrm{2}\sqrt{\mathrm{1}+\eta^{\mathrm{2}} \left(\mathrm{1}−\epsilon\right)^{\mathrm{2}} }}=\epsilon+\mathrm{2}\eta^{\mathrm{2}} \epsilon\left(\mathrm{1}−\epsilon\right)^{\mathrm{2}} \\ $$$$\Rightarrow\lambda=\mathrm{4}\epsilon\left[\mathrm{1}+\eta^{\mathrm{2}} \left(\mathrm{1}−\epsilon\right)^{\mathrm{2}} \right]^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$ \\ $$$${for}\:{the}\:{maximum}\:{of}\:{length}\:{l}, \\ $$$$\frac{{d}\lambda}{{d}\epsilon}=\mathrm{4}\left[\mathrm{1}+\eta^{\mathrm{2}} \left(\mathrm{1}−\epsilon\right)^{\mathrm{2}} \right]^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{4}\epsilon\frac{\mathrm{3}}{\mathrm{2}}\left[\mathrm{1}+\eta^{\mathrm{2}} \left(\mathrm{1}−\epsilon\right)^{\mathrm{2}} \right]^{\frac{\mathrm{1}}{\mathrm{2}}} \left(−\mathrm{2}\epsilon\eta^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{1}+\eta^{\mathrm{2}} \left(\mathrm{1}−\epsilon\right)^{\mathrm{2}} −\mathrm{3}\eta^{\mathrm{2}} \epsilon\left(\mathrm{1}−\epsilon\right)=\mathrm{0} \\ $$$$\mathrm{4}\epsilon^{\mathrm{2}} −\mathrm{5}\epsilon+\mathrm{1}+\frac{\mathrm{1}}{\eta^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\epsilon=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{5}−\sqrt{\mathrm{9}−\frac{\mathrm{16}}{\eta^{\mathrm{2}} }}\right) \\ $$$$\Rightarrow\lambda_{{max}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{5}−\sqrt{\mathrm{9}−\frac{\mathrm{16}}{\eta^{\mathrm{2}} }}\right)\left[\mathrm{1}+\frac{\eta^{\mathrm{2}} }{\mathrm{64}}\left(\mathrm{3}+\sqrt{\mathrm{9}−\frac{\mathrm{16}}{\eta^{\mathrm{2}} }}\right)\right]^{\frac{\mathrm{3}}{\mathrm{2}}} \geqslant\mathrm{4} \\ $$$$ \\ $$$${for}\:\eta\leqslant\mathrm{1}.\mathrm{5242},\:\lambda_{{max}} =\mathrm{4} \\ $$
Commented by ajfour last updated on 12/Oct/19
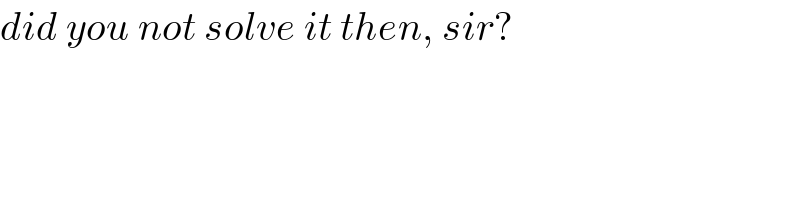
$${did}\:{you}\:{not}\:{solve}\:{it}\:{then},\:{sir}? \\ $$
Commented by mr W last updated on 12/Oct/19

Commented by mr W last updated on 12/Oct/19

$${sir},\:{i}\:{deleted}\:{the}\:{old}\:{post}\:{by}\:{accident},\: \\ $$$${but}\:{i}\:{wanted}\:{to}\:{keep}\:{the}\:{solution} \\ $$$${somehow},\:{therefore}\:{i}\:{reposted}\:{it}\:{here}. \\ $$
Commented by mr W last updated on 12/Oct/19

Commented by mr W last updated on 12/Oct/19

