
Question Number 74040 by Learner-123 last updated on 18/Nov/19
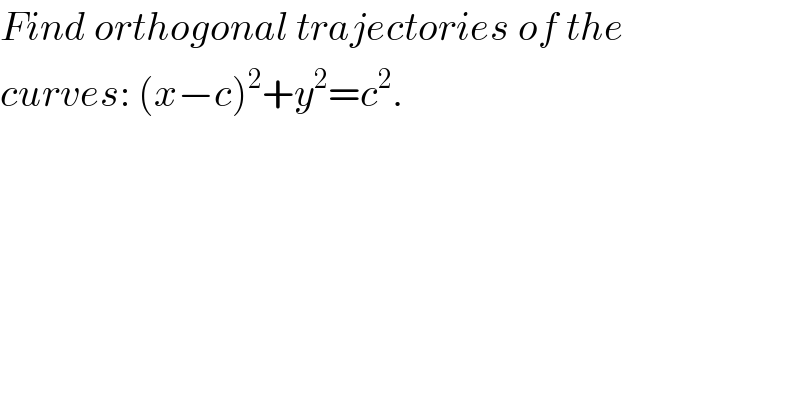
$${Find}\:{orthogonal}\:{trajectories}\:{of}\:{the} \\ $$$${curves}:\:\left({x}−{c}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={c}^{\mathrm{2}} . \\ $$
Commented by Learner-123 last updated on 18/Nov/19

$${please}\:{help}... \\ $$
Answered by mind is power last updated on 18/Nov/19

$$\Leftrightarrow{x}^{\mathrm{2}} −\mathrm{2}{cx}+{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Gamma_{{c}\:\:\:} {bee}\:{this}\:{family}\:{of}\:{curves} \\ $$$$\Rightarrow\frac{\partial}{\partial{x}}\left({x}^{\mathrm{2}} −\mathrm{2}{cx}+{y}^{\mathrm{2}} \right)=\mathrm{0}=\mathrm{2}{x}−\mathrm{2}{c}+\mathrm{2}\frac{{dy}}{{dx}}{y}=\mathrm{0} \\ $$$$\Rightarrow{x}−{c}+\frac{{dy}}{{dx}}.{y}=\mathrm{0}...{E} \\ $$$$\:\frac{{dy}}{{dx}}\:\:{is}\:{direction}\:{coeficent}\:{of}\:{tangent}\:{in}\:{M}\left({x},{y}\right) \\ $$$${in}\:{orthogonal}\:{trajectories} \\ $$$${tangentwill}\:{bee}\:{ortogonal} \\ $$$$\Gamma'_{{c}} \:\:{irthogonal}\:{trajectories}\:{of}\:\Gamma_{{c}} \\ $$$${M}\left({x},{S}\right)\in\Gamma'\:\Rightarrow{tangent}\:{is}\:{M}\:{hase}\:{director}\:{coeficient} \\ $$$$\frac{{dY}}{{dx}}.\frac{{dy}}{{dx}}=−\mathrm{1}\Rightarrow\frac{{dy}}{{dx}}=\frac{−{dx}}{{dY}} \\ $$$$\Leftrightarrow{E}\:\:{x}−{c}−\frac{{dx}}{{dY}}.{Y}=\mathrm{0}\Leftrightarrow\frac{{dY}}{{Y}}=\frac{{dx}}{{x}−{c}}\Rightarrow{ln}\mid{Y}\mid={k}\left({x}−{c}\right) \\ $$$$\Rightarrow{Y}={k}\left({x}−{c}\right)\:{lign} \\ $$
Commented by Learner-123 last updated on 19/Nov/19
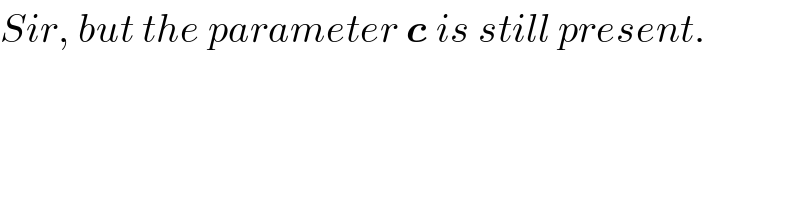
$${Sir},\:{but}\:{the}\:{parameter}\:\boldsymbol{{c}}\:{is}\:{still}\:{present}. \\ $$
Commented by mind is power last updated on 19/Nov/19
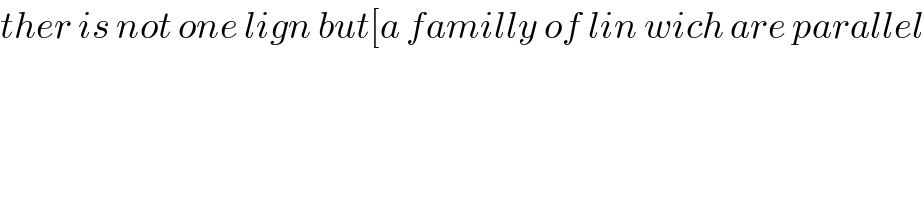
$${ther}\:{is}\:{not}\:{one}\:{lign}\:{but}\left[{a}\:{familly}\:{of}\:{lin}\:{wich}\:{are}\:{parallel}\right. \\ $$
Commented by Learner-123 last updated on 19/Nov/19

$${thanks}\:{sir}. \\ $$
