
Question Number 74087 by mr W last updated on 19/Nov/19
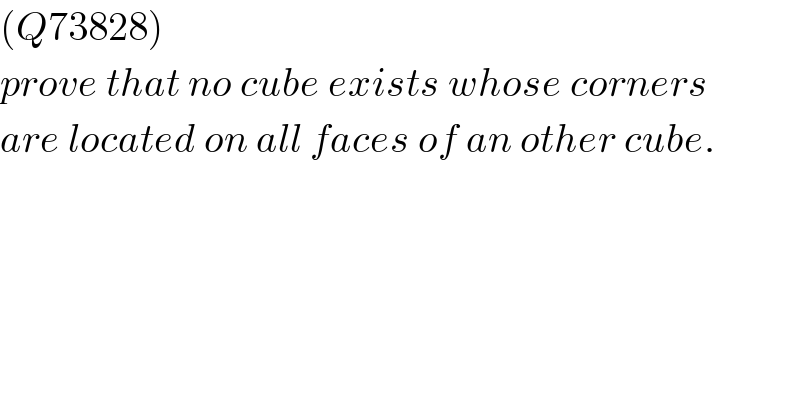
$$\left({Q}\mathrm{73828}\right) \\ $$$${prove}\:{that}\:{no}\:{cube}\:{exists}\:{whose}\:{corners} \\ $$$${are}\:{located}\:{on}\:{all}\:{faces}\:{of}\:{an}\:{other}\:{cube}. \\ $$
Commented by mr W last updated on 18/Nov/19

$${here}\:{is}\:{my}\:{proof}: \\ $$$${the}\:{inner}\:{cube}\:{has}\:\mathrm{8}\:{corners},\:{but}\:{the} \\ $$$${outer}\:{cubes}\:{has}\:{only}\:\mathrm{6}\:{faces}. \\ $$$${that}\:{means}\:{two}\:{of} \\ $$$${its}\:{corners}\:{must}\:{lie}\:{on}\:{the}\:{same}\:{face} \\ $$$${of}\:{the}\:{outer}\:{cube}.\:{say}\:{these}\:{two}\:{corners} \\ $$$${of}\:{the}\:{inner}\:{cube}\:{are}\:\mathrm{1}\:{and}\:\mathrm{2}.\:{they}\:{lie} \\ $$$${on}\:{the}\:{face}\:{ABCD}\:{of}\:{the}\:{outer}\:{cube}. \\ $$
Commented by ajfour last updated on 18/Nov/19

$${think}\:{over}\:{sir}-\:{it}\:{shouldn}'{t}\: \\ $$$${mean}\:{that}.\:\left({question}\:\:{said}\:{on}\:{each}\:\right. \\ $$$${face}\:{of}\:{outer}\:{cube}\:{there}\:{is}\:{an}\:{inner} \\ $$$$\left.{cube}'{s}\:{corner}\right)\:\:\: \\ $$$${later}\:{i}\:{added}\:{at}\:{least},\:{still}\:{two} \\ $$$${corners}\:{may}\:{or}\:{maynot}\:{touch} \\ $$$${the}\:{outer}\:{cube}\:{walls}.. \\ $$
Commented by mr W last updated on 18/Nov/19
Commented by mr W last updated on 18/Nov/19

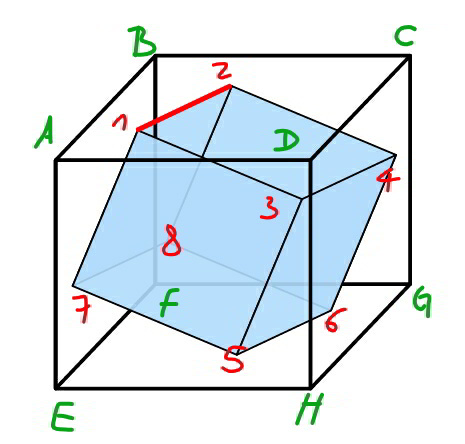
$${so}\:{we}\:{have}\:{an}\:{edge}\:\mathrm{12}\:{from}\:{the}\:{inner} \\ $$$${cube}\:{in}\:{the}\:{plane}\:{ABCD}. \\ $$$${other}\:{corners}\:{of}\:{the}\:{inner}\:{cube}\:{are} \\ $$$${numbered}\:{as}\:{shown}. \\ $$$${we}\:{know}\:{these}\:{edges}\:{are}\:{parallel}: \\ $$$$\mathrm{34}//\mathrm{56}//\mathrm{78}//\mathrm{12}. \\ $$$${their}\:{projections}\:{in}\:{the}\:{plane}\:{EFGH} \\ $$$${are}\:{also}\:{parallel}. \\ $$$${it}'{s}\:{easy}\:{to}\:{see}\:{that}\:{the}\:{edge}\:\mathrm{56}\:{must} \\ $$$${lie}\:{in}\:{the}\:{opposite}\:{face}\:{EFGH}\:{from} \\ $$$${the}\:{outer}\:{cube}.\:\left({but}\:{this}\:{is}\:{not}\:{relevant}\right. \\ $$$$\left.{for}\:{the}\:{proof}.\right) \\ $$$${face}\:\mathrm{2468}\:{and}\:{face}\:\mathrm{1357}\:{from}\:{the} \\ $$$${inner}\:{cube}\:{are}\:{perpendicular}\:{to}\:{the} \\ $$$${edge}\:\mathrm{12}.\:\left({clear}\right) \\ $$$${let}'{s}\:{image}\:{that}\:{we}\:{cut}\:{the}\:{outer}\:{cube} \\ $$$${along}\:{these}\:{two}\:{faces}\:{from}\:{the}\:{inner} \\ $$$${cube}.\:{both}\:{cut}\:{sections}\:{are}\:{perpendicular} \\ $$$${to}\:{the}\:{face}\:{ABCD}\:{and}\:{EFGH}. \\ $$$${the}\:{shape}\:{of}\:{both}\:{cut}\:{sections}\:{is} \\ $$$${rectangle}. \\ $$
Commented by ajfour last updated on 18/Nov/19

$${but}\:{Sir}\:{i}\:{believe}\:{that}\:{two}\:{left} \\ $$$${out}\:{corners}\:{can}\:{just}\:{be}\:{inside} \\ $$$${and}\:{not}\:{touch}\:{the}\:{outer}\:{cube}, \\ $$$${such}\:{an}\:{orientation},\:{might}\:{even} \\ $$$${result}...\left({here}\:\mathrm{2}\:{can}\:{be}\:{bit}\:{below}\right. \\ $$$${the}\:{ceiling}\:{and}\:\mathrm{5}\:{slightly}\:{above} \\ $$$${the}\:{floor}\:.. \\ $$
Commented by mr W last updated on 18/Nov/19
Commented by mr W last updated on 18/Nov/19

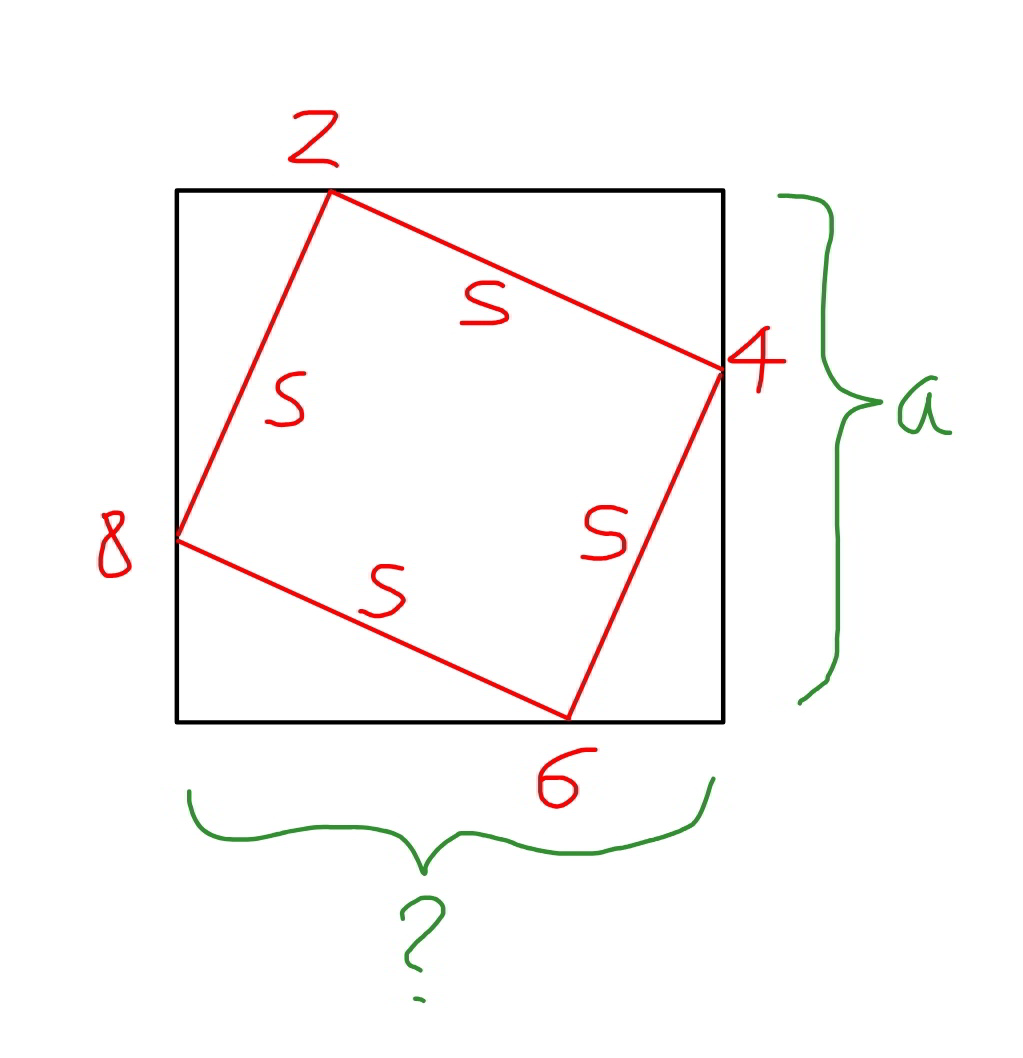
$${since}\:{the}\:{face}\:\mathrm{2468}\:{is}\:{an}\:{inscribed} \\ $$$${square}\:{of}\:{the}\:{rectangle},\:{the}\:{rectangle} \\ $$$${must}\:{be}\:{also}\:{a}\:{square}\:{with}\:{side}\:{length}\:{a}. \\ $$$${that}\:{means}\:{the}\:{both}\:{cut}\:{sections}\:{must} \\ $$$${be}\:{of}\:{same}\:{size}. \\ $$
Commented by mr W last updated on 18/Nov/19
Commented by mr W last updated on 18/Nov/19

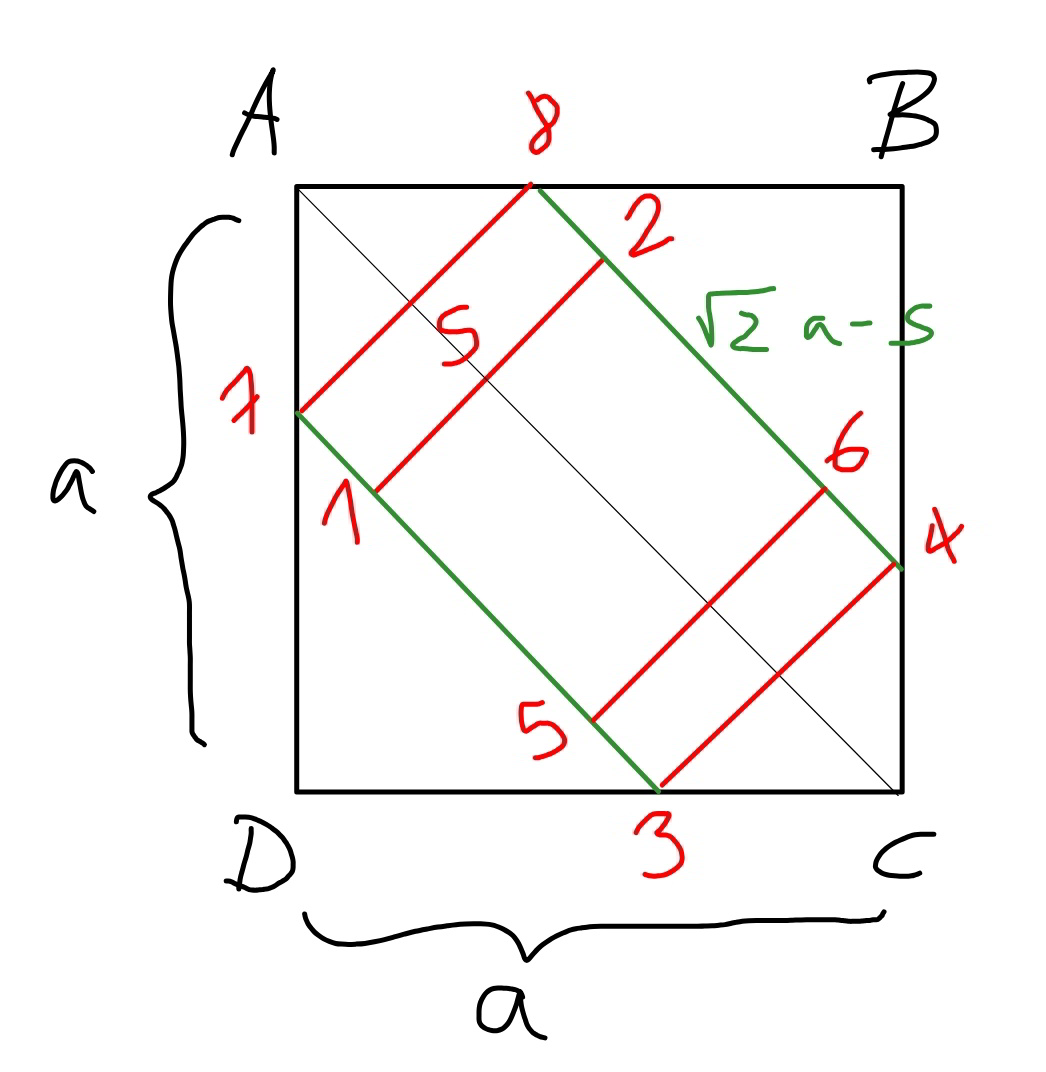
$${we}\:{get}\:{the}\:{length}\:{of}\:{the}\:{cut}\:{section}\:{of} \\ $$$$\sqrt{\mathrm{2}}{a}−{s}\:{and}\:{heigth}\:{of}\:{a}. \\ $$$$\sqrt{\mathrm{2}}{a}−{s}={a} \\ $$$$\Rightarrow{s}=\left(\sqrt{\mathrm{2}}−\mathrm{1}\right){a}\:\:\:...\left({i}\right) \\ $$$${since}\:{square}\:{of}\:{length}\:{s}\:{is}\:{an}\:{inscribed} \\ $$$${square}\:{of}\:{the}\:{square}\:{with}\:{side}\:{length}\:{a}, \\ $$$${s}\geqslant\frac{{a}}{\sqrt{\mathrm{2}}}\:\:\:\:...\left({ii}\right) \\ $$$${we}\:{can}\:{not}\:{find}\:{a}\:{value}\:{of}\:{s}\:{which} \\ $$$${fulfills}\:{both}\:\left({i}\right)\:{and}\:\left({ii}\right). \\ $$$${that}\:{means}\:{an}\:{inner}\:{cube}\:{doesn}'{t} \\ $$$${exist}\:{which}\:{touches}\:{all}\:\mathrm{6}\:{faces}\:{of}\:{an} \\ $$$${other}\:{cube}. \\ $$
Commented by ajfour last updated on 18/Nov/19
$${you}\:{might}\:{not}\:{be}\:{correct}\:{here}\:{Sir}, \\ $$$${when}\:{you}\:{believe}- \\ $$$$''{if}\:{such}\:{an}\:{inner}\:{cube}\:{exists},\:{two}\:{of} \\ $$$${its}\:{corners}\:{must}\:{lie}\:{on}\:{the}\:{same}\:{face} \\ $$$${of}\:{the}\:{outer}\:{cube}.'' \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 18/Nov/19

$${ajfour}\:{sir}: \\ $$$${the}\:{original}\:{question}\:{requested}\:{that} \\ $$$${on}\:{each}\:{of}\:{the}\:\mathrm{6}\:{faces}\:{of}\:{larger}\:{cube} \\ $$$${there}\:{is}\:{at}\:{least}\:{one}\:{corner}\:{from}\:{the} \\ $$$${inner}\:{cube}.\:{that}\:{means}\:{the}\:\mathrm{8}\:{corners} \\ $$$${of}\:{the}\:{inner}\:{cube}\:{must}\:{touch}\:{all}\:\mathrm{6} \\ $$$${faces}\:{of}\:{the}\:{outer}\:{cube}. \\ $$
Commented by mr W last updated on 18/Nov/19

$${if}\:{not}\:{all}\:{corners}\:{of}\:{the}\:{inner}\:{cube} \\ $$$${should}\:{be}\:{on}\:{the}\:{faces}\:{of}\:{the}\:{outer} \\ $$$${cube},\:{the}\:{situation}\:{is}\:{quite}\:{different}. \\ $$
Commented by ajfour last updated on 18/Nov/19

$${let}\:{us}\:{not}\:{be}\:{deceived}\:{by}\:{the} \\ $$$${lack}\:{of}\:{clarity}\:{in}\:{diagram}, \\ $$$${and}\:{instead}\:{focus}\:{on}\:{how}\:{the} \\ $$$${question}\:{is}\:{worded},\:{let}\:{us}\:{both} \\ $$$${review}\:{it}\:{and}\:{Sir}\:{please}\:{see}\:{the} \\ $$$${diagram}\:{believing}\:{that}\:\mathrm{2}\:{is}\:{below} \\ $$$${ceiling}\:{and}\:{not}\:{touching}\:{the} \\ $$$${back}\:{face}/{wall}\:{and}\:{at}\:{the}\:{same} \\ $$$${time}\:\mathrm{5}\:{is}\:{above}\:{the}\:{floor},\:{and} \\ $$$${not}\:{touching}\:{the}\:{front}\:{face}; \\ $$$$\left({this}\:{orientation}\:{even}\:{might}\right. \\ $$$${not}\:{exist}\:{but}\:{until}\:{it}\:{is}\:{proved} \\ $$$${with}\:{analysis},\:{i}\:{imagined}\:{this} \\ $$$${was}\:{possible}\:{with}\:{a}\:{little}\:{range} \\ $$$${of}\:{values}\:{of}\:\boldsymbol{{s}}.\:{Hence}\:{asked}\:{for} \\ $$$$\boldsymbol{{s}}_{{min}} . \\ $$
Commented by ajfour last updated on 18/Nov/19

$${the}\:{situation}\:{is}\:{quite}\:{different}/ \\ $$$${much}\:{interesting}\:{then},\:{thank} \\ $$$${you}\:{Sir},\:{my}\:{solution}\:{attempt} \\ $$$${is}\:{split}\:{in}\:{two}\:{posts}.\:{First} \\ $$$${in}\:{the}\:{original}\:{question},\:{and} \\ $$$${then}\:{in}\:{a}\:{later}\:{post}\:{as}\:{a}\:{system} \\ $$$${of}\:{simultaneous}\:{equations}, \\ $$$$\left({Q}.\mathrm{74024}\right) \\ $$$${please}\:{give}\:{a}\:{glance}\:{Sir}.. \\ $$
Commented by mr W last updated on 19/Nov/19

$${now}\:{i}\:{understand}\:{your}\:{solutions}.\:{yet} \\ $$$${it}'{s}\:{not}\:{easy}\:{to}\:{find}\:{s}. \\ $$
