Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 7472 by FilupSmith last updated on 31/Aug/16

Show why: lim_(x→−∞) x^x = 0

$$\mathrm{Show}\:\mathrm{why}: \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{x}^{{x}} \:=\:\mathrm{0} \\ $$

Commented by FilupSmith last updated on 31/Aug/16

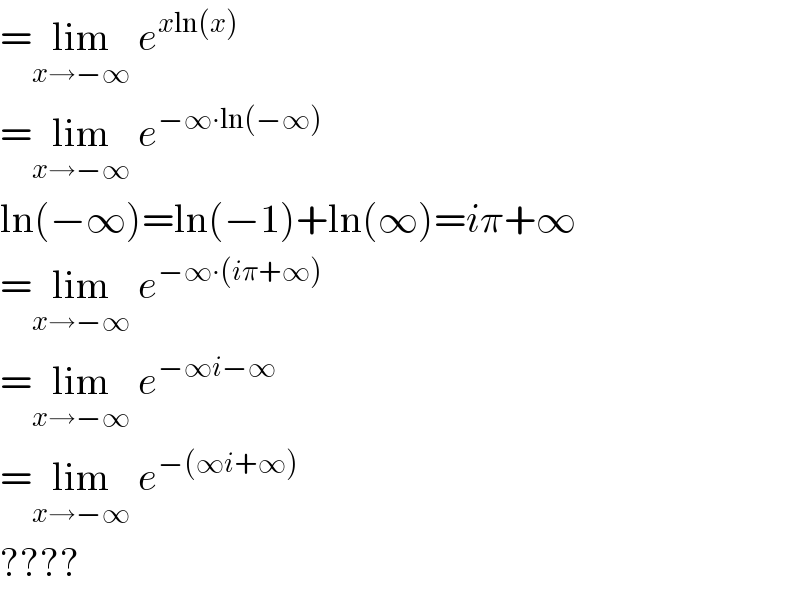
=lim_(x→−∞) e^(xln(x)) =lim_(x→−∞) e^(−∞∙ln(−∞)) ln(−∞)=ln(−1)+ln(∞)=iπ+∞ =lim_(x→−∞) e^(−∞∙(iπ+∞)) =lim_(x→−∞) e^(−∞i−∞) =lim_(x→−∞) e^(−(∞i+∞)) ????

$$=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{e}^{{x}\mathrm{ln}\left({x}\right)} \\ $$$$=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{e}^{−\infty\centerdot\mathrm{ln}\left(−\infty\right)} \\ $$$$\mathrm{ln}\left(−\infty\right)=\mathrm{ln}\left(−\mathrm{1}\right)+\mathrm{ln}\left(\infty\right)={i}\pi+\infty \\ $$$$=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{e}^{−\infty\centerdot\left({i}\pi+\infty\right)} \\ $$$$=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{e}^{−\infty{i}−\infty} \\ $$$$=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{e}^{−\left(\infty{i}+\infty\right)} \\ $$$$???? \\ $$

Answered by Yozzia last updated on 31/Aug/16

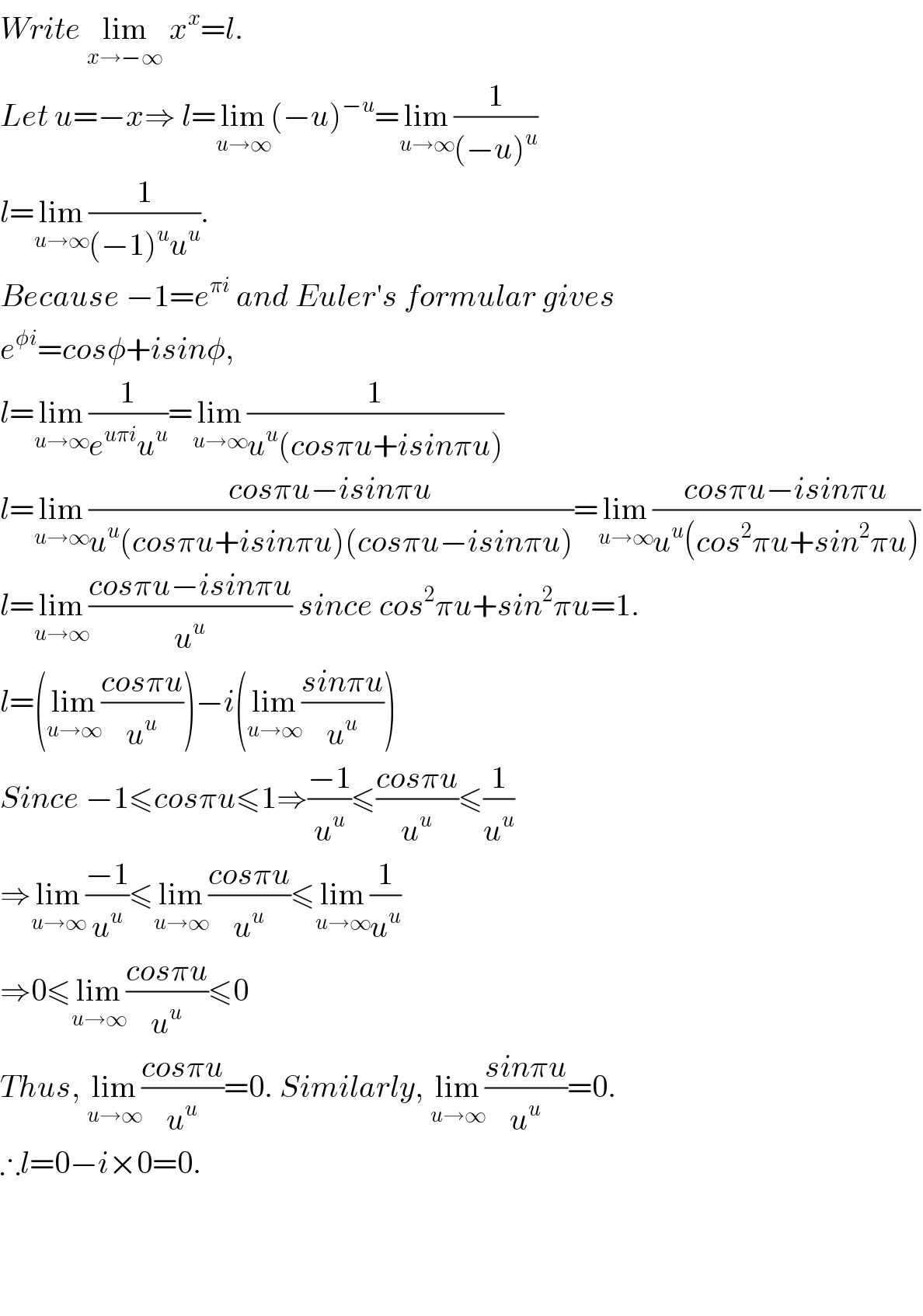
Write lim_(x→−∞) x^x =l. Let u=−x⇒ l=lim_(u→∞) (−u)^(−u) =lim_(u→∞) (1/((−u)^u )) l=lim_(u→∞) (1/((−1)^u u^u )). Because −1=e^(πi) and Euler′s formular gives e^(φi) =cosφ+isinφ, l=lim_(u→∞) (1/(e^(uπi) u^u ))=lim_(u→∞) (1/(u^u (cosπu+isinπu))) l=lim_(u→∞) ((cosπu−isinπu)/(u^u (cosπu+isinπu)(cosπu−isinπu)))=lim_(u→∞) ((cosπu−isinπu)/(u^u (cos^2 πu+sin^2 πu))) l=lim_(u→∞) ((cosπu−isinπu)/u^u ) since cos^2 πu+sin^2 πu=1. l=(lim_(u→∞) ((cosπu)/u^u ))−i(lim_(u→∞) ((sinπu)/u^u )) Since −1≤cosπu≤1⇒((−1)/u^u )≤((cosπu)/u^u )≤(1/u^u ) ⇒lim_(u→∞) ((−1)/u^u )≤lim_(u→∞) ((cosπu)/u^u )≤lim_(u→∞) (1/u^u ) ⇒0≤lim_(u→∞) ((cosπu)/u^u )≤0 Thus, lim_(u→∞) ((cosπu)/u^u )=0. Similarly, lim_(u→∞) ((sinπu)/u^u )=0. ∴l=0−i×0=0.

$${Write}\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{x}^{{x}} ={l}. \\ $$$${Let}\:{u}=−{x}\Rightarrow\:{l}=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\left(−{u}\right)^{−{u}} =\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\left(−{u}\right)^{{u}} } \\ $$$${l}=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\left(−\mathrm{1}\right)^{{u}} {u}^{{u}} }. \\ $$$${Because}\:−\mathrm{1}={e}^{\pi{i}} \:{and}\:{Euler}'{s}\:{formular}\:{gives}\: \\ $$$${e}^{\phi{i}} ={cos}\phi+{isin}\phi, \\ $$$${l}=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{e}^{{u}\pi{i}} {u}^{{u}} }=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{u}^{{u}} \left({cos}\pi{u}+{isin}\pi{u}\right)} \\ $$$${l}=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{{cos}\pi{u}−{isin}\pi{u}}{{u}^{{u}} \left({cos}\pi{u}+{isin}\pi{u}\right)\left({cos}\pi{u}−{isin}\pi{u}\right)}=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{{cos}\pi{u}−{isin}\pi{u}}{{u}^{{u}} \left({cos}^{\mathrm{2}} \pi{u}+{sin}^{\mathrm{2}} \pi{u}\right)} \\ $$$${l}=\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{{cos}\pi{u}−{isin}\pi{u}}{{u}^{{u}} }\:{since}\:{cos}^{\mathrm{2}} \pi{u}+{sin}^{\mathrm{2}} \pi{u}=\mathrm{1}. \\ $$$${l}=\left(\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{{cos}\pi{u}}{{u}^{{u}} }\right)−{i}\left(\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{{sin}\pi{u}}{{u}^{{u}} }\right) \\ $$$${Since}\:−\mathrm{1}\leqslant{cos}\pi{u}\leqslant\mathrm{1}\Rightarrow\frac{−\mathrm{1}}{{u}^{{u}} }\leqslant\frac{{cos}\pi{u}}{{u}^{{u}} }\leqslant\frac{\mathrm{1}}{{u}^{{u}} } \\ $$$$\Rightarrow\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{−\mathrm{1}}{{u}^{{u}} }\leqslant\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{{cos}\pi{u}}{{u}^{{u}} }\leqslant\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{u}^{{u}} } \\ $$$$\Rightarrow\mathrm{0}\leqslant\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{{cos}\pi{u}}{{u}^{{u}} }\leqslant\mathrm{0} \\ $$$${Thus},\:\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{{cos}\pi{u}}{{u}^{{u}} }=\mathrm{0}.\:{Similarly},\:\underset{{u}\rightarrow\infty} {\mathrm{lim}}\frac{{sin}\pi{u}}{{u}^{{u}} }=\mathrm{0}. \\ $$$$\therefore{l}=\mathrm{0}−{i}×\mathrm{0}=\mathrm{0}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by FilupSmith last updated on 01/Sep/16

Amazing!

$$\mathrm{Amazing}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com