
Question Number 7582 by A WLAN last updated on 04/Sep/16

Commented by A WLAN last updated on 04/Sep/16
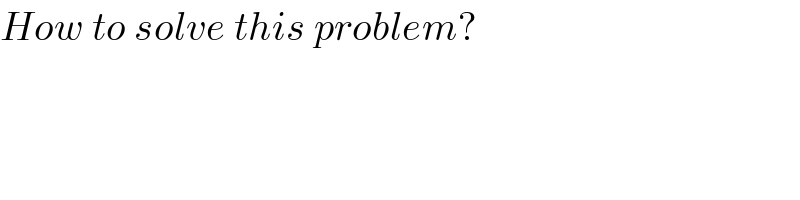
$${How}\:{to}\:{solve}\:{this}\:{problem}? \\ $$
Answered by Yozzia last updated on 04/Sep/16

$${w}=\mathrm{1}/{z}.\:{You}\:{can}\:{plot}\:{the}\:{initial}\:{point}\:{z} \\ $$$${and}\:{the}\:{point}\:{w}\:{on}\:{an}\:{Argand}\:{diagram}\:{to}\:{deduce}\:{the}\:{angle}\:{of} \\ $$$${rotation}. \\ $$$${z}=\mathrm{1}\Rightarrow{w}=\mathrm{1}/\mathrm{1}={z}\Rightarrow\:{angle}\:{of}\:{rotation}\:{is}\:\mathrm{0}°\: \\ $$$${about}\:{the}\:{origin}.\:{z}=\mathrm{1}\:{is}\:{invariant}\:{under}\:{the}\:{transformation}. \\ $$$${z}={i}\Rightarrow{w}=\mathrm{1}/{i}=−{i}=−{z}\Rightarrow\:{angle}\:{of}\:{rotation}\:{is}\:\mathrm{180}°\: \\ $$$${about}\:{the}\:{origin}.\: \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Alternatively},\:{we}\:{can}\:{find}\:{the}\:{argument} \\ $$$${of}\:\frac{{w}}{{z}}.\:{Let}\:{w}={r}_{\mathrm{1}} {e}^{{i}\phi\:} {and}\:{z}={r}_{\mathrm{2}} {e}^{{i}\theta} . \\ $$$$\frac{{w}}{{z}}=\frac{{r}_{\mathrm{1}} }{{r}_{\mathrm{2}} }{e}^{{i}\left(\phi−\theta\right)} \Rightarrow{arg}\left({w}/{z}\right)=\phi−\theta={arg}\left({w}\right)−{arg}\left({z}\right) \\ $$$${For}\:{z}=\mathrm{1}\Rightarrow{arg}\left({z}\right)=\theta={tan}^{−\mathrm{1}} \frac{\mathrm{0}}{\mathrm{1}}=\mathrm{0}\:{radians} \\ $$$$\because\:{w}=\mathrm{1}/{z}\Rightarrow\:{w}=\mathrm{1}\Rightarrow{arg}\left({w}\right)=\phi={tan}^{−\mathrm{1}} \frac{\mathrm{0}}{\mathrm{1}}=\mathrm{0}\:{radians} \\ $$$$\therefore\:{arg}\left({w}/{z}\right)=\mathrm{0}−\mathrm{0}=\mathrm{0}\:{radians}.\: \\ $$$$\Rightarrow{The}\:{angle}\:{between}\:{w}\:{and}\:{z}\:{is}\:\mathrm{0}\:{radians}. \\ $$$$\Rightarrow{The}\:{angle}\:{of}\:{rotation}\:{about}\:{the}\:{origin}\:{is}\:\mathrm{0}\:{radians}. \\ $$$${z}={i}\Rightarrow\:{arg}\left({z}\right)=\theta=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}=\frac{\pi}{\mathrm{2}} \\ $$$${w}=\mathrm{1}/{z}=\mathrm{1}/{i}=−{i}\Rightarrow\:{arg}\left({w}\right)=\phi=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}{tan}\frac{−\mathrm{1}}{{x}}=−\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}=\frac{−\pi}{\mathrm{2}} \\ $$$$\therefore\:{arg}\left({w}/{z}\right)=\frac{−\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}=−\pi. \\ $$$$\Rightarrow\:{The}\:{angle}\:{between}\:{w}\:{and}\:{z}\:{is}\:\pi\:{radians}. \\ $$$$\Rightarrow{The}\:{angle}\:{of}\:{rotation}\:{is}\:\pi\:{radians}\:{about}\:{the}\:{origin}. \\ $$$$ \\ $$
