Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 76657 by Tony Lin last updated on 29/Dec/19

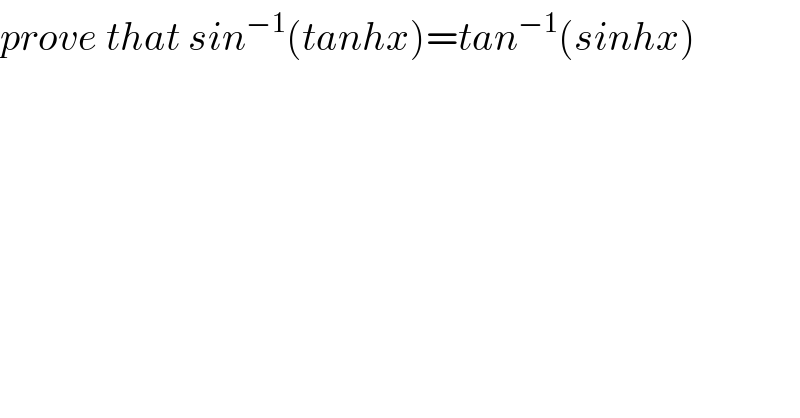
prove that sin^(−1) (tanhx)=tan^(−1) (sinhx)

$${prove}\:{that}\:{sin}^{−\mathrm{1}} \left({tanhx}\right)={tan}^{−\mathrm{1}} \left({sinhx}\right) \\ $$

Answered by john santu last updated on 29/Dec/19

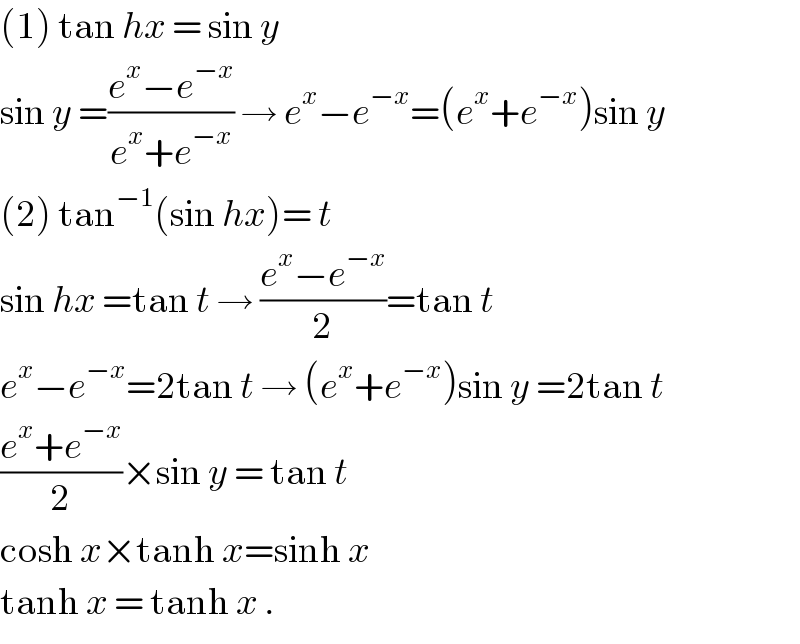
(1) tan hx = sin y sin y =((e^x −e^(−x) )/(e^x +e^(−x) )) → e^x −e^(−x) =(e^x +e^(−x) )sin y (2) tan^(−1) (sin hx)= t sin hx =tan t → ((e^x −e^(−x) )/2)=tan t e^x −e^(−x) =2tan t → (e^x +e^(−x) )sin y =2tan t ((e^x +e^(−x) )/2)×sin y = tan t cosh x×tanh x=sinh x tanh x = tanh x .

$$\left(\mathrm{1}\right)\:\mathrm{tan}\:{hx}\:=\:\mathrm{sin}\:{y} \\ $$$$\mathrm{sin}\:{y}\:=\frac{{e}^{{x}} −{e}^{−{x}} }{{e}^{{x}} +{e}^{−{x}} }\:\rightarrow\:{e}^{{x}} −{e}^{−{x}} =\left({e}^{{x}} +{e}^{−{x}} \right)\mathrm{sin}\:{y} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{sin}\:{hx}\right)=\:{t} \\ $$$$\mathrm{sin}\:{hx}\:=\mathrm{tan}\:{t}\:\rightarrow\:\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}}=\mathrm{tan}\:{t} \\ $$$${e}^{{x}} −{e}^{−{x}} =\mathrm{2tan}\:{t}\:\rightarrow\:\left({e}^{{x}} +{e}^{−{x}} \right)\mathrm{sin}\:{y}\:=\mathrm{2tan}\:{t} \\ $$$$\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}}×\mathrm{sin}\:{y}\:=\:\mathrm{tan}\:{t} \\ $$$$\mathrm{cosh}\:{x}×\mathrm{tanh}\:{x}=\mathrm{sinh}\:{x}\: \\ $$$$\mathrm{tanh}\:{x}\:=\:\mathrm{tanh}\:{x}\:. \\ $$

Commented by mr W last updated on 29/Dec/19

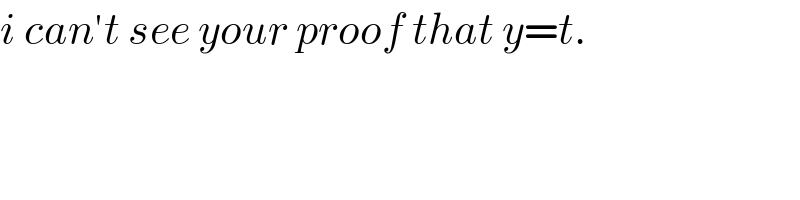
i can′t see your proof that y=t.

$${i}\:{can}'{t}\:{see}\:{your}\:{proof}\:{that}\:{y}={t}. \\ $$

Commented by john santu last updated on 29/Dec/19

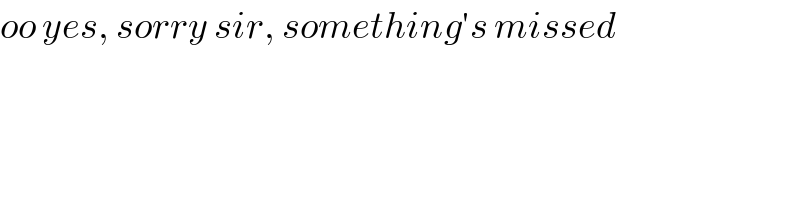
oo yes, sorry sir, something′s missed

$${oo}\:{yes},\:{sorry}\:{sir},\:{something}'{s}\:{missed} \\ $$

Answered by mr W last updated on 29/Dec/19

let LHS=sin^(−1) (tanhx)=u ⇒tanh x=sin u ⇒((sinh x)/(cosh x))=sin u ⇒((sinh^2 x)/(cosh^2 x))=sin^2 u ⇒((sinh^2 x)/(1+sinh^2 x))=sin^2 u ⇒sinh^2 x=((sin^2 u)/(1−sin^2 u))=((sin^2 u)/(cos^2 u))=tan^2 u ⇒sinh x=tan u ⇒tan^(−1) (sinh x)=u ⇒tan^(−1) (sinh x)=sin^(−1) (tanhx)

$${let}\:{LHS}={sin}^{−\mathrm{1}} \left({tanhx}\right)={u} \\ $$$$\Rightarrow\mathrm{tanh}\:{x}=\mathrm{sin}\:{u} \\ $$$$\Rightarrow\frac{\mathrm{sinh}\:{x}}{\mathrm{cosh}\:{x}}=\mathrm{sin}\:{u} \\ $$$$\Rightarrow\frac{\mathrm{sinh}^{\mathrm{2}} \:{x}}{\mathrm{cosh}^{\mathrm{2}} \:{x}}=\mathrm{sin}^{\mathrm{2}} \:{u} \\ $$$$\Rightarrow\frac{\mathrm{sinh}^{\mathrm{2}} \:{x}}{\mathrm{1}+\mathrm{sinh}^{\mathrm{2}} \:{x}}=\mathrm{sin}^{\mathrm{2}} \:{u} \\ $$$$\Rightarrow\mathrm{sinh}^{\mathrm{2}} \:{x}=\frac{\mathrm{sin}^{\mathrm{2}} \:{u}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{u}}=\frac{\mathrm{sin}^{\mathrm{2}} \:{u}}{\mathrm{cos}^{\mathrm{2}} \:{u}}=\mathrm{tan}^{\mathrm{2}} \:{u} \\ $$$$\Rightarrow\mathrm{sinh}\:{x}=\mathrm{tan}\:{u} \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{sinh}\:{x}\right)={u} \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{sinh}\:{x}\right)={sin}^{−\mathrm{1}} \left({tanhx}\right) \\ $$

Commented by Tony Lin last updated on 29/Dec/19

thank you both

$${thank}\:{you}\:{both} \\ $$

Answered by mind is power last updated on 29/Dec/19

Hello happy too back withe you Since th(x) is bijection ]−∞,+∞[−{0}→]−1,1[ ⇒∀u∈]−1,+1[,∃!x∈R^∗ ∣u=th(x) sin^− (th(x))=sin^− (u) tan^− (sh(x))=tan^− (sh(th^− (u))) th(u)=((sh(u))/(ch(u))) ch^2 −sh^2 =1⇒ sh^2 (u)=((th^2 (u))/(1−th^2 (u))) ⇒sh^2 (th^− (u))=(u^2 /(1−u^2 )) sh(th^− (u))=(u/(√(1−u^2 ))) tan^− ((u/(√(1−u^2 ))))=?sin^− (u),u∈[−1,1],t→sint bijection [−(π/2),(π/2)]→[−1,1] u=sin(α)⇒(u/(√(1−u^2 )))=tan(α) tan^− (tan(α))=α sin^− (sinα)=α,since α is unique since we have bijection ⇒injection ⇒tan^− ((u/(√(1−u^2 ))))=sin^− (u) end of proof

$$\mathrm{Hello}\:\mathrm{happy}\:\mathrm{too}\:\mathrm{back}\:\mathrm{withe}\:\mathrm{you}\: \\ $$$$\mathrm{Since} \\ $$$$\left.\mathrm{th}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{bijection}\:\right]−\infty,+\infty\left[−\left\{\mathrm{0}\right\}\rightarrow\right]−\mathrm{1},\mathrm{1}\left[\right. \\ $$$$\left.\Rightarrow\forall\mathrm{u}\in\right]−\mathrm{1},+\mathrm{1}\left[,\exists!\mathrm{x}\in\mathbb{R}^{\ast} \:\:\mid\mathrm{u}=\mathrm{th}\left(\mathrm{x}\right)\right. \\ $$$$\mathrm{sin}^{−} \left(\mathrm{th}\left(\mathrm{x}\right)\right)=\mathrm{sin}^{−} \left(\mathrm{u}\right) \\ $$$$\mathrm{tan}^{−} \left(\mathrm{sh}\left(\mathrm{x}\right)\right)=\mathrm{tan}^{−} \left(\mathrm{sh}\left(\mathrm{th}^{−} \left(\mathrm{u}\right)\right)\right) \\ $$$$\mathrm{th}\left(\mathrm{u}\right)=\frac{\mathrm{sh}\left(\mathrm{u}\right)}{\mathrm{ch}\left(\mathrm{u}\right)} \\ $$$$\mathrm{ch}^{\mathrm{2}} −\mathrm{sh}^{\mathrm{2}} =\mathrm{1}\Rightarrow \\ $$$$\mathrm{sh}^{\mathrm{2}} \left(\mathrm{u}\right)=\frac{\mathrm{th}^{\mathrm{2}} \left(\mathrm{u}\right)}{\mathrm{1}−\mathrm{th}^{\mathrm{2}} \left(\mathrm{u}\right)} \\ $$$$\Rightarrow\mathrm{sh}^{\mathrm{2}} \left(\mathrm{th}^{−} \left(\mathrm{u}\right)\right)=\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{1}−\mathrm{u}^{\mathrm{2}} } \\ $$$$\mathrm{sh}\left(\mathrm{th}^{−} \left(\mathrm{u}\right)\right)=\frac{\mathrm{u}}{\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }} \\ $$$$\mathrm{tan}^{−} \left(\frac{\mathrm{u}}{\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}\right)=?\mathrm{sin}^{−} \left(\mathrm{u}\right),\mathrm{u}\in\left[−\mathrm{1},\mathrm{1}\right],\mathrm{t}\rightarrow\mathrm{sint}\:\mathrm{bijection}\:\left[−\frac{\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right]\rightarrow\left[−\mathrm{1},\mathrm{1}\right] \\ $$$$ \\ $$$$\mathrm{u}=\mathrm{sin}\left(\alpha\right)\Rightarrow\frac{\mathrm{u}}{\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}=\mathrm{tan}\left(\alpha\right) \\ $$$$\mathrm{tan}^{−} \left(\mathrm{tan}\left(\alpha\right)\right)=\alpha \\ $$$$\mathrm{sin}^{−} \left(\mathrm{sin}\alpha\right)=\alpha,\mathrm{since}\:\alpha\:\mathrm{is}\:\mathrm{unique}\:\mathrm{since}\:\mathrm{we}\:\mathrm{have}\:\mathrm{bijection}\:\Rightarrow\mathrm{injection} \\ $$$$\Rightarrow\mathrm{tan}^{−} \left(\frac{\mathrm{u}}{\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}\right)=\mathrm{sin}^{−} \left(\mathrm{u}\right) \\ $$$$\mathrm{end}\:\mathrm{of}\:\mathrm{proof} \\ $$

Commented by Tony Lin last updated on 31/Dec/19

thanks sir

$${thanks}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com