
Question Number 77474 by 21042004 last updated on 06/Jan/20
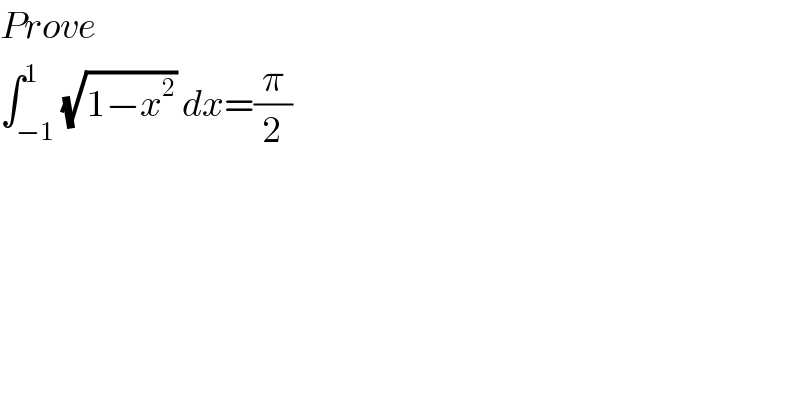
$${Prove} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}=\frac{\pi}{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 06/Jan/20
![let I =∫_(−1) ^1 (√(1−x^2 ))dx ⇒ I =2∫_0 ^1 (√(1−x^2 ))dx changement x=sinθ give I =2∫_0 ^(π/2) cosθ cosθ dθ =∫_0 ^(π/2) (1+cos(2θ)dθ =(π/2) +[(1/2)sin(2θ)]_0 ^(π/2) =(π/2)+0 =(π/2).](Q77498.png)
$${let}\:{I}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx}\:\Rightarrow\:{I}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx}\:{changement}\:{x}={sin}\theta \\ $$$${give}\:{I}\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\theta\:{cos}\theta\:{d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right){d}\theta\right. \\ $$$$=\frac{\pi}{\mathrm{2}}\:+\left[\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\pi}{\mathrm{2}}+\mathrm{0}\:=\frac{\pi}{\mathrm{2}}. \\ $$
Answered by MJS last updated on 06/Jan/20
![(1) y=(√(1−x^2 )) is the upper half of the circle with center ((0),(0) ) and radius r=1 ⇒ the integral is half of the circle area =(1/2)r^2 π=(π/2) (2) ∫(√(1−x^2 ))dx= [t=arcsin x → dx=(√(1−x^2 ))dt] =∫cos^2 t dt=(1/2)(t+sin t cos t)= =(1/2)(x(√(1−x^2 ))+arcsin x) +C ⇒ the integral is (π/2)](Q77475.png)
$$\left(\mathrm{1}\right)\:{y}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{the}\:\mathrm{upper}\:\mathrm{half}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle} \\ $$$$\mathrm{with}\:\mathrm{center}\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\mathrm{and}\:\mathrm{radius}\:{r}=\mathrm{1}\:\Rightarrow\:\mathrm{the}\:\mathrm{integral} \\ $$$$\mathrm{is}\:\mathrm{half}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{area}\:=\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} \pi=\frac{\pi}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\int\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{t}=\mathrm{arcsin}\:{x}\:\rightarrow\:{dx}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dt}\right] \\ $$$$\:\:\:\:\:\:\:\:=\int\mathrm{cos}^{\mathrm{2}} \:{t}\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}\left({t}+\mathrm{sin}\:{t}\:\mathrm{cos}\:{t}\right)= \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left({x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+\mathrm{arcsin}\:{x}\right)\:+{C} \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{the}\:\mathrm{integral}\:\mathrm{is}\:\frac{\pi}{\mathrm{2}} \\ $$
