
Question Number 77988 by ajfour last updated on 12/Jan/20

Commented by ajfour last updated on 12/Jan/20
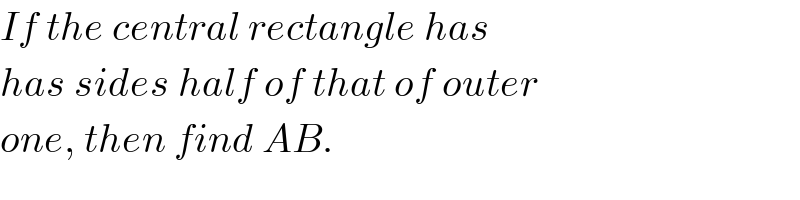
$${If}\:{the}\:{central}\:{rectangle}\:{has} \\ $$$${has}\:{sides}\:{half}\:{of}\:{that}\:{of}\:{outer} \\ $$$${one},\:{then}\:{find}\:{AB}. \\ $$
Answered by mr W last updated on 12/Jan/20
![C(0,c) A(a,0) B(b,0) Eqn. of CA: ((y−1)/(c−1))=((x−(d/2))/(0−(d/2))) point A: ((0−1)/(c−1))=((a−(d/2))/(0−(d/2))) ⇒a=(d/2)(1+(1/(c−1))) Eqn. of CB: ((y−2)/(c−2))=((x−d)/(0−d)) point B: ((0−2)/(c−2))=((b−d)/(0−d)) ⇒b=d(1+(2/(c−2))) AB=b−a=(d/2)(1+(4/(c−2))−(1/(c−1))) AC=(√(a^2 +c^2 )) AC=AB (√(a^2 +c^2 ))=b−a c^2 =b(b−2a) c^2 =d(1+(2/(c−2)))[d(1+(2/(c−2)))−2×(d/2)(1+(1/(c−1)))] c^2 =d^2 (1+(2/(c−2)))((2/(c−2))−(1/(c−1))) c^2 =(d^2 c^2 /((c−2)^2 (c−1))) (c−2)^2 (c−1)−d^2 =0 let t=c−2 ⇒t^3 +t^2 −d^2 =0 let t=s−(1/3) (s−(1/3))^3 +(s−(1/3))^2 −d^2 =0 s^3 −(s/3)+((2/(27))−d^2 )=0 s=(((√(((1/(27))−(d^2 /2))^2 −(1/(729))))−(1/(27))+(d^2 /2)))^(1/3) −(((√(((1/(27))−(d^2 /2))^2 −(1/(729))))+(1/(27))−(d^2 /2)))^(1/3) t=c−2=(((√(((1/(27))−(d^2 /2))^2 −(1/(729))))−(1/(27))+(d^2 /2)))^(1/3) −(((√(((1/(27))−(d^2 /2))^2 −(1/(729))))+(1/(27))−(d^2 /2)))^(1/3) −(1/3) ⇒c=(5/3)+(((√(((1/(27))−(d^2 /2))^2 −(1/(729))))−(1/(27))+(d^2 /2)))^(1/3) −(((√(((1/(27))−(d^2 /2))^2 −(1/(729))))+(1/(27))−(d^2 /2)))^(1/3) −(1/3) AB=(d/2)(1+(4/(c−2))−(1/(c−1)))](Q77992.png)
$${C}\left(\mathrm{0},{c}\right) \\ $$$${A}\left({a},\mathrm{0}\right) \\ $$$${B}\left({b},\mathrm{0}\right) \\ $$$${Eqn}.\:{of}\:{CA}: \\ $$$$\frac{{y}−\mathrm{1}}{{c}−\mathrm{1}}=\frac{{x}−\frac{{d}}{\mathrm{2}}}{\mathrm{0}−\frac{{d}}{\mathrm{2}}} \\ $$$${point}\:{A}: \\ $$$$\frac{\mathrm{0}−\mathrm{1}}{{c}−\mathrm{1}}=\frac{{a}−\frac{{d}}{\mathrm{2}}}{\mathrm{0}−\frac{{d}}{\mathrm{2}}} \\ $$$$\Rightarrow{a}=\frac{{d}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{{c}−\mathrm{1}}\right) \\ $$$$ \\ $$$${Eqn}.\:{of}\:{CB}: \\ $$$$\frac{{y}−\mathrm{2}}{{c}−\mathrm{2}}=\frac{{x}−{d}}{\mathrm{0}−{d}} \\ $$$${point}\:{B}: \\ $$$$\frac{\mathrm{0}−\mathrm{2}}{{c}−\mathrm{2}}=\frac{{b}−{d}}{\mathrm{0}−{d}} \\ $$$$\Rightarrow{b}={d}\left(\mathrm{1}+\frac{\mathrm{2}}{{c}−\mathrm{2}}\right) \\ $$$${AB}={b}−{a}=\frac{{d}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{4}}{{c}−\mathrm{2}}−\frac{\mathrm{1}}{{c}−\mathrm{1}}\right) \\ $$$${AC}=\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$${AC}={AB} \\ $$$$\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }={b}−{a} \\ $$$${c}^{\mathrm{2}} ={b}\left({b}−\mathrm{2}{a}\right) \\ $$$${c}^{\mathrm{2}} ={d}\left(\mathrm{1}+\frac{\mathrm{2}}{{c}−\mathrm{2}}\right)\left[{d}\left(\mathrm{1}+\frac{\mathrm{2}}{{c}−\mathrm{2}}\right)−\mathrm{2}×\frac{{d}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{{c}−\mathrm{1}}\right)\right] \\ $$$${c}^{\mathrm{2}} ={d}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{2}}{{c}−\mathrm{2}}\right)\left(\frac{\mathrm{2}}{{c}−\mathrm{2}}−\frac{\mathrm{1}}{{c}−\mathrm{1}}\right) \\ $$$${c}^{\mathrm{2}} =\frac{{d}^{\mathrm{2}} {c}^{\mathrm{2}} }{\left({c}−\mathrm{2}\right)^{\mathrm{2}} \left({c}−\mathrm{1}\right)} \\ $$$$\left({c}−\mathrm{2}\right)^{\mathrm{2}} \left({c}−\mathrm{1}\right)−{d}^{\mathrm{2}} =\mathrm{0} \\ $$$${let}\:{t}={c}−\mathrm{2} \\ $$$$\Rightarrow{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −{d}^{\mathrm{2}} =\mathrm{0} \\ $$$${let}\:{t}={s}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left({s}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} +\left({s}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} −{d}^{\mathrm{2}} =\mathrm{0} \\ $$$${s}^{\mathrm{3}} −\frac{{s}}{\mathrm{3}}+\left(\frac{\mathrm{2}}{\mathrm{27}}−{d}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${s}=\sqrt[{\mathrm{3}}]{\sqrt{\left(\frac{\mathrm{1}}{\mathrm{27}}−\frac{{d}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{729}}}−\frac{\mathrm{1}}{\mathrm{27}}+\frac{{d}^{\mathrm{2}} }{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\left(\frac{\mathrm{1}}{\mathrm{27}}−\frac{{d}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{729}}}+\frac{\mathrm{1}}{\mathrm{27}}−\frac{{d}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$${t}={c}−\mathrm{2}=\sqrt[{\mathrm{3}}]{\sqrt{\left(\frac{\mathrm{1}}{\mathrm{27}}−\frac{{d}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{729}}}−\frac{\mathrm{1}}{\mathrm{27}}+\frac{{d}^{\mathrm{2}} }{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\left(\frac{\mathrm{1}}{\mathrm{27}}−\frac{{d}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{729}}}+\frac{\mathrm{1}}{\mathrm{27}}−\frac{{d}^{\mathrm{2}} }{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{c}=\frac{\mathrm{5}}{\mathrm{3}}+\sqrt[{\mathrm{3}}]{\sqrt{\left(\frac{\mathrm{1}}{\mathrm{27}}−\frac{{d}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{729}}}−\frac{\mathrm{1}}{\mathrm{27}}+\frac{{d}^{\mathrm{2}} }{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\left(\frac{\mathrm{1}}{\mathrm{27}}−\frac{{d}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{729}}}+\frac{\mathrm{1}}{\mathrm{27}}−\frac{{d}^{\mathrm{2}} }{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${AB}=\frac{{d}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{4}}{{c}−\mathrm{2}}−\frac{\mathrm{1}}{{c}−\mathrm{1}}\right) \\ $$
Commented by ajfour last updated on 13/Jan/20
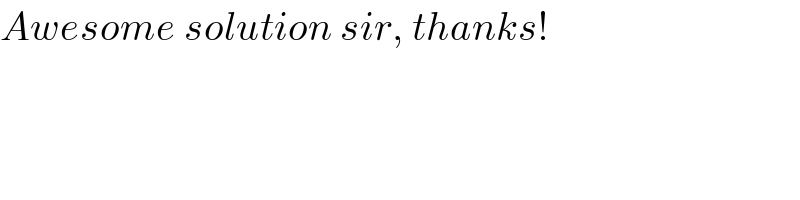
$${Awesome}\:{solution}\:{sir},\:{thanks}! \\ $$
Commented by ajfour last updated on 13/Jan/20

$${its}\:{alright}\:{sir},\:{i}\:{shall}\:{consult} \\ $$$${you}\:{again}.. \\ $$
Commented by mr W last updated on 13/Jan/20

$${sir},\:{please}\:{recheck}: \\ $$$$\left({c}−\mathrm{2}\right)^{\mathrm{2}} \left({c}−\mathrm{1}\right)={d}^{\mathrm{2}} \:{is}\:{correct}.\:{with}\:{t}={c}−\mathrm{2} \\ $$$${we}\:{get}\:{t}^{\mathrm{3}} +{t}={d}^{\mathrm{2}} .\:{not}\:{t}^{\mathrm{3}} −{t}=\mathrm{2}{d}! \\ $$
Commented by MJS last updated on 13/Jan/20

$$\mathrm{to}\:\mathrm{mrW}:\:\mathrm{our}\:\mathrm{friend}'\mathrm{s}\:\mathrm{new}\:\mathrm{ID}\:\mathrm{is}\:\mathrm{Pratah} \\ $$
Commented by mr W last updated on 13/Jan/20

$${yes}.\:{i}\:{knew}\:{this}\:{as}\:{soon}\:{the}\:{first} \\ $$$${question}\:{with}\:{the}\:{new}\:{id}\:{was}\:{posted}. \\ $$
