
Question Number 78693 by TawaTawa last updated on 19/Jan/20
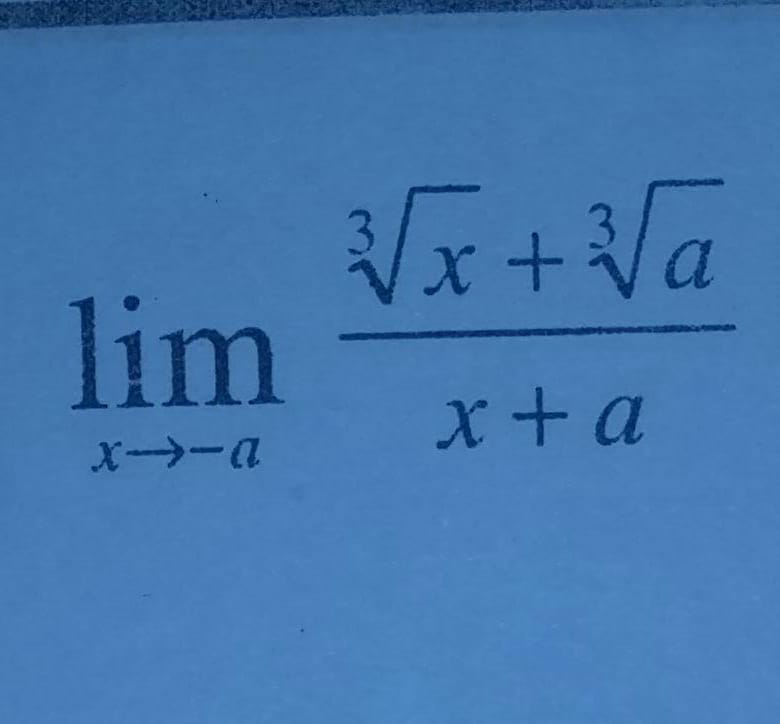
Commented by abdomathmax last updated on 20/Jan/20
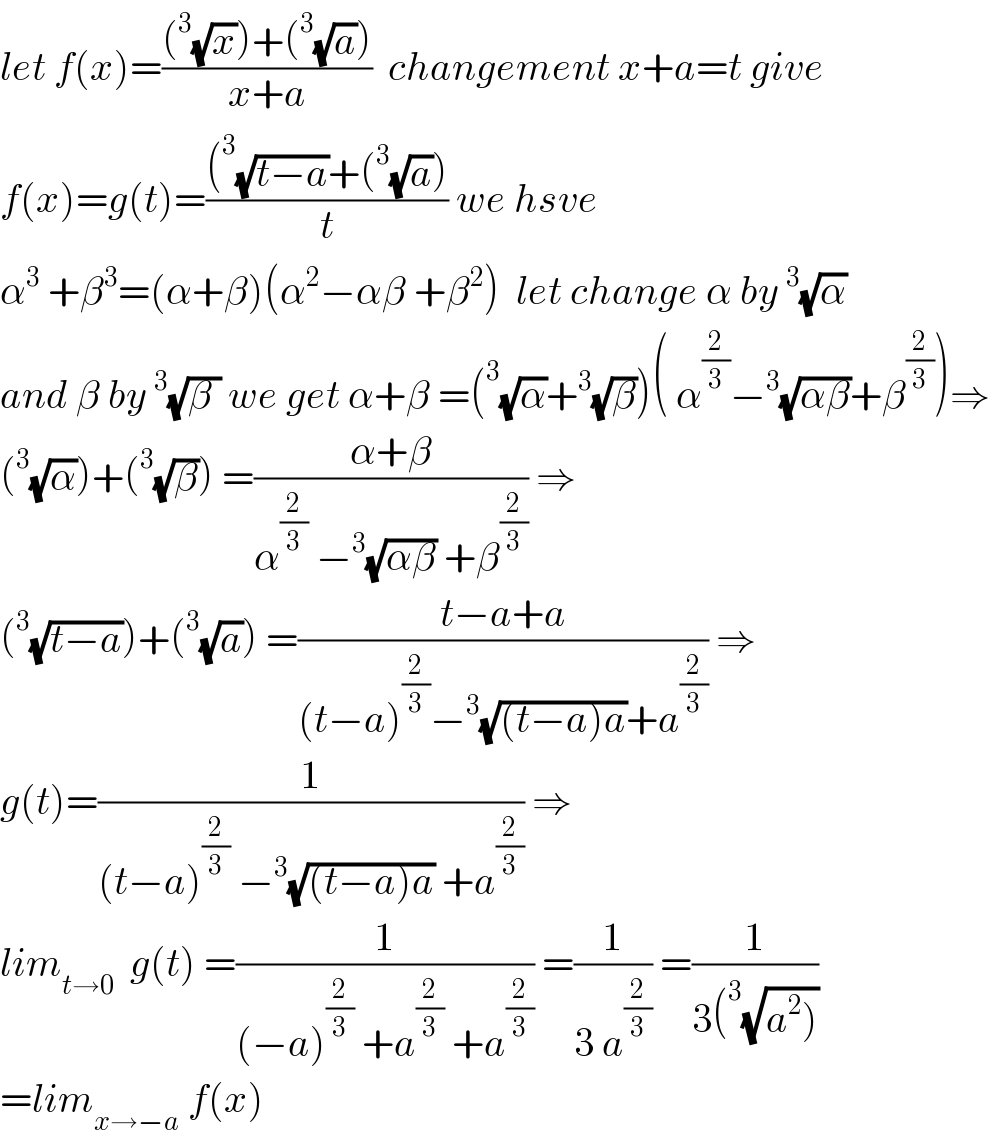
$${let}\:{f}\left({x}\right)=\frac{\left(^{\mathrm{3}} \sqrt{{x}}\right)+\left(^{\mathrm{3}} \sqrt{{a}}\right)}{{x}+{a}}\:\:{changement}\:{x}+{a}={t}\:{give} \\ $$$${f}\left({x}\right)={g}\left({t}\right)=\frac{\left(^{\mathrm{3}} \sqrt{{t}−{a}}+\left(^{\mathrm{3}} \sqrt{{a}}\right)\right.}{{t}}\:{we}\:{hsve} \\ $$$$\alpha^{\mathrm{3}} \:+\beta^{\mathrm{3}} =\left(\alpha+\beta\right)\left(\alpha^{\mathrm{2}} −\alpha\beta\:+\beta^{\mathrm{2}} \right)\:\:{let}\:{change}\:\alpha\:{by}\:^{\mathrm{3}} \sqrt{\alpha} \\ $$$${and}\:\beta\:{by}\:^{\mathrm{3}} \sqrt{\beta\:}\:{we}\:{get}\:\alpha+\beta\:=\left(^{\mathrm{3}} \sqrt{\alpha}+^{\mathrm{3}} \sqrt{\beta}\right)\left(\:\alpha^{\frac{\mathrm{2}}{\mathrm{3}}} −^{\mathrm{3}} \sqrt{\alpha\beta}+\beta^{\frac{\mathrm{2}}{\mathrm{3}}} \right)\Rightarrow \\ $$$$\left(^{\mathrm{3}} \sqrt{\alpha}\right)+\left(^{\mathrm{3}} \sqrt{\beta}\right)\:=\frac{\alpha+\beta}{\alpha^{\frac{\mathrm{2}}{\mathrm{3}}} \:−^{\mathrm{3}} \sqrt{\alpha\beta}\:+\beta^{\frac{\mathrm{2}}{\mathrm{3}}} }\:\Rightarrow \\ $$$$\left(^{\mathrm{3}} \sqrt{{t}−{a}}\right)+\left(^{\mathrm{3}} \sqrt{{a}}\right)\:=\frac{{t}−{a}+{a}}{\left({t}−{a}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} −^{\mathrm{3}} \sqrt{\left({t}−{a}\right){a}}+{a}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:\Rightarrow \\ $$$${g}\left({t}\right)=\frac{\mathrm{1}}{\left({t}−{a}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:−^{\mathrm{3}} \sqrt{\left({t}−{a}\right){a}}\:+{a}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:\Rightarrow \\ $$$${lim}_{{t}\rightarrow\mathrm{0}} \:\:{g}\left({t}\right)\:=\frac{\mathrm{1}}{\left(−{a}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:+{a}^{\frac{\mathrm{2}}{\mathrm{3}}} \:+{a}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:=\frac{\mathrm{1}}{\mathrm{3}\:{a}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:=\frac{\mathrm{1}}{\mathrm{3}\left(^{\mathrm{3}} \sqrt{\left.{a}^{\mathrm{2}} \right)}\right.} \\ $$$$={lim}_{{x}\rightarrow−{a}} \:{f}\left({x}\right) \\ $$
Commented by TawaTawa last updated on 20/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 20/Jan/20

$${you}\:{are}\:{welcome} \\ $$
Answered by john santu last updated on 20/Jan/20
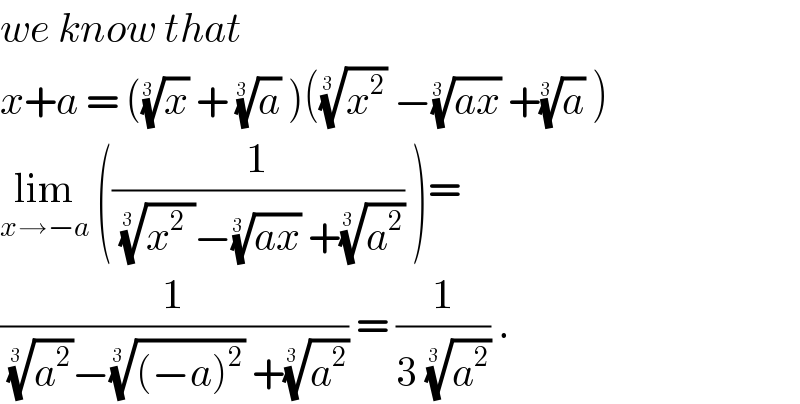
$${we}\:{know}\:{that}\: \\ $$$${x}+{a}\:=\:\left(\sqrt[{\mathrm{3}\:}]{{x}}\:+\:\sqrt[{\mathrm{3}\:}]{{a}}\:\right)\left(\sqrt[{\mathrm{3}\:}]{{x}^{\mathrm{2}} }\:−\sqrt[{\mathrm{3}\:}]{{ax}}\:+\sqrt[{\mathrm{3}\:}]{{a}}\:\right)\: \\ $$$$\underset{{x}\rightarrow−{a}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\sqrt[{\mathrm{3}\:}]{{x}^{\mathrm{2}} \:}−\sqrt[{\mathrm{3}\:}]{{ax}}\:+\sqrt[{\mathrm{3}\:}]{{a}^{\mathrm{2}} }}\:\right)=\: \\ $$$$\frac{\mathrm{1}}{\sqrt[{\mathrm{3}\:}]{{a}^{\mathrm{2}} }−\sqrt[{\mathrm{3}\:}]{\left(−{a}\right)^{\mathrm{2}} }\:+\sqrt[{\mathrm{3}\:}]{{a}^{\mathrm{2}} }}\:=\:\frac{\mathrm{1}}{\mathrm{3}\:\sqrt[{\mathrm{3}\:}]{{a}^{\mathrm{2}} }}\:. \\ $$
Commented by TawaTawa last updated on 20/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
