Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 78800 by Tony Lin last updated on 20/Jan/20

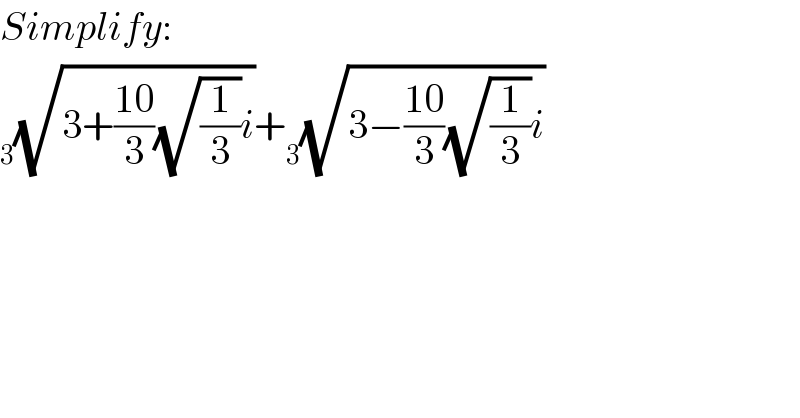
Simplify: _3 (√(3+((10)/3)(√(1/3))i))+ _3 (√(3−((10)/3)(√(1/3))i))

$${Simplify}: \\ $$$$\underset{\mathrm{3}} {\:}\sqrt{\mathrm{3}+\frac{\mathrm{10}}{\mathrm{3}}\sqrt{\frac{\mathrm{1}}{\mathrm{3}}}{i}}+\underset{\mathrm{3}} {\:}\sqrt{\mathrm{3}−\frac{\mathrm{10}}{\mathrm{3}}\sqrt{\frac{\mathrm{1}}{\mathrm{3}}}{i}} \\ $$

Commented by mathmax by abdo last updated on 20/Jan/20

A =(3+((10)/(3(√3)))i)^(1/3) +(3−((10)/(3(√3)))i)^(1/3) we have ∣3+((10)/(3(√3)))i∣ =(√(3^2 +((10^2 )/(27)) ))=(√((37×9 +100)/(27)))=(√(((433)/(37))=r_0 )) ⇒3+((10)/(3(√3)))i =r_0 e^(iarctan(((10)/(9(√3))))) ⇒(3+((10)/(3(√3)))i)^(1/3) =(r_0 )^(1/3) e^((i/3)arctan(((10)/(9(√3))))) also (3−((10)/(3(√3)))i)^(1/3) =(r_0 )^(1/3) e^(−(i/3)arctan(((10)/(9(√3))))) ⇒ A =(r_0 )^(1/3) (2cos((1/3)arctan(((10)/(9(√3)))))=2(r_0 )^(1/3) cos((1/3)arctan(((10)/(9(√3)))))

$${A}\:=\left(\mathrm{3}+\frac{\mathrm{10}}{\mathrm{3}\sqrt{\mathrm{3}}}{i}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:+\left(\mathrm{3}−\frac{\mathrm{10}}{\mathrm{3}\sqrt{\mathrm{3}}}{i}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${we}\:{have}\:\mid\mathrm{3}+\frac{\mathrm{10}}{\mathrm{3}\sqrt{\mathrm{3}}}{i}\mid\:=\sqrt{\mathrm{3}^{\mathrm{2}} \:+\frac{\mathrm{10}^{\mathrm{2}} }{\mathrm{27}}\:}=\sqrt{\frac{\mathrm{37}×\mathrm{9}\:+\mathrm{100}}{\mathrm{27}}}=\sqrt{\frac{\mathrm{433}}{\mathrm{37}}={r}_{\mathrm{0}} } \\ $$$$\Rightarrow\mathrm{3}+\frac{\mathrm{10}}{\mathrm{3}\sqrt{\mathrm{3}}}{i}\:={r}_{\mathrm{0}} \:{e}^{{iarctan}\left(\frac{\mathrm{10}}{\mathrm{9}\sqrt{\mathrm{3}}}\right)} \:\Rightarrow\left(\mathrm{3}+\frac{\mathrm{10}}{\mathrm{3}\sqrt{\mathrm{3}}}{i}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\left({r}_{\mathrm{0}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:{e}^{\frac{{i}}{\mathrm{3}}{arctan}\left(\frac{\mathrm{10}}{\mathrm{9}\sqrt{\mathrm{3}}}\right)} \\ $$$${also}\:\left(\mathrm{3}−\frac{\mathrm{10}}{\mathrm{3}\sqrt{\mathrm{3}}}{i}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:=\left({r}_{\mathrm{0}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:{e}^{−\frac{{i}}{\mathrm{3}}{arctan}\left(\frac{\mathrm{10}}{\mathrm{9}\sqrt{\mathrm{3}}}\right)} \:\Rightarrow \\ $$$${A}\:=\left({r}_{\mathrm{0}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\left(\mathrm{2}{cos}\left(\frac{\mathrm{1}}{\mathrm{3}}{arctan}\left(\frac{\mathrm{10}}{\mathrm{9}\sqrt{\mathrm{3}}}\right)\right)=\mathrm{2}\left({r}_{\mathrm{0}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:{cos}\left(\frac{\mathrm{1}}{\mathrm{3}}{arctan}\left(\frac{\mathrm{10}}{\mathrm{9}\sqrt{\mathrm{3}}}\right)\right)\right. \\ $$

Commented by Tony Lin last updated on 21/Jan/20

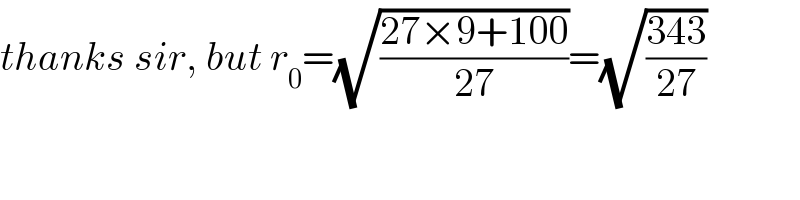
thanks sir, but r_0 =(√((27×9+100)/(27)))=(√((343)/(27)))

$${thanks}\:{sir},\:{but}\:{r}_{\mathrm{0}} =\sqrt{\frac{\mathrm{27}×\mathrm{9}+\mathrm{100}}{\mathrm{27}}}=\sqrt{\frac{\mathrm{343}}{\mathrm{27}}} \\ $$

Commented by mathmax by abdo last updated on 21/Jan/20

yes

$${yes} \\ $$

Answered by MJS last updated on 20/Jan/20

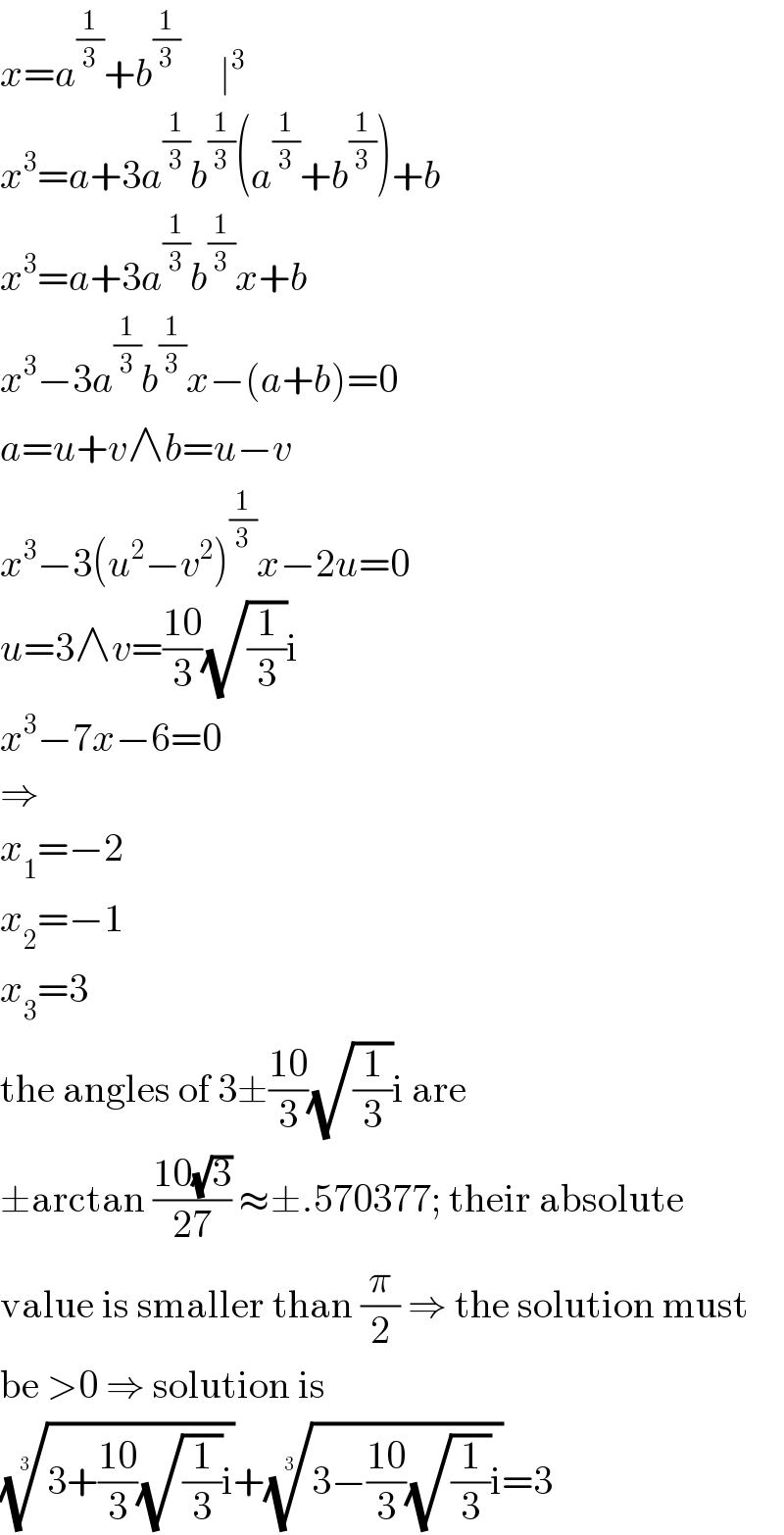
x=a^(1/3) +b^(1/3) ∣^3 x^3 =a+3a^(1/3) b^(1/3) (a^(1/3) +b^(1/3) )+b x^3 =a+3a^(1/3) b^(1/3) x+b x^3 −3a^(1/3) b^(1/3) x−(a+b)=0 a=u+v∧b=u−v x^3 −3(u^2 −v^2 )^(1/3) x−2u=0 u=3∧v=((10)/3)(√(1/3))i x^3 −7x−6=0 ⇒ x_1 =−2 x_2 =−1 x_3 =3 the angles of 3±((10)/3)(√(1/3))i are ±arctan ((10(√3))/(27)) ≈±.570377; their absolute value is smaller than (π/2) ⇒ the solution must be >0 ⇒ solution is ((3+((10)/3)(√(1/3))i))^(1/3) +((3−((10)/3)(√(1/3))i))^(1/3) =3

$${x}={a}^{\frac{\mathrm{1}}{\mathrm{3}}} +{b}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\:\:\:\:\mid^{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} ={a}+\mathrm{3}{a}^{\frac{\mathrm{1}}{\mathrm{3}}} {b}^{\frac{\mathrm{1}}{\mathrm{3}}} \left({a}^{\frac{\mathrm{1}}{\mathrm{3}}} +{b}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)+{b} \\ $$$${x}^{\mathrm{3}} ={a}+\mathrm{3}{a}^{\frac{\mathrm{1}}{\mathrm{3}}} {b}^{\frac{\mathrm{1}}{\mathrm{3}}} {x}+{b} \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{a}^{\frac{\mathrm{1}}{\mathrm{3}}} {b}^{\frac{\mathrm{1}}{\mathrm{3}}} {x}−\left({a}+{b}\right)=\mathrm{0} \\ $$$${a}={u}+{v}\wedge{b}={u}−{v} \\ $$$${x}^{\mathrm{3}} −\mathrm{3}\left({u}^{\mathrm{2}} −{v}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} {x}−\mathrm{2}{u}=\mathrm{0} \\ $$$${u}=\mathrm{3}\wedge{v}=\frac{\mathrm{10}}{\mathrm{3}}\sqrt{\frac{\mathrm{1}}{\mathrm{3}}}\mathrm{i} \\ $$$${x}^{\mathrm{3}} −\mathrm{7}{x}−\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1}} =−\mathrm{2} \\ $$$${x}_{\mathrm{2}} =−\mathrm{1} \\ $$$${x}_{\mathrm{3}} =\mathrm{3} \\ $$$$\mathrm{the}\:\mathrm{angles}\:\mathrm{of}\:\mathrm{3}\pm\frac{\mathrm{10}}{\mathrm{3}}\sqrt{\frac{\mathrm{1}}{\mathrm{3}}}\mathrm{i}\:\mathrm{are} \\ $$$$\pm\mathrm{arctan}\:\frac{\mathrm{10}\sqrt{\mathrm{3}}}{\mathrm{27}}\:\approx\pm.\mathrm{570377};\:\mathrm{their}\:\mathrm{absolute} \\ $$$$\mathrm{value}\:\mathrm{is}\:\mathrm{smaller}\:\mathrm{than}\:\frac{\pi}{\mathrm{2}}\:\Rightarrow\:\mathrm{the}\:\mathrm{solution}\:\mathrm{must} \\ $$$$\mathrm{be}\:>\mathrm{0}\:\Rightarrow\:\mathrm{solution}\:\mathrm{is} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{3}+\frac{\mathrm{10}}{\mathrm{3}}\sqrt{\frac{\mathrm{1}}{\mathrm{3}}}\mathrm{i}}+\sqrt[{\mathrm{3}}]{\mathrm{3}−\frac{\mathrm{10}}{\mathrm{3}}\sqrt{\frac{\mathrm{1}}{\mathrm{3}}}\mathrm{i}}=\mathrm{3} \\ $$

Commented by Tony Lin last updated on 21/Jan/20

thanks sir, but if we originally use Cardano′s method to solve x^3 +px+q=0 how can we simplify the answer to become more beautiful without using factorization or what we can do is only cube it and solve it in a complicated and slow way

$${thanks}\:{sir},\:{but}\:{if}\:{we}\:{originally}\:{use}\: \\ $$$${Cardano}'{s}\:{method}\:{to}\:{solve}\: \\ $$$${x}^{\mathrm{3}} +{px}+{q}=\mathrm{0} \\ $$$${how}\:{can}\:{we}\:{simplify}\:{the}\:{answer}\:{to} \\ $$$${become}\:{more}\:{beautiful}\:{without}\:{using} \\ $$$${factorization} \\ $$$${or}\:{what}\:{we}\:{can}\:{do}\:{is}\:{only}\:{cube}\:{it} \\ $$$${and}\:{solve}\:{it}\:{in}\:{a}\:{complicated}\:{and} \\ $$$${slow}\:{way} \\ $$

Commented by MJS last updated on 21/Jan/20

Cardano doesn′t work when the equation has 3 real roots. x^3 +px+q=0 first, always check all factors of ±q (x−α)(x−β)(x−γ)=x^3 +...−αβγ ⇒ q=−αβγ if we have solutions ∈Z or ∈Q we can simply find them second, calculate D=(p^3 /(27))+(q^2 /4) D≥0 ⇒ Cardano D<0 ⇒ trigonometric solution x_(k+1) =(2/3)(√(−3p))sin ((1/3)(2kπ+arcsin ((9q)/(2(√(−3p^3 )))))) with k=0, 1, 2 the problem with both methods is that the solutions “hide” easier ones like x=(√3)+(√2) but there′s no other way

$$\mathrm{Cardano}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{work}\:\mathrm{when}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{has} \\ $$$$\mathrm{3}\:\mathrm{real}\:\mathrm{roots}. \\ $$$${x}^{\mathrm{3}} +{px}+{q}=\mathrm{0} \\ $$$$\mathrm{first},\:\mathrm{always}\:\mathrm{check}\:\mathrm{all}\:\mathrm{factors}\:\mathrm{of}\:\pm{q} \\ $$$$\left({x}−\alpha\right)\left({x}−\beta\right)\left({x}−\gamma\right)={x}^{\mathrm{3}} +...−\alpha\beta\gamma \\ $$$$\Rightarrow\:{q}=−\alpha\beta\gamma \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{have}\:\mathrm{solutions}\:\in\mathbb{Z}\:\mathrm{or}\:\in\mathbb{Q}\:\mathrm{we}\:\mathrm{can}\:\mathrm{simply} \\ $$$$\mathrm{find}\:\mathrm{them} \\ $$$$\mathrm{second},\:\mathrm{calculate}\:{D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${D}\geqslant\mathrm{0}\:\Rightarrow\:\mathrm{Cardano} \\ $$$${D}<\mathrm{0}\:\Rightarrow\:\mathrm{trigonometric}\:\mathrm{solution} \\ $$$${x}_{{k}+\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}}\sqrt{−\mathrm{3}{p}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}{k}\pi+\mathrm{arcsin}\:\frac{\mathrm{9}{q}}{\mathrm{2}\sqrt{−\mathrm{3}{p}^{\mathrm{3}} }}\right)\right) \\ $$$$\mathrm{with}\:{k}=\mathrm{0},\:\mathrm{1},\:\mathrm{2} \\ $$$$\mathrm{the}\:\mathrm{problem}\:\mathrm{with}\:\mathrm{both}\:\mathrm{methods}\:\mathrm{is}\:\mathrm{that}\:\mathrm{the} \\ $$$$\mathrm{solutions}\:``\mathrm{hide}''\:\mathrm{easier}\:\mathrm{ones}\:\mathrm{like}\:{x}=\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}} \\ $$$$\mathrm{but}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{other}\:\mathrm{way} \\ $$

Commented by MJS last updated on 21/Jan/20

x^3 −7x−6=0 in this case, first try factors of ±6: {−6, −3, −2, −1, 1, 2, 3, 6} and you′re done Cardano doesn′t work because D=(((−7)^3 )/(27))+(((−6)^2 )/4)=−((100)/(27))<0 trigonometric solution gives x_1 =−((√(21))/3)sin ((1/3)arcsin ((9(√(21)))/(49))) x_2 =((2(√(21)))/3)sin ((π/3)+arcsin ((9(√(21)))/(49))) x_3 =−((2(√(21)))/3)cos ((π/6)+arcsin ((9(√(21)))/(49))) and it′s not easy to show x_1 =−1 x_2 =3 x_3 =−2

$${x}^{\mathrm{3}} −\mathrm{7}{x}−\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case},\:\mathrm{first}\:\mathrm{try}\:\mathrm{factors}\:\mathrm{of}\:\pm\mathrm{6}: \\ $$$$\left\{−\mathrm{6},\:−\mathrm{3},\:−\mathrm{2},\:−\mathrm{1},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{6}\right\} \\ $$$$\mathrm{and}\:\mathrm{you}'\mathrm{re}\:\mathrm{done} \\ $$$$\mathrm{Cardano}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{work}\:\mathrm{because} \\ $$$${D}=\frac{\left(−\mathrm{7}\right)^{\mathrm{3}} }{\mathrm{27}}+\frac{\left(−\mathrm{6}\right)^{\mathrm{2}} }{\mathrm{4}}=−\frac{\mathrm{100}}{\mathrm{27}}<\mathrm{0} \\ $$$$\mathrm{trigonometric}\:\mathrm{solution}\:\mathrm{gives} \\ $$$${x}_{\mathrm{1}} =−\frac{\sqrt{\mathrm{21}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{9}\sqrt{\mathrm{21}}}{\mathrm{49}}\right) \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\mathrm{arcsin}\:\frac{\mathrm{9}\sqrt{\mathrm{21}}}{\mathrm{49}}\right) \\ $$$${x}_{\mathrm{3}} =−\frac{\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{3}}\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}+\mathrm{arcsin}\:\frac{\mathrm{9}\sqrt{\mathrm{21}}}{\mathrm{49}}\right) \\ $$$$\mathrm{and}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{show} \\ $$$${x}_{\mathrm{1}} =−\mathrm{1} \\ $$$${x}_{\mathrm{2}} =\mathrm{3} \\ $$$${x}_{\mathrm{3}} =−\mathrm{2} \\ $$

Commented by jagoll last updated on 21/Jan/20

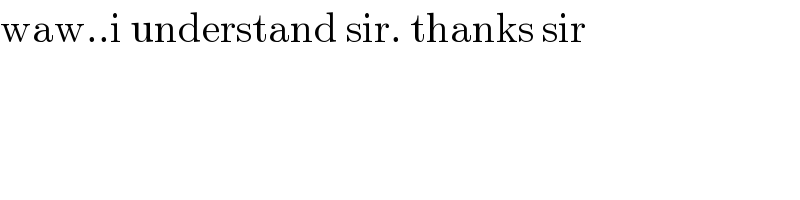
waw..i understand sir. thanks sir

$$\mathrm{waw}..\mathrm{i}\:\mathrm{understand}\:\mathrm{sir}.\:\mathrm{thanks}\:\mathrm{sir} \\ $$

Commented by Tony Lin last updated on 21/Jan/20

thanks sir,and I found that if I use the result from mathmax ((3+((10)/3)(√(1/3))i))^(1/3) +((3−((10)/3)(√(1/3))i))^(1/3) =2(√(7/3))cos[(1/3)arctan(((10)/(9(√3))))] let arctan(((10)/(9(√3))))=θ⇒tanθ=((10)/(9(√3))) ∴cosθ=((9(√3))/(7(√7)))=4cos^3 (θ/3)−3cos(θ/3) let cos(θ/3)=t⇒4t^3 −3t=((9(√3))/(7(√7))) ⇒28(√7)t^3 −21(√7)t−9(√3)=0 ⇒(2(√7)t−3(√3))(14t^2 +3(√(21))t+3)=0 ∴t=(3/2)(√(3/7)) ∴2(√(7/3))cos[(1/3)arctan(((10)/(9(√3))))] =((3+((10)/3)(√(1/3))i))^(1/3) +((3−((10)/3)(√(1/3))i))^(1/3) =3

$${thanks}\:{sir},{and}\:{I}\:{found}\:{that} \\ $$$${if}\:{I}\:{use}\:{the}\:{result}\:{from}\:{mathmax} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{3}+\frac{\mathrm{10}}{\mathrm{3}}\sqrt{\frac{\mathrm{1}}{\mathrm{3}}}{i}}+\sqrt[{\mathrm{3}}]{\mathrm{3}−\frac{\mathrm{10}}{\mathrm{3}}\sqrt{\frac{\mathrm{1}}{\mathrm{3}}}{i}} \\ $$$$=\mathrm{2}\sqrt{\frac{\mathrm{7}}{\mathrm{3}}}{cos}\left[\frac{\mathrm{1}}{\mathrm{3}}{arctan}\left(\frac{\mathrm{10}}{\mathrm{9}\sqrt{\mathrm{3}}}\right)\right] \\ $$$${let}\:{arctan}\left(\frac{\mathrm{10}}{\mathrm{9}\sqrt{\mathrm{3}}}\right)=\theta\Rightarrow{tan}\theta=\frac{\mathrm{10}}{\mathrm{9}\sqrt{\mathrm{3}}} \\ $$$$\therefore{cos}\theta=\frac{\mathrm{9}\sqrt{\mathrm{3}}}{\mathrm{7}\sqrt{\mathrm{7}}}=\mathrm{4}{cos}^{\mathrm{3}} \frac{\theta}{\mathrm{3}}−\mathrm{3}{cos}\frac{\theta}{\mathrm{3}} \\ $$$${let}\:{cos}\frac{\theta}{\mathrm{3}}={t}\Rightarrow\mathrm{4}{t}^{\mathrm{3}} −\mathrm{3}{t}=\frac{\mathrm{9}\sqrt{\mathrm{3}}}{\mathrm{7}\sqrt{\mathrm{7}}} \\ $$$$\Rightarrow\mathrm{28}\sqrt{\mathrm{7}}{t}^{\mathrm{3}} −\mathrm{21}\sqrt{\mathrm{7}}{t}−\mathrm{9}\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}\sqrt{\mathrm{7}}{t}−\mathrm{3}\sqrt{\mathrm{3}}\right)\left(\mathrm{14}{t}^{\mathrm{2}} +\mathrm{3}\sqrt{\mathrm{21}}{t}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\therefore{t}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\frac{\mathrm{3}}{\mathrm{7}}} \\ $$$$\therefore\mathrm{2}\sqrt{\frac{\mathrm{7}}{\mathrm{3}}}{cos}\left[\frac{\mathrm{1}}{\mathrm{3}}{arctan}\left(\frac{\mathrm{10}}{\mathrm{9}\sqrt{\mathrm{3}}}\right)\right] \\ $$$$=\sqrt[{\mathrm{3}}]{\mathrm{3}+\frac{\mathrm{10}}{\mathrm{3}}\sqrt{\frac{\mathrm{1}}{\mathrm{3}}}{i}}+\sqrt[{\mathrm{3}}]{\mathrm{3}−\frac{\mathrm{10}}{\mathrm{3}}\sqrt{\frac{\mathrm{1}}{\mathrm{3}}}{i}} \\ $$$$=\mathrm{3} \\ $$

Commented by msup trace by abdo last updated on 21/Jan/20

thank you for completing the answer

$${thank}\:{you}\:{for}\:{completing}\:{the}\:{answer} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com