
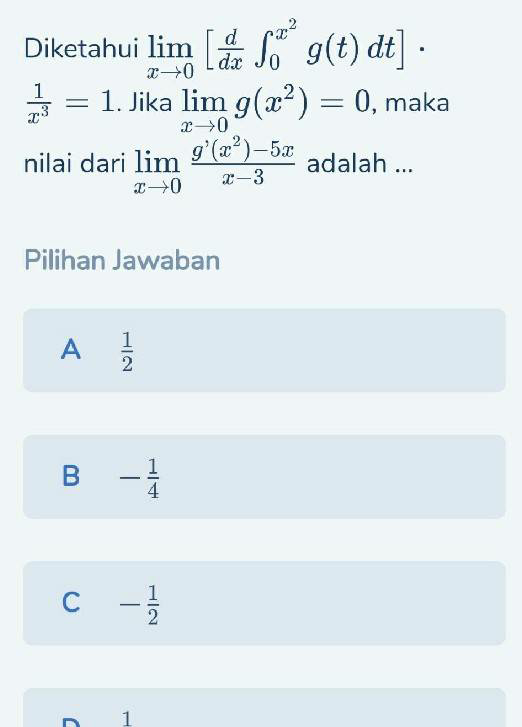
Question Number 78897 by Mikael_786 last updated on 21/Jan/20
Commented by mind is power last updated on 21/Jan/20

$${translate}\:{please} \\ $$
Commented by mr W last updated on 21/Jan/20
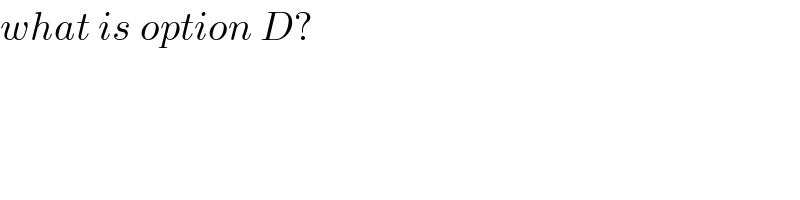
$${what}\:{is}\:{option}\:{D}? \\ $$
Commented by Mikael_786 last updated on 21/Jan/20

$${help}\:{plz} \\ $$
Commented by john santu last updated on 21/Jan/20
![lim_(x→0) [g(x^2 )×2x]×(1/x^3 )=1 lim_(x→0) ((2g(x^2 ))/x^2 )=1 ⇒lim_(x→0) ((2xg′(x^2 ))/(2x))=1 g′(0)=1. now we work lim_(x→0) ((g′(x^2 )−5x)/(x−3))= ((g′(0)−5×0)/(0−3))=−(1/3)](Q78909.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[{g}\left({x}^{\mathrm{2}} \right)×\mathrm{2}{x}\right]×\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}{g}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }=\mathrm{1}\:\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}{xg}'\left({x}^{\mathrm{2}} \right)}{\mathrm{2}{x}}=\mathrm{1} \\ $$$${g}'\left(\mathrm{0}\right)=\mathrm{1}. \\ $$$${now}\:{we}\:{work}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{g}'\left({x}^{\mathrm{2}} \right)−\mathrm{5}{x}}{{x}−\mathrm{3}}= \\ $$$$\frac{{g}'\left(\mathrm{0}\right)−\mathrm{5}×\mathrm{0}}{\mathrm{0}−\mathrm{3}}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by john santu last updated on 21/Jan/20
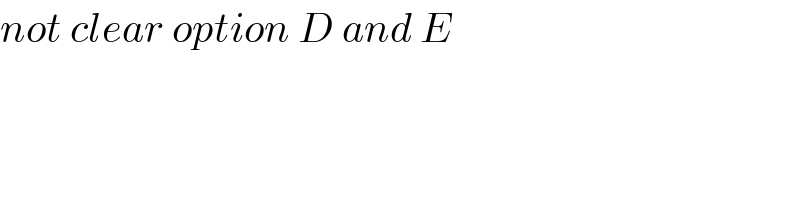
$${not}\:{clear}\:{option}\:{D}\:{and}\:{E} \\ $$
Commented by Mikael_786 last updated on 21/Jan/20

$${thank}\:{you}\:{Sir} \\ $$
Commented by mr W last updated on 21/Jan/20
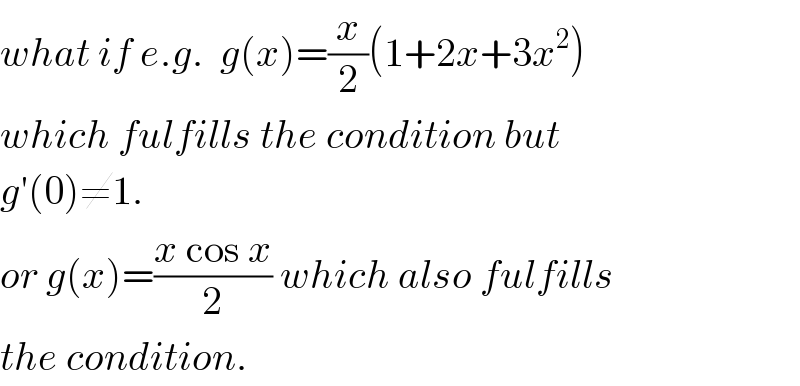
$${what}\:{if}\:{e}.{g}.\:\:{g}\left({x}\right)=\frac{{x}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} \right) \\ $$$${which}\:{fulfills}\:{the}\:{condition}\:{but} \\ $$$${g}'\left(\mathrm{0}\right)\neq\mathrm{1}. \\ $$$${or}\:{g}\left({x}\right)=\frac{{x}\:\mathrm{cos}\:{x}}{\mathrm{2}}\:{which}\:{also}\:{fulfills} \\ $$$${the}\:{condition}. \\ $$
Commented by mr W last updated on 21/Jan/20

$${Mikael}\:{sir}: \\ $$$${please}\:{translate}\:{the}\:{question}\:{and} \\ $$$${tell}\:{the}\:{option}\:{D},\:{or}\:{E}\:{if}\:{exists}! \\ $$
Commented by Mikael_786 last updated on 21/Jan/20
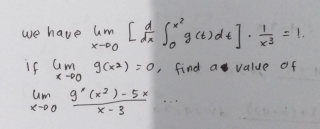
Commented by Mikael_786 last updated on 21/Jan/20
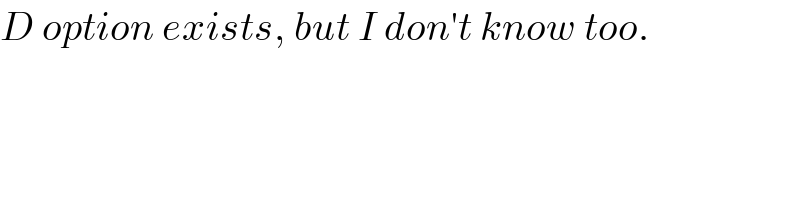
$${D}\:{option}\:{exists},\:{but}\:{I}\:{don}'{t}\:{know}\:{too}. \\ $$
Commented by mr W last updated on 21/Jan/20
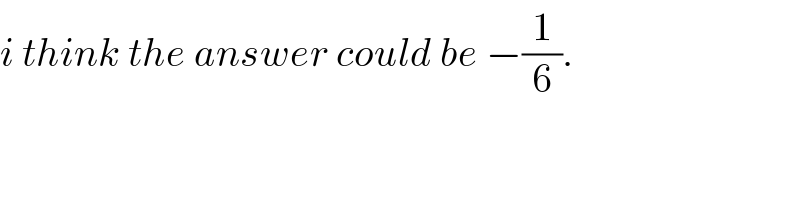
$${i}\:{think}\:{the}\:{answer}\:{could}\:{be}\:−\frac{\mathrm{1}}{\mathrm{6}}. \\ $$
Answered by mr W last updated on 21/Jan/20
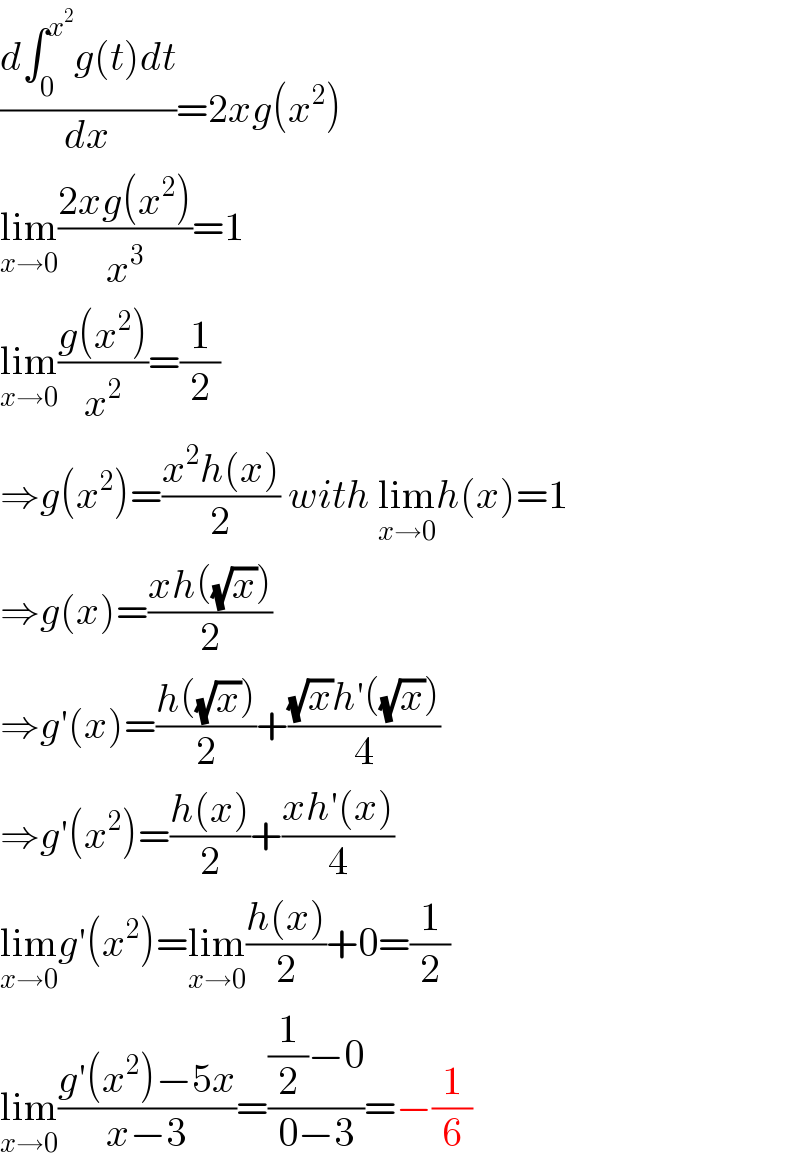
$$\frac{{d}\int_{\mathrm{0}} ^{{x}^{\mathrm{2}} } {g}\left({t}\right){dt}}{{dx}}=\mathrm{2}{xg}\left({x}^{\mathrm{2}} \right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}{xg}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{3}} }=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{g}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{g}\left({x}^{\mathrm{2}} \right)=\frac{{x}^{\mathrm{2}} {h}\left({x}\right)}{\mathrm{2}}\:{with}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{h}\left({x}\right)=\mathrm{1} \\ $$$$\Rightarrow{g}\left({x}\right)=\frac{{xh}\left(\sqrt{{x}}\right)}{\mathrm{2}} \\ $$$$\Rightarrow{g}'\left({x}\right)=\frac{{h}\left(\sqrt{{x}}\right)}{\mathrm{2}}+\frac{\sqrt{{x}}{h}'\left(\sqrt{{x}}\right)}{\mathrm{4}} \\ $$$$\Rightarrow{g}'\left({x}^{\mathrm{2}} \right)=\frac{{h}\left({x}\right)}{\mathrm{2}}+\frac{{xh}'\left({x}\right)}{\mathrm{4}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{g}'\left({x}^{\mathrm{2}} \right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{h}\left({x}\right)}{\mathrm{2}}+\mathrm{0}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{g}'\left({x}^{\mathrm{2}} \right)−\mathrm{5}{x}}{{x}−\mathrm{3}}=\frac{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{0}}{\mathrm{0}−\mathrm{3}}=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Commented by john santu last updated on 21/Jan/20
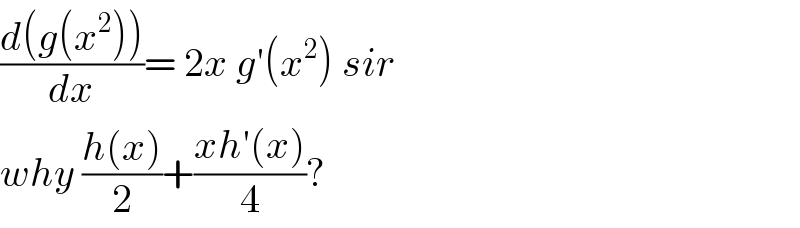
$$\frac{{d}\left({g}\left({x}^{\mathrm{2}} \right)\right)}{{dx}}=\:\mathrm{2}{x}\:{g}'\left({x}^{\mathrm{2}} \right)\:{sir}\: \\ $$$${why}\:\frac{{h}\left({x}\right)}{\mathrm{2}}+\frac{{xh}'\left({x}\right)}{\mathrm{4}}? \\ $$
Commented by mr W last updated on 22/Jan/20

$${by}\:{using}\:{the}\:{form}\:{y}'\:{you}\:{should}\:{be} \\ $$$${very}\:{careful}\:{what}\:{you}\:{really}\:{mean}, \\ $$$${i}.{e}.\:{with}\:{respect}\:{to}\:{what}? \\ $$$${assume}\:{g}\left({x}\right)={x}^{\mathrm{2}} \left(\mathrm{1}+{x}\right).\:{can}\:{you}\:{tell}\:{me} \\ $$$${what}\:{g}'\left({x}^{\mathrm{2}} \right)\:{is}\:{concretely}\:{in}\:{your}\:{eqn}. \\ $$$$\frac{{d}\left({g}\left({x}^{\mathrm{2}} \right)\right)}{{dx}}=\:\mathrm{2}{x}\:{g}'\left({x}^{\mathrm{2}} \right)=? \\ $$
Commented by john santu last updated on 22/Jan/20
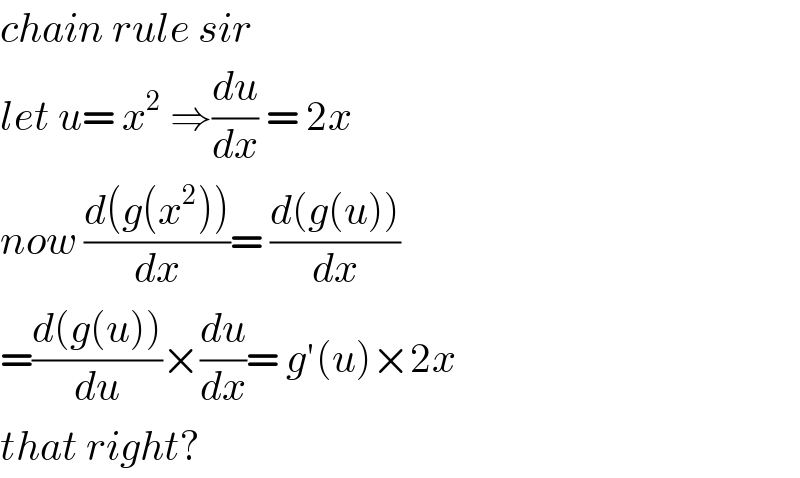
$${chain}\:{rule}\:{sir} \\ $$$${let}\:{u}=\:{x}^{\mathrm{2}} \:\Rightarrow\frac{{du}}{{dx}}\:=\:\mathrm{2}{x} \\ $$$${now}\:\frac{{d}\left({g}\left({x}^{\mathrm{2}} \right)\right)}{{dx}}=\:\frac{{d}\left({g}\left({u}\right)\right)}{{dx}} \\ $$$$=\frac{{d}\left({g}\left({u}\right)\right)}{{du}}×\frac{{du}}{{dx}}=\:{g}'\left({u}\right)×\mathrm{2}{x} \\ $$$${that}\:{right}? \\ $$
Commented by mr W last updated on 22/Jan/20

$${yes}! \\ $$
