
Question Number 79443 by jagoll last updated on 25/Jan/20
![lim_(x→0) [(sin x)^(1/x) +((1/x))^(sin x) ] =](Q79443.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\left(\mathrm{sin}\:\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} +\left(\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{sin}\:\mathrm{x}} \right]\:= \\ $$
Commented by mathmax by abdo last updated on 25/Jan/20
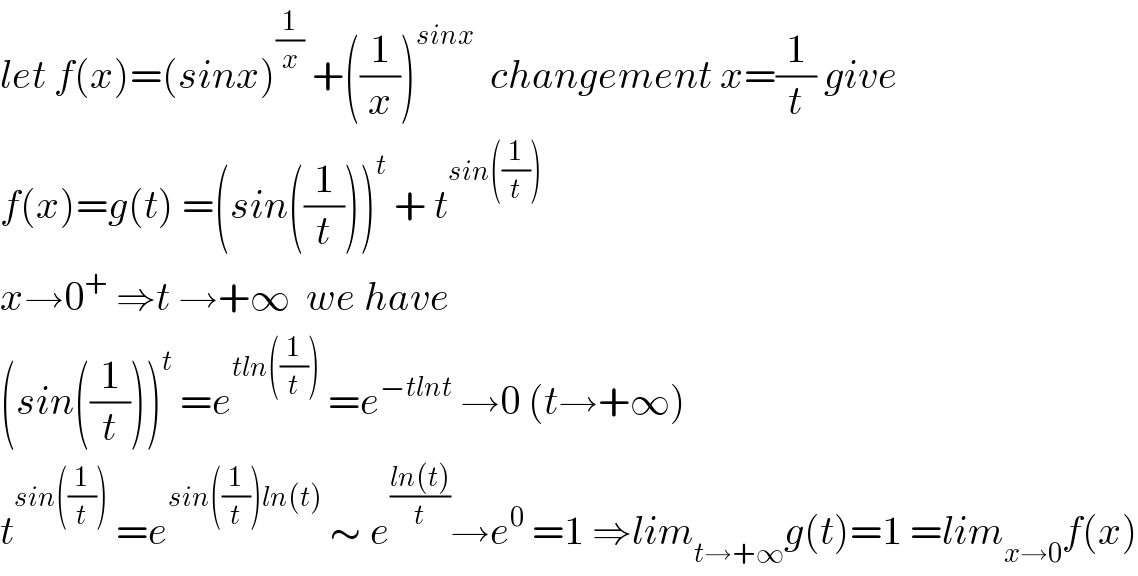
$${let}\:{f}\left({x}\right)=\left({sinx}\right)^{\frac{\mathrm{1}}{{x}}} \:+\left(\frac{\mathrm{1}}{{x}}\right)^{{sinx}} \:\:{changement}\:{x}=\frac{\mathrm{1}}{{t}}\:{give} \\ $$$${f}\left({x}\right)={g}\left({t}\right)\:=\left({sin}\left(\frac{\mathrm{1}}{{t}}\right)\right)^{{t}} \:+\:{t}^{{sin}\left(\frac{\mathrm{1}}{{t}}\right)} \\ $$$${x}\rightarrow\mathrm{0}^{+} \:\Rightarrow{t}\:\rightarrow+\infty\:\:{we}\:{have}\: \\ $$$$\left({sin}\left(\frac{\mathrm{1}}{{t}}\right)\right)^{{t}} \:={e}^{{tln}\left(\frac{\mathrm{1}}{{t}}\right)} \:={e}^{−{tlnt}} \:\rightarrow\mathrm{0}\:\left({t}\rightarrow+\infty\right) \\ $$$${t}^{{sin}\left(\frac{\mathrm{1}}{{t}}\right)} \:={e}^{{sin}\left(\frac{\mathrm{1}}{{t}}\right){ln}\left({t}\right)} \:\sim\:{e}^{\frac{{ln}\left({t}\right)}{{t}}} \rightarrow{e}^{\mathrm{0}} \:=\mathrm{1}\:\Rightarrow{lim}_{{t}\rightarrow+\infty} {g}\left({t}\right)=\mathrm{1}\:={lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right) \\ $$
Answered by john santu last updated on 25/Jan/20
![let :(sin x)^(1/x) +((1/x))^(sin x) = f(x)+g(x) lim_(x→0) f(x) =lim_(x→0) (sin x)^(1/x) = lim_(x→0) {(1+(sin x−1))^(1/(sin x−1)) }^((sin x−1)/x) = e^(lim_(x→0) [((sin x−1)/x)]) =e^(−∞) =0 lim_(x→0) g(x)=lim_(x→0) ((1/x))^(sin x) =lim_(x→0) (1+(((1−x)/x)))^(sin x) =e^(lim_(x→0) (sin x)) = e^0 = 1 therefore lim_(x→0) [(sin x)^(1/x) +((1/x))^(sin x) ] = 1](Q79445.png)
$${let}\::\left(\mathrm{sin}\:{x}\right)^{\frac{\mathrm{1}}{{x}}} +\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{sin}\:{x}} =\:{f}\left({x}\right)+{g}\left({x}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\left({x}\right)\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{sin}\:{x}\right)^{\frac{\mathrm{1}}{{x}}} = \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left\{\left(\mathrm{1}+\left(\mathrm{sin}\:{x}−\mathrm{1}\right)\right)^{\frac{\mathrm{1}}{\mathrm{sin}\:{x}−\mathrm{1}}} \right\}^{\frac{\mathrm{sin}\:{x}−\mathrm{1}}{{x}}} \\ $$$$=\:{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{\mathrm{sin}\:{x}−\mathrm{1}}{{x}}\right]} ={e}^{−\infty} =\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{g}\left({x}\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{sin}\:{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\left(\frac{\mathrm{1}−{x}}{{x}}\right)\right)^{\mathrm{sin}\:{x}} \\ $$$$={e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{sin}\:{x}\right)} =\:{e}^{\mathrm{0}} \:=\:\mathrm{1} \\ $$$${therefore}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\left(\mathrm{sin}\:{x}\right)^{\frac{\mathrm{1}}{{x}}} +\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{sin}\:{x}} \right]\:=\:\mathrm{1} \\ $$$$ \\ $$
