
Question Number 8490 by fernandodantas1996 last updated on 14/Oct/16
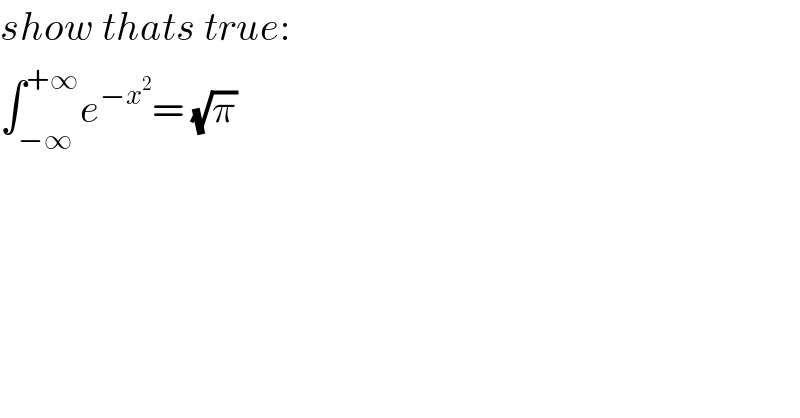
$${show}\:{thats}\:{true}: \\ $$$$\int_{−\infty} ^{+\infty} {e}^{−{x}^{\mathrm{2}} } =\:\sqrt{\pi} \\ $$
Commented by prakash jain last updated on 14/Oct/16
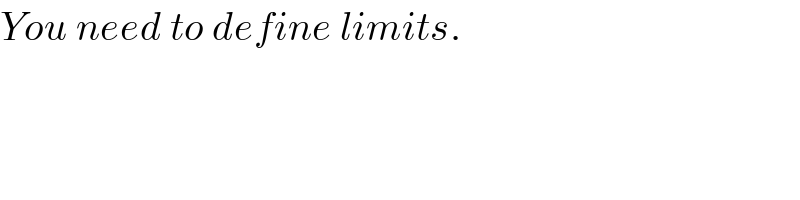
$${You}\:{need}\:{to}\:{define}\:{limits}. \\ $$
Commented by fernandodantas1996 last updated on 23/Oct/16

$$ \\ $$
Answered by prakash jain last updated on 23/Oct/16
![(∫_(−∞) ^∞ e^(−x^2 ) )^2 =∫_(−∞) ^∞ e^(−x^2 ) dx∫_(−∞) ^∞ e^(−y^2 ) dy =∫_(−∞) ^∞ ∫_(−∞) ^∞ e^(−(x^2 +y^2 )) dxdy Convert to polar coordinates x=rcos θ y=rsin θ dxdy=rdrdθ ∫_(−∞) ^∞ ∫_(−∞) ^∞ e^(−(x^2 +y^2 )) dxdy =∫_0 ^(2π) ∫_0 ^∞ e^(−r^2 ) rdrdθ =∫_0 ^(2π) dθ∫_0 ^∞ e^(−r^2 ) rdr subtitute s=−r^2 ⇒ds=−2rdr =∫_0 ^(2π) dθ∫_0 ^(−∞) −(1/2)e^s ds =2π((1/2))(−[e^(−∞) −e^0 ]) =π I=∫_(−∞) ^∞ e^(−x^2 ) dx I^2 =π⇒I=∫_(−∞) ^∞ e^(−x^2 ) dx=(√π)](Q8715.png)
$$\left(\int_{−\infty} ^{\infty} {e}^{−{x}^{\mathrm{2}} } \right)^{\mathrm{2}} =\int_{−\infty} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}\int_{−\infty} ^{\infty} {e}^{−{y}^{\mathrm{2}} } {dy} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int_{−\infty} ^{\infty} \int_{−\infty} ^{\infty} {e}^{−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)} {dxdy} \\ $$$$\mathrm{Convert}\:\mathrm{to}\:\mathrm{polar}\:\mathrm{coordinates} \\ $$$${x}={r}\mathrm{cos}\:\theta \\ $$$${y}={r}\mathrm{sin}\:\theta \\ $$$${dxdy}={rdrd}\theta \\ $$$$\int_{−\infty} ^{\infty} \int_{−\infty} ^{\infty} {e}^{−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)} {dxdy} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \int_{\mathrm{0}} ^{\infty} {e}^{−{r}^{\mathrm{2}} } {rdrd}\theta \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} {d}\theta\int_{\mathrm{0}} ^{\infty} {e}^{−{r}^{\mathrm{2}} } {rdr} \\ $$$$\mathrm{subtitute}\:{s}=−{r}^{\mathrm{2}} \Rightarrow{ds}=−\mathrm{2}{rdr} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} {d}\theta\int_{\mathrm{0}} ^{−\infty} −\frac{\mathrm{1}}{\mathrm{2}}{e}^{{s}} {ds} \\ $$$$=\mathrm{2}\pi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\left[{e}^{−\infty} −{e}^{\mathrm{0}} \right]\right) \\ $$$$=\pi \\ $$$${I}=\int_{−\infty} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx} \\ $$$${I}^{\mathrm{2}} =\pi\Rightarrow{I}=\int_{−\infty} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}=\sqrt{\pi} \\ $$
