Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 86003 by jagoll last updated on 26/Mar/20

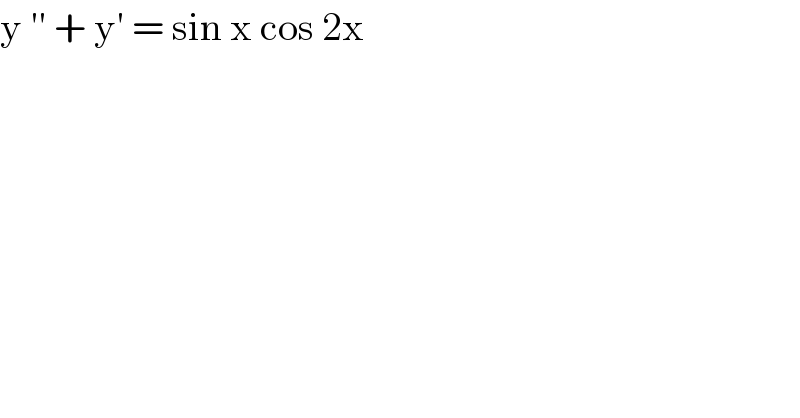
y ′′ + y′ = sin x cos 2x

$$\mathrm{y}\:''\:+\:\mathrm{y}'\:=\:\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{2x} \\ $$

Commented by mathmax by abdo last updated on 26/Mar/20

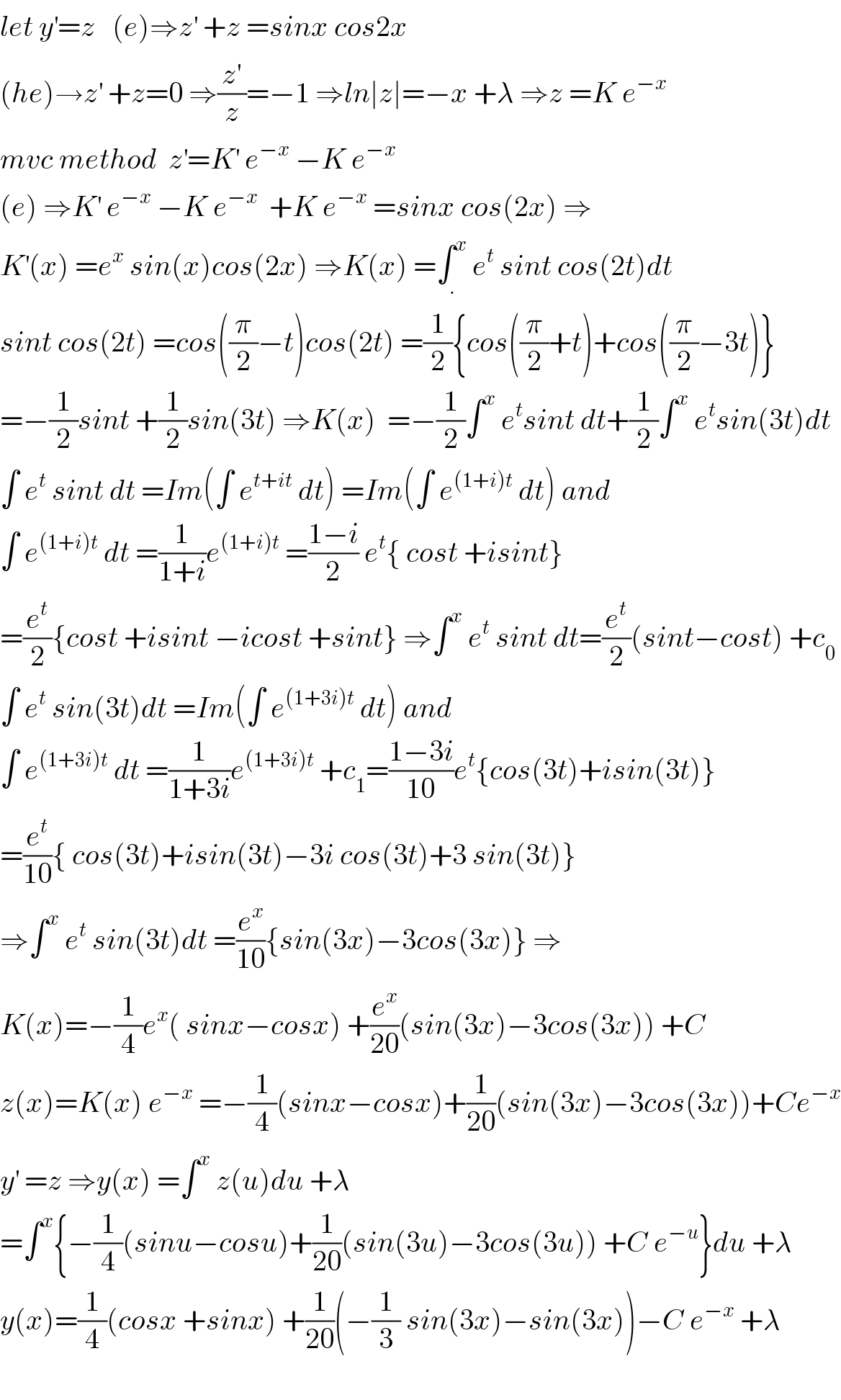
let y^′ =z (e)⇒z^′ +z =sinx cos2x (he)→z^′ +z=0 ⇒(z^′ /z)=−1 ⇒ln∣z∣=−x +λ ⇒z =K e^(−x) mvc method z^′ =K^′ e^(−x) −K e^(−x) (e) ⇒K^′ e^(−x) −K e^(−x) +K e^(−x) =sinx cos(2x) ⇒ K^′ (x) =e^x sin(x)cos(2x) ⇒K(x) =∫_. ^x e^t sint cos(2t)dt sint cos(2t) =cos((π/2)−t)cos(2t) =(1/2){cos((π/2)+t)+cos((π/2)−3t)} =−(1/2)sint +(1/2)sin(3t) ⇒K(x) =−(1/2)∫^x e^t sint dt+(1/2)∫^x e^t sin(3t)dt ∫ e^t sint dt =Im(∫ e^(t+it) dt) =Im(∫ e^((1+i)t) dt) and ∫ e^((1+i)t) dt =(1/(1+i))e^((1+i)t) =((1−i)/2) e^t { cost +isint} =(e^t /2){cost +isint −icost +sint} ⇒∫^x e^t sint dt=(e^t /2)(sint−cost) +c_0 ∫ e^t sin(3t)dt =Im(∫ e^((1+3i)t) dt) and ∫ e^((1+3i)t) dt =(1/(1+3i))e^((1+3i)t) +c_1 =((1−3i)/(10))e^t {cos(3t)+isin(3t)} =(e^t /(10)){ cos(3t)+isin(3t)−3i cos(3t)+3 sin(3t)} ⇒∫^x e^t sin(3t)dt =(e^x /(10)){sin(3x)−3cos(3x)} ⇒ K(x)=−(1/4)e^x ( sinx−cosx) +(e^x /(20))(sin(3x)−3cos(3x)) +C z(x)=K(x) e^(−x) =−(1/4)(sinx−cosx)+(1/(20))(sin(3x)−3cos(3x))+Ce^(−x) y^′ =z ⇒y(x) =∫^x z(u)du +λ =∫^x {−(1/4)(sinu−cosu)+(1/(20))(sin(3u)−3cos(3u)) +C e^(−u) }du +λ y(x)=(1/4)(cosx +sinx) +(1/(20))(−(1/3) sin(3x)−sin(3x))−C e^(−x) +λ

$${let}\:{y}^{'} ={z}\:\:\:\left({e}\right)\Rightarrow{z}^{'} \:+{z}\:={sinx}\:{cos}\mathrm{2}{x} \\ $$$$\left({he}\right)\rightarrow{z}^{'} \:+{z}=\mathrm{0}\:\Rightarrow\frac{{z}^{'} }{{z}}=−\mathrm{1}\:\Rightarrow{ln}\mid{z}\mid=−{x}\:+\lambda\:\Rightarrow{z}\:={K}\:{e}^{−{x}} \: \\ $$$${mvc}\:{method}\:\:{z}^{'} ={K}^{'} \:{e}^{−{x}} \:−{K}\:{e}^{−{x}} \\ $$$$\left({e}\right)\:\Rightarrow{K}^{'} \:{e}^{−{x}} \:−{K}\:{e}^{−{x}} \:\:+{K}\:{e}^{−{x}} \:={sinx}\:{cos}\left(\mathrm{2}{x}\right)\:\Rightarrow \\ $$$${K}^{'} \left({x}\right)\:={e}^{{x}} \:{sin}\left({x}\right){cos}\left(\mathrm{2}{x}\right)\:\Rightarrow{K}\left({x}\right)\:=\int_{.} ^{{x}} \:{e}^{{t}} \:{sint}\:{cos}\left(\mathrm{2}{t}\right){dt} \\ $$$${sint}\:{cos}\left(\mathrm{2}{t}\right)\:={cos}\left(\frac{\pi}{\mathrm{2}}−{t}\right){cos}\left(\mathrm{2}{t}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{{cos}\left(\frac{\pi}{\mathrm{2}}+{t}\right)+{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{3}{t}\right)\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{sint}\:+\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{3}{t}\right)\:\Rightarrow{K}\left({x}\right)\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\int^{{x}} \:{e}^{{t}} {sint}\:{dt}+\frac{\mathrm{1}}{\mathrm{2}}\int^{{x}} \:{e}^{{t}} {sin}\left(\mathrm{3}{t}\right){dt} \\ $$$$\int\:{e}^{{t}} \:{sint}\:{dt}\:={Im}\left(\int\:{e}^{{t}+{it}} \:{dt}\right)\:={Im}\left(\int\:{e}^{\left(\mathrm{1}+{i}\right){t}} \:{dt}\right)\:{and} \\ $$$$\int\:{e}^{\left(\mathrm{1}+{i}\right){t}} \:{dt}\:=\frac{\mathrm{1}}{\mathrm{1}+{i}}{e}^{\left(\mathrm{1}+{i}\right){t}} \:=\frac{\mathrm{1}−{i}}{\mathrm{2}}\:{e}^{{t}} \left\{\:{cost}\:+{isint}\right\} \\ $$$$=\frac{{e}^{{t}} }{\mathrm{2}}\left\{{cost}\:+{isint}\:−{icost}\:+{sint}\right\}\:\Rightarrow\int^{{x}} \:{e}^{{t}} \:{sint}\:{dt}=\frac{{e}^{{t}} }{\mathrm{2}}\left({sint}−{cost}\right)\:+{c}_{\mathrm{0}} \\ $$$$\int\:{e}^{{t}} \:{sin}\left(\mathrm{3}{t}\right){dt}\:={Im}\left(\int\:{e}^{\left(\mathrm{1}+\mathrm{3}{i}\right){t}} \:{dt}\right)\:{and}\: \\ $$$$\int\:{e}^{\left(\mathrm{1}+\mathrm{3}{i}\right){t}} \:{dt}\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{3}{i}}{e}^{\left(\mathrm{1}+\mathrm{3}{i}\right){t}} \:+{c}_{\mathrm{1}} =\frac{\mathrm{1}−\mathrm{3}{i}}{\mathrm{10}}{e}^{{t}} \left\{{cos}\left(\mathrm{3}{t}\right)+{isin}\left(\mathrm{3}{t}\right)\right\} \\ $$$$=\frac{{e}^{{t}} }{\mathrm{10}}\left\{\:{cos}\left(\mathrm{3}{t}\right)+{isin}\left(\mathrm{3}{t}\right)−\mathrm{3}{i}\:{cos}\left(\mathrm{3}{t}\right)+\mathrm{3}\:{sin}\left(\mathrm{3}{t}\right)\right\} \\ $$$$\Rightarrow\int^{{x}} \:{e}^{{t}} \:{sin}\left(\mathrm{3}{t}\right){dt}\:=\frac{{e}^{{x}} }{\mathrm{10}}\left\{{sin}\left(\mathrm{3}{x}\right)−\mathrm{3}{cos}\left(\mathrm{3}{x}\right)\right\}\:\Rightarrow \\ $$$${K}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{4}}{e}^{{x}} \left(\:{sinx}−{cosx}\right)\:+\frac{{e}^{{x}} }{\mathrm{20}}\left({sin}\left(\mathrm{3}{x}\right)−\mathrm{3}{cos}\left(\mathrm{3}{x}\right)\right)\:+{C} \\ $$$${z}\left({x}\right)={K}\left({x}\right)\:{e}^{−{x}} \:=−\frac{\mathrm{1}}{\mathrm{4}}\left({sinx}−{cosx}\right)+\frac{\mathrm{1}}{\mathrm{20}}\left({sin}\left(\mathrm{3}{x}\right)−\mathrm{3}{cos}\left(\mathrm{3}{x}\right)\right)+{Ce}^{−{x}} \\ $$$${y}^{'} \:={z}\:\Rightarrow{y}\left({x}\right)\:=\int^{{x}} \:{z}\left({u}\right){du}\:+\lambda \\ $$$$=\int^{{x}} \left\{−\frac{\mathrm{1}}{\mathrm{4}}\left({sinu}−{cosu}\right)+\frac{\mathrm{1}}{\mathrm{20}}\left({sin}\left(\mathrm{3}{u}\right)−\mathrm{3}{cos}\left(\mathrm{3}{u}\right)\right)\:+{C}\:{e}^{−{u}} \right\}{du}\:+\lambda \\ $$$${y}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left({cosx}\:+{sinx}\right)\:+\frac{\mathrm{1}}{\mathrm{20}}\left(−\frac{\mathrm{1}}{\mathrm{3}}\:{sin}\left(\mathrm{3}{x}\right)−{sin}\left(\mathrm{3}{x}\right)\right)−{C}\:{e}^{−{x}} \:+\lambda \\ $$$$ \\ $$

Answered by john santu last updated on 26/Mar/20

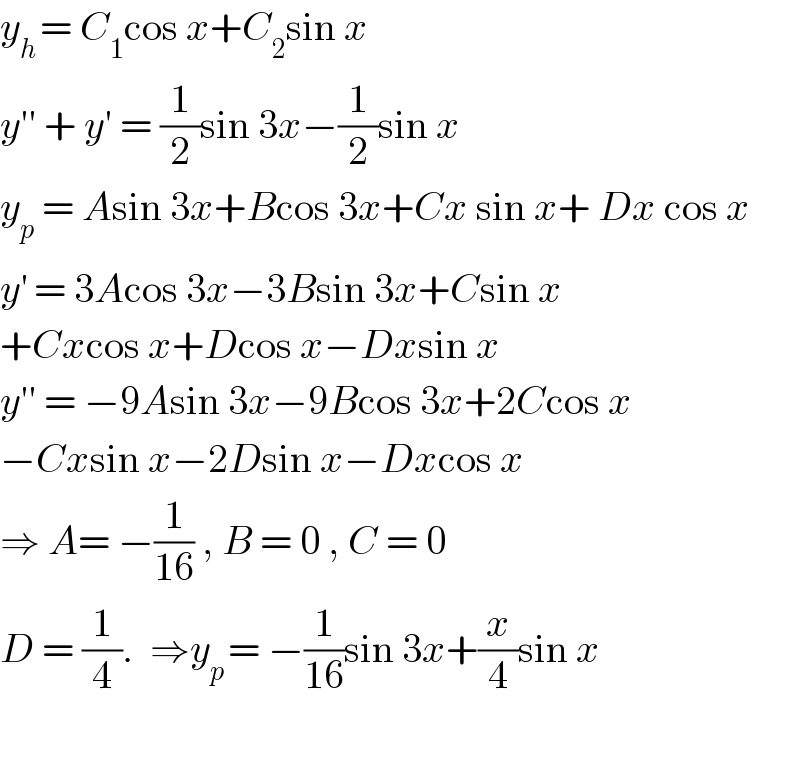
y_(h ) = C_1 cos x+C_2 sin x y′′ + y′ = (1/2)sin 3x−(1/2)sin x y_p = Asin 3x+Bcos 3x+Cx sin x+ Dx cos x y^′ = 3Acos 3x−3Bsin 3x+Csin x +Cxcos x+Dcos x−Dxsin x y′′ = −9Asin 3x−9Bcos 3x+2Ccos x −Cxsin x−2Dsin x−Dxcos x ⇒ A= −(1/(16)) , B = 0 , C = 0 D = (1/4). ⇒y_(p ) = −(1/(16))sin 3x+(x/4)sin x

$${y}_{{h}\:} =\:{C}_{\mathrm{1}} \mathrm{cos}\:{x}+{C}_{\mathrm{2}} \mathrm{sin}\:{x} \\ $$$${y}''\:+\:{y}'\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{3}{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:{x} \\ $$$${y}_{{p}} \:=\:{A}\mathrm{sin}\:\mathrm{3}{x}+{B}\mathrm{cos}\:\mathrm{3}{x}+{Cx}\:\mathrm{sin}\:{x}+\:{Dx}\:\mathrm{cos}\:{x} \\ $$$${y}^{'} \:=\:\mathrm{3}{A}\mathrm{cos}\:\mathrm{3}{x}−\mathrm{3}{B}\mathrm{sin}\:\mathrm{3}{x}+{C}\mathrm{sin}\:{x} \\ $$$$+{Cx}\mathrm{cos}\:{x}+{D}\mathrm{cos}\:{x}−{Dx}\mathrm{sin}\:{x} \\ $$$${y}''\:=\:−\mathrm{9}{A}\mathrm{sin}\:\mathrm{3}{x}−\mathrm{9}{B}\mathrm{cos}\:\mathrm{3}{x}+\mathrm{2}{C}\mathrm{cos}\:{x}\: \\ $$$$−{Cx}\mathrm{sin}\:{x}−\mathrm{2}{D}\mathrm{sin}\:{x}−{Dx}\mathrm{cos}\:{x} \\ $$$$\Rightarrow\:{A}=\:−\frac{\mathrm{1}}{\mathrm{16}}\:,\:{B}\:=\:\mathrm{0}\:,\:{C}\:=\:\mathrm{0} \\ $$$${D}\:=\:\frac{\mathrm{1}}{\mathrm{4}}.\:\:\Rightarrow{y}_{{p}\:} =\:−\frac{\mathrm{1}}{\mathrm{16}}\mathrm{sin}\:\mathrm{3}{x}+\frac{{x}}{\mathrm{4}}\mathrm{sin}\:{x} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com