Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 86406 by mathmax by abdo last updated on 28/Mar/20

let u^→ =i^→ −j^→ +k^→ and v^→ =2i^→ +j^→ +3k^→ (o,i,j,k) orthonormal 1) calculate ∣∣u^→ ∣∣ ,∣∣v^→ ∣∣ ,u^→ .v^→ 2) calculate cos(u^→ ,v^→ ) 3)calculate u^→ Λv^→ and sin(u^→ ,v^→ )

$${let}\:\:\overset{\rightarrow} {{u}}=\overset{\rightarrow} {{i}}−\overset{\rightarrow} {{j}}\:+\overset{\rightarrow} {{k}}\:{and}\:\overset{\rightarrow} {{v}}=\mathrm{2}\overset{\rightarrow} {{i}}+\overset{\rightarrow} {{j}}\:+\mathrm{3}\overset{\rightarrow} {{k}} \\ $$$$\left({o},{i},{j},{k}\right)\:{orthonormal} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\:\mid\mid\overset{\rightarrow} {{u}}\mid\mid\:\:,\mid\mid\overset{\rightarrow} {{v}}\mid\mid\:\:,\overset{\rightarrow} {{u}}.\overset{\rightarrow} {{v}} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{cos}\left(\overset{\rightarrow} {{u}},\overset{\rightarrow} {{v}}\right) \\ $$$$\left.\mathrm{3}\right){calculate}\:\overset{\rightarrow} {{u}}\Lambda\overset{\rightarrow} {{v}}\:\:\:\:{and}\:\:{sin}\left(\overset{\rightarrow} {{u}},\overset{\rightarrow} {{v}}\right) \\ $$

Answered by jagoll last updated on 28/Mar/20

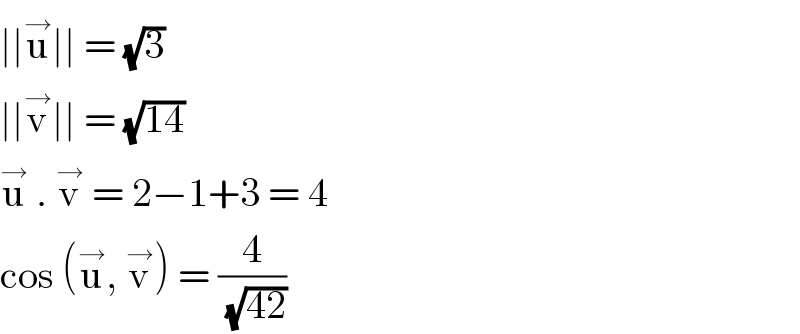
∣∣u^→ ∣∣ = (√3) ∣∣v^→ ∣∣ = (√(14)) u^→ . v^→ = 2−1+3 = 4 cos (u^→ , v^→ ) = (4/(√(42)))

$$\mid\mid\overset{\rightarrow} {\mathrm{u}}\mid\mid\:=\:\sqrt{\mathrm{3}} \\ $$$$\mid\mid\overset{\rightarrow} {\mathrm{v}}\mid\mid\:=\:\sqrt{\mathrm{14}} \\ $$$$\overset{\rightarrow} {\mathrm{u}}\:.\:\overset{\rightarrow} {\mathrm{v}}\:=\:\mathrm{2}−\mathrm{1}+\mathrm{3}\:=\:\mathrm{4} \\ $$$$\mathrm{cos}\:\left(\overset{\rightarrow} {\mathrm{u}},\:\overset{\rightarrow} {\mathrm{v}}\right)\:=\:\frac{\mathrm{4}}{\sqrt{\mathrm{42}}} \\ $$

Answered by Rio Michael last updated on 28/Mar/20

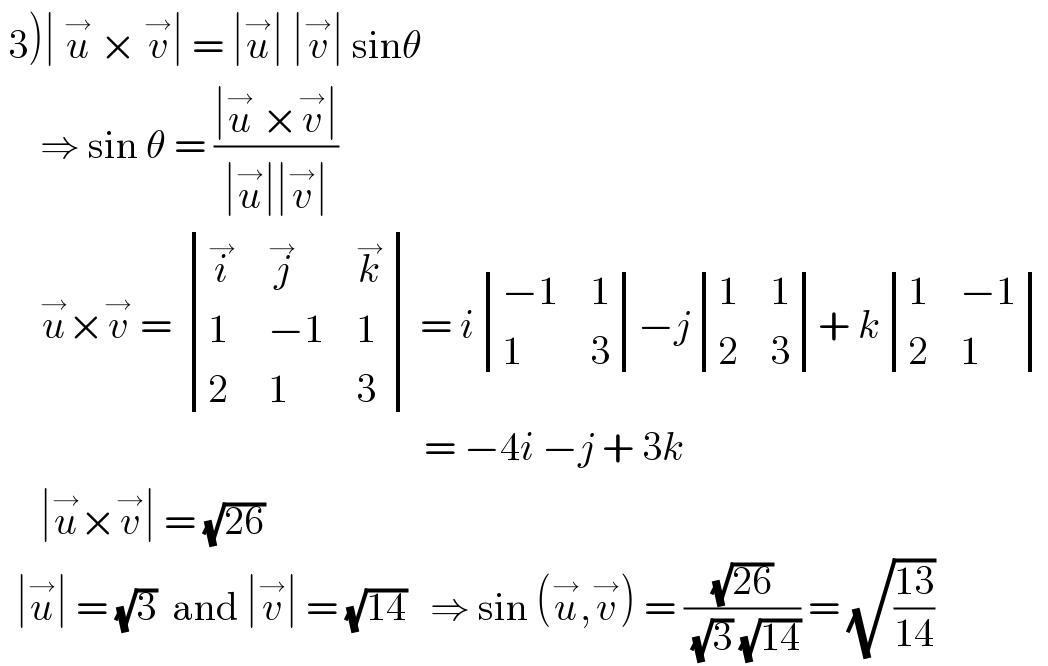
3)∣ u^→ × v^→ ∣ = ∣u^→ ∣ ∣v^→ ∣ sinθ ⇒ sin θ = ((∣u^→ ×v^→ ∣)/(∣u^→ ∣∣v^→ ∣)) u^→ ×v^→ = determinant ((i^→ ,j^→ ,k^→ ),(1,(−1),1),(2,1,3)) = i determinant (((−1),1),(1,3))−j determinant ((1,1),(2,3))+ k determinant ((1,(−1)),(2,1)) = −4i −j + 3k ∣u^→ ×v^→ ∣ = (√(26)) ∣u^→ ∣ = (√3) and ∣v^→ ∣ = (√(14)) ⇒ sin (u^→ ,v^→ ) = ((√(26))/((√3) (√(14)))) = (√((13)/(14)))

$$\left.\:\mathrm{3}\right)\mid\:\overset{\rightarrow} {{u}}\:×\:\overset{\rightarrow} {{v}}\mid\:=\:\mid\overset{\rightarrow} {{u}}\mid\:\mid\overset{\rightarrow} {{v}}\mid\:\mathrm{sin}\theta \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{sin}\:\theta\:=\:\frac{\mid\overset{\rightarrow} {{u}}\:×\overset{\rightarrow} {{v}}\mid}{\mid\overset{\rightarrow} {{u}}\mid\mid\overset{\rightarrow} {{v}}\mid} \\ $$$$\:\:\:\:\:\overset{\rightarrow} {{u}}×\overset{\rightarrow} {{v}}\:=\:\begin{vmatrix}{\overset{\rightarrow} {{i}}}&{\overset{\rightarrow} {{j}}}&{\overset{\rightarrow} {{k}}}\\{\mathrm{1}}&{−\mathrm{1}}&{\mathrm{1}}\\{\mathrm{2}}&{\mathrm{1}}&{\mathrm{3}}\end{vmatrix}\:=\:{i}\begin{vmatrix}{−\mathrm{1}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{3}}\end{vmatrix}−{j}\begin{vmatrix}{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{2}}&{\mathrm{3}}\end{vmatrix}+\:{k}\begin{vmatrix}{\mathrm{1}}&{−\mathrm{1}}\\{\mathrm{2}}&{\mathrm{1}}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{4}{i}\:−{j}\:+\:\mathrm{3}{k} \\ $$$$\:\:\:\:\:\mid\overset{\rightarrow} {{u}}×\overset{\rightarrow} {{v}}\mid\:=\:\sqrt{\mathrm{26}} \\ $$$$\:\:\mid\overset{\rightarrow} {{u}}\mid\:=\:\sqrt{\mathrm{3}}\:\:\mathrm{and}\:\mid\overset{\rightarrow} {{v}}\mid\:=\:\sqrt{\mathrm{14}}\:\:\:\Rightarrow\:\mathrm{sin}\:\left(\overset{\rightarrow} {{u}},\overset{\rightarrow} {{v}}\right)\:=\:\frac{\sqrt{\mathrm{26}}}{\sqrt{\mathrm{3}}\:\sqrt{\mathrm{14}}}\:=\:\sqrt{\frac{\mathrm{13}}{\mathrm{14}}} \\ $$

Commented by abdomathmax last updated on 28/Mar/20

thankx sir.

$${thankx}\:{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com