Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 86855 by jagoll last updated on 01/Apr/20

If a,b ,c are the roots of the equation x^3 +6x^2 −4x+3 = 0 . find the equation with roots a+b , b+c , a+c ?

$$\mathrm{If}\:\mathrm{a},\mathrm{b}\:,\mathrm{c}\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{6x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}\:=\:\mathrm{0}\:.\:\mathrm{find}\:\mathrm{the}\: \\ $$$$\mathrm{equation}\:\mathrm{with}\:\mathrm{roots}\:\mathrm{a}+\mathrm{b}\:,\:\mathrm{b}+\mathrm{c}\:,\:\mathrm{a}+\mathrm{c}\:? \\ $$

Answered by john santu last updated on 01/Apr/20

by vieta (i) a+b+c = −6 , ab+bc+ac = −4 abc =− 3 we seek p,q,r where x^3 +px^2 +qx+r =0 here we start p = −(2a+2b+2c) = 12 q = (a+b)(b+c)+(a+b)(a+c)+(b+c)(a+c) q = (−6−c)(−6−a)+(−6−c)(−6−b)+(−6−a)(−6−b) q = 36×3 −6(2a+2b+2c)+ab+ac+bc q = 108−72−4 = 32 r = (a+b)(b+c)(a+c) r = (−6−c)(−6−a)(−6−b) r = −(216+36(a+b+c)+6(ab+bc+ac)+abc) r = −(216+36(−6)+6(−4)−3) r = −27 so the required equation is x^3 +12x^2 +32x−27 =0

$$\mathrm{by}\:\mathrm{vieta}\: \\ $$$$\left(\mathrm{i}\right)\:\mathrm{a}+\mathrm{b}+\mathrm{c}\:=\:−\mathrm{6}\:,\:\mathrm{ab}+\mathrm{bc}+\mathrm{ac}\:=\:−\mathrm{4} \\ $$$$\mathrm{abc}\:=−\:\mathrm{3} \\ $$$$\mathrm{we}\:\mathrm{seek}\:\mathrm{p},\mathrm{q},\mathrm{r}\:\mathrm{where}\:\mathrm{x}^{\mathrm{3}} +\mathrm{px}^{\mathrm{2}} +\mathrm{qx}+\mathrm{r}\:=\mathrm{0} \\ $$$$\mathrm{here}\:\mathrm{we}\:\mathrm{start} \\ $$$$\mathrm{p}\:=\:−\left(\mathrm{2a}+\mathrm{2b}+\mathrm{2c}\right)\:=\:\mathrm{12} \\ $$$$\mathrm{q}\:=\:\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{b}+\mathrm{c}\right)+\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}+\mathrm{c}\right)+\left(\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{c}\right) \\ $$$$\mathrm{q}\:=\:\left(−\mathrm{6}−\mathrm{c}\right)\left(−\mathrm{6}−\mathrm{a}\right)+\left(−\mathrm{6}−\mathrm{c}\right)\left(−\mathrm{6}−\mathrm{b}\right)+\left(−\mathrm{6}−\mathrm{a}\right)\left(−\mathrm{6}−\mathrm{b}\right) \\ $$$$\mathrm{q}\:=\:\mathrm{36}×\mathrm{3}\:−\mathrm{6}\left(\mathrm{2a}+\mathrm{2b}+\mathrm{2c}\right)+\mathrm{ab}+\mathrm{ac}+\mathrm{bc} \\ $$$$\mathrm{q}\:=\:\mathrm{108}−\mathrm{72}−\mathrm{4}\:=\:\mathrm{32} \\ $$$$\mathrm{r}\:=\:\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}+\mathrm{c}\right)\: \\ $$$$\mathrm{r}\:=\:\left(−\mathrm{6}−\mathrm{c}\right)\left(−\mathrm{6}−\mathrm{a}\right)\left(−\mathrm{6}−\mathrm{b}\right) \\ $$$$\mathrm{r}\:=\:−\left(\mathrm{216}+\mathrm{36}\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)+\mathrm{6}\left(\mathrm{ab}+\mathrm{bc}+\mathrm{ac}\right)+\mathrm{abc}\right) \\ $$$$\mathrm{r}\:=\:−\left(\mathrm{216}+\mathrm{36}\left(−\mathrm{6}\right)+\mathrm{6}\left(−\mathrm{4}\right)−\mathrm{3}\right) \\ $$$$\mathrm{r}\:=\:−\mathrm{27} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{required}\:\mathrm{equation}\:\mathrm{is}\: \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{12x}^{\mathrm{2}} +\mathrm{32x}−\mathrm{27}\:=\mathrm{0}\: \\ $$$$ \\ $$

Commented by MJS last updated on 01/Apr/20

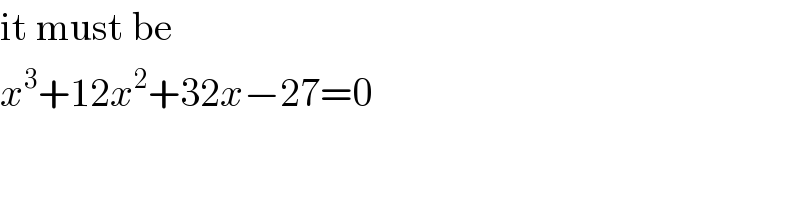
it must be x^3 +12x^2 +32x−27=0

$$\mathrm{it}\:\mathrm{must}\:\mathrm{be} \\ $$$${x}^{\mathrm{3}} +\mathrm{12}{x}^{\mathrm{2}} +\mathrm{32}{x}−\mathrm{27}=\mathrm{0} \\ $$

Commented by john santu last updated on 01/Apr/20

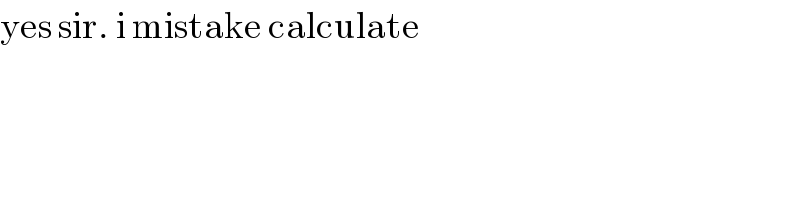
yes sir. i mistake calculate

$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{mistake}\:\mathrm{calculate} \\ $$

Commented by john santu last updated on 01/Apr/20

why x = t − (a/3) ?

$$\mathrm{why}\:\mathrm{x}\:=\:\mathrm{t}\:−\:\frac{\mathrm{a}}{\mathrm{3}}\:? \\ $$

Commented by jagoll last updated on 01/Apr/20

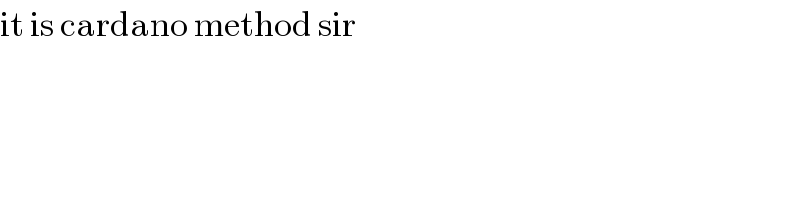
it is cardano method sir

$$\mathrm{it}\:\mathrm{is}\:\mathrm{cardano}\:\mathrm{method}\:\mathrm{sir} \\ $$

Commented by MJS last updated on 01/Apr/20

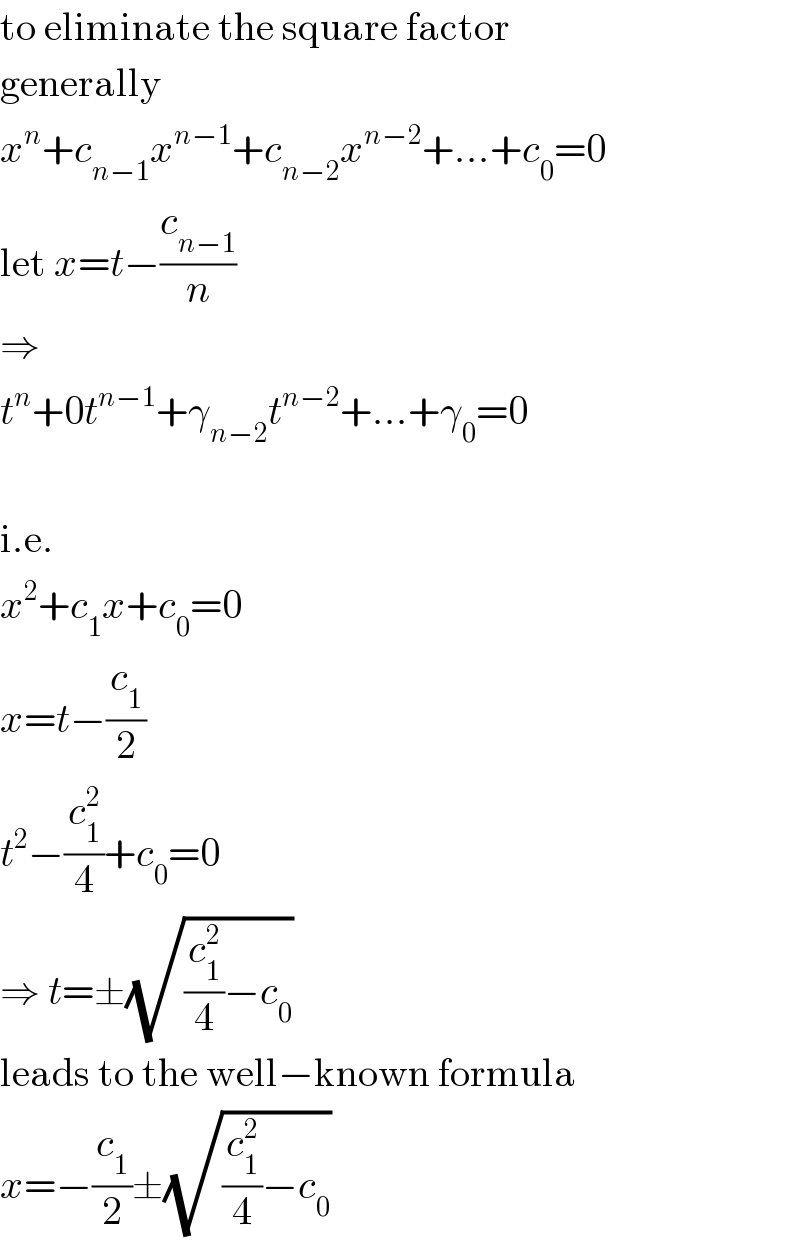
to eliminate the square factor generally x^n +c_(n−1) x^(n−1) +c_(n−2) x^(n−2) +...+c_0 =0 let x=t−(c_(n−1) /n) ⇒ t^n +0t^(n−1) +γ_(n−2) t^(n−2) +...+γ_0 =0 i.e. x^2 +c_1 x+c_0 =0 x=t−(c_1 /2) t^2 −(c_1 ^2 /4)+c_0 =0 ⇒ t=±(√((c_1 ^2 /4)−c_0 )) leads to the well−known formula x=−(c_1 /2)±(√((c_1 ^2 /4)−c_0 ))

$$\mathrm{to}\:\mathrm{eliminate}\:\mathrm{the}\:\mathrm{square}\:\mathrm{factor} \\ $$$$\mathrm{generally} \\ $$$${x}^{{n}} +{c}_{{n}−\mathrm{1}} {x}^{{n}−\mathrm{1}} +{c}_{{n}−\mathrm{2}} {x}^{{n}−\mathrm{2}} +...+{c}_{\mathrm{0}} =\mathrm{0} \\ $$$$\mathrm{let}\:{x}={t}−\frac{{c}_{{n}−\mathrm{1}} }{{n}} \\ $$$$\Rightarrow \\ $$$${t}^{{n}} +\mathrm{0}{t}^{{n}−\mathrm{1}} +\gamma_{{n}−\mathrm{2}} {t}^{{n}−\mathrm{2}} +...+\gamma_{\mathrm{0}} =\mathrm{0} \\ $$$$ \\ $$$$\mathrm{i}.\mathrm{e}. \\ $$$${x}^{\mathrm{2}} +{c}_{\mathrm{1}} {x}+{c}_{\mathrm{0}} =\mathrm{0} \\ $$$${x}={t}−\frac{{c}_{\mathrm{1}} }{\mathrm{2}} \\ $$$${t}^{\mathrm{2}} −\frac{{c}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{4}}+{c}_{\mathrm{0}} =\mathrm{0} \\ $$$$\Rightarrow\:{t}=\pm\sqrt{\frac{{c}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{4}}−{c}_{\mathrm{0}} } \\ $$$$\mathrm{leads}\:\mathrm{to}\:\mathrm{the}\:\mathrm{well}−\mathrm{known}\:\mathrm{formula} \\ $$$${x}=−\frac{{c}_{\mathrm{1}} }{\mathrm{2}}\pm\sqrt{\frac{{c}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{4}}−{c}_{\mathrm{0}} } \\ $$

Commented by MJS last updated on 01/Apr/20

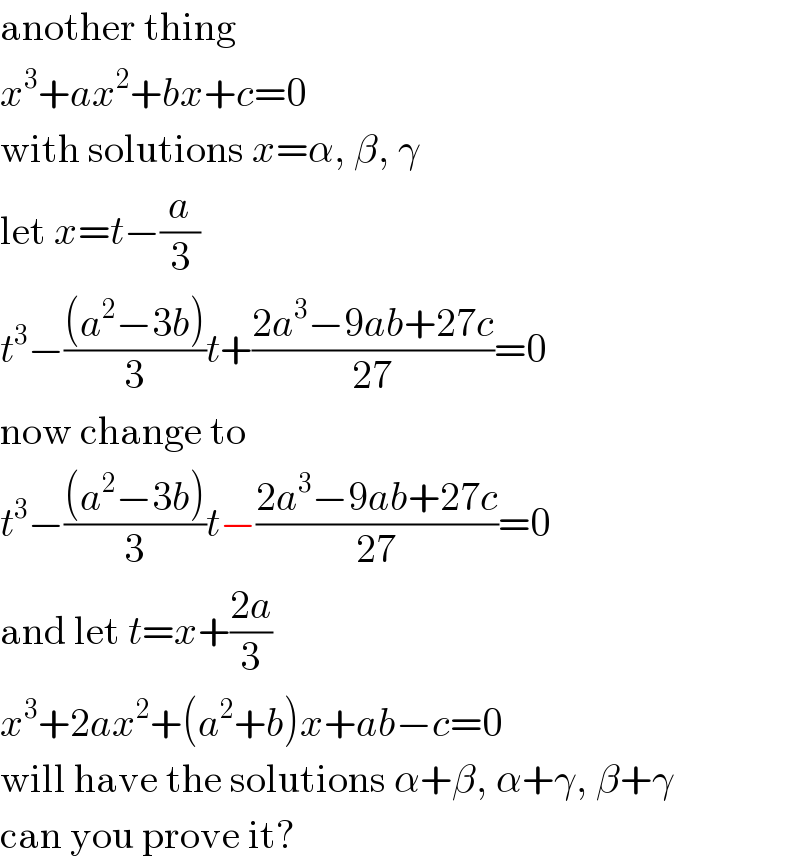
another thing x^3 +ax^2 +bx+c=0 with solutions x=α, β, γ let x=t−(a/3) t^3 −(((a^2 −3b))/3)t+((2a^3 −9ab+27c)/(27))=0 now change to t^3 −(((a^2 −3b))/3)t−((2a^3 −9ab+27c)/(27))=0 and let t=x+((2a)/3) x^3 +2ax^2 +(a^2 +b)x+ab−c=0 will have the solutions α+β, α+γ, β+γ can you prove it?

$$\mathrm{another}\:\mathrm{thing} \\ $$$${x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$$\mathrm{with}\:\mathrm{solutions}\:{x}=\alpha,\:\beta,\:\gamma \\ $$$$\mathrm{let}\:{x}={t}−\frac{{a}}{\mathrm{3}} \\ $$$${t}^{\mathrm{3}} −\frac{\left({a}^{\mathrm{2}} −\mathrm{3}{b}\right)}{\mathrm{3}}{t}+\frac{\mathrm{2}{a}^{\mathrm{3}} −\mathrm{9}{ab}+\mathrm{27}{c}}{\mathrm{27}}=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{change}\:\mathrm{to} \\ $$$${t}^{\mathrm{3}} −\frac{\left({a}^{\mathrm{2}} −\mathrm{3}{b}\right)}{\mathrm{3}}{t}−\frac{\mathrm{2}{a}^{\mathrm{3}} −\mathrm{9}{ab}+\mathrm{27}{c}}{\mathrm{27}}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{let}\:{t}={x}+\frac{\mathrm{2}{a}}{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} +\mathrm{2}{ax}^{\mathrm{2}} +\left({a}^{\mathrm{2}} +{b}\right){x}+{ab}−{c}=\mathrm{0} \\ $$$$\mathrm{will}\:\mathrm{have}\:\mathrm{the}\:\mathrm{solutions}\:\alpha+\beta,\:\alpha+\gamma,\:\beta+\gamma \\ $$$$\mathrm{can}\:\mathrm{you}\:\mathrm{prove}\:\mathrm{it}? \\ $$

Commented by john santu last updated on 01/Apr/20

waw....super sir

$$\mathrm{waw}....\mathrm{super}\:\mathrm{sir}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com