
Question Number 87014 by mathmax by abdo last updated on 01/Apr/20
![calculate ∫_0 ^∞ (e^(−[2x]) /((x+1)^2 ))dx](Q87014.png)
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\left[\mathrm{2}{x}\right]} }{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$
Commented by mathmax by abdo last updated on 02/Apr/20
![A =∫_0 ^∞ (e^(−[2x]) /((x+1)^2 ))dx ⇒A =_(2x=t) ∫_0 ^∞ (e^(−[t]) /(((t/2)+1)^2 ))(dt/2) =2 ∫_0 ^∞ (e^(−[t]) /((t+2)^2 ))dt =2Σ_(n=0) ^∞ ∫_n ^(n+1) (e^(−n) /((t+2)^2 ))dt =2Σ_(n=0) ^∞ e^(−n) [−(1/(t+2))]_n ^(n+1) =2 Σ_(n=0) ^∞ e^(−n) ((1/(n+2))−(1/(n+3))) =2 Σ_(n=0) ^∞ (e^(−n) /(n+2)) −2 Σ_(n=0) ^∞ (e^(−n) /(n+3)) we have Σ_(n=0) ^∞ (e^(−n) /(n+2)) =Σ_(n=2) ^∞ (e^(−(n−2)) /n) =e^2 Σ_(n=2) ^∞ (e^(−n) /n) Σ_(n=0) ^∞ (e^(−n) /(n+3)) =Σ_(n=3) ^∞ (e^(−(n−3)) /n) =e^3 Σ_(n=3) ^∞ (e^(−n) /n) also Σ_(n=2) ^∞ (e^(−n) /n) =Σ_(n=1) ^∞ (1/n)(e^(−1) )^n −e^(−1) =w(e^(−1) )−e^(−1) w(x)=Σ_(n=1) ^∞ (x^n /n) =−ln(1−x) ⇒Σ_(n=2) ^∞ (e^(−n) /n) =−ln(1−e^(−1) )−e^(−1) Σ_(n=3) ^∞ (e^(−n) /n) =−ln(1−e^(−1) )−e^(−1) −(e^(−2) /2) ⇒ A =2e^2 {−ln(1−e^(−1) )−e^(−1) }−2e^3 {−ln(1−e^(−1) )−e^(−1) −(e^(−2) /2)} =−2e^2 ln(1−e^(−1) )−2e +2e^3 ln(1−e^(−1) )+2e^2 +e =2(e^3 −e^2 )ln(1−e^(−1) ) +2e^2 −e](Q87081.png)
$${A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−\left[\mathrm{2}{x}\right]} }{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:\Rightarrow{A}\:=_{\mathrm{2}{x}={t}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\left[{t}\right]} }{\left(\frac{{t}}{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} }\frac{{dt}}{\mathrm{2}} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\left[{t}\right]} }{\left({t}+\mathrm{2}\right)^{\mathrm{2}} }{dt}\:=\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \:\int_{{n}} ^{{n}+\mathrm{1}} \:\frac{{e}^{−{n}} }{\left({t}+\mathrm{2}\right)^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \:{e}^{−{n}} \:\left[−\frac{\mathrm{1}}{{t}+\mathrm{2}}\right]_{{n}} ^{{n}+\mathrm{1}} \:=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{e}^{−{n}} \left(\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right) \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{e}^{−{n}} }{{n}+\mathrm{2}}\:−\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{e}^{−{n}} }{{n}+\mathrm{3}}\:\:{we}\:{have} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{e}^{−{n}} }{{n}+\mathrm{2}}\:=\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{{e}^{−\left({n}−\mathrm{2}\right)} }{{n}}\:={e}^{\mathrm{2}} \:\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{{e}^{−{n}} }{{n}} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{e}^{−{n}} }{{n}+\mathrm{3}}\:=\sum_{{n}=\mathrm{3}} ^{\infty} \:\frac{{e}^{−\left({n}−\mathrm{3}\right)} }{{n}}\:={e}^{\mathrm{3}} \:\sum_{{n}=\mathrm{3}} ^{\infty} \:\frac{{e}^{−{n}} }{{n}}\:\:\:{also} \\ $$$$\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{{e}^{−{n}} }{{n}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\left({e}^{−\mathrm{1}} \right)^{{n}} −{e}^{−\mathrm{1}} ={w}\left({e}^{−\mathrm{1}} \right)−{e}^{−\mathrm{1}} \: \\ $$$${w}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:=−{ln}\left(\mathrm{1}−{x}\right)\:\Rightarrow\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{{e}^{−{n}} }{{n}}\:=−{ln}\left(\mathrm{1}−{e}^{−\mathrm{1}} \right)−{e}^{−\mathrm{1}} \\ $$$$\sum_{{n}=\mathrm{3}} ^{\infty} \:\frac{{e}^{−{n}} }{{n}}\:=−{ln}\left(\mathrm{1}−{e}^{−\mathrm{1}} \right)−{e}^{−\mathrm{1}} −\frac{{e}^{−\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${A}\:=\mathrm{2}{e}^{\mathrm{2}} \left\{−{ln}\left(\mathrm{1}−{e}^{−\mathrm{1}} \right)−{e}^{−\mathrm{1}} \right\}−\mathrm{2}{e}^{\mathrm{3}} \left\{−{ln}\left(\mathrm{1}−{e}^{−\mathrm{1}} \right)−{e}^{−\mathrm{1}} −\frac{{e}^{−\mathrm{2}} }{\mathrm{2}}\right\} \\ $$$$=−\mathrm{2}{e}^{\mathrm{2}} {ln}\left(\mathrm{1}−{e}^{−\mathrm{1}} \right)−\mathrm{2}{e}\:+\mathrm{2}{e}^{\mathrm{3}} {ln}\left(\mathrm{1}−{e}^{−\mathrm{1}} \right)+\mathrm{2}{e}^{\mathrm{2}} \:+{e} \\ $$$$=\mathrm{2}\left({e}^{\mathrm{3}} −{e}^{\mathrm{2}} \right){ln}\left(\mathrm{1}−{e}^{−\mathrm{1}} \right)\:\:+\mathrm{2}{e}^{\mathrm{2}} \:−{e}\: \\ $$$$ \\ $$
Answered by M±th+et£s last updated on 01/Apr/20
![∫_0 ^∞ (e^(−[2x]) /((x+1)^2 ))dx =∫_0 ^(1/2) (1/((x+1)^2 ))dx + ∫_(1/2) ^1 (e^(−1) /((x+1)^2 ))dx + ∫_(1/2) ^1 (e^(−2) /((x+1)^2 ))+.....∞ =(1+(1/e)+(1/e^2 )+(1/e^3 )+....)∫_0 ^∞ (1/((x+1)^2 ))dx (e/(1−e))(1)=(e/(1−e)) .](Q87016.png)
$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\left[\mathrm{2}{x}\right]} }{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:+\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \frac{{e}^{−\mathrm{1}} }{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:+\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \frac{{e}^{−\mathrm{2}} }{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+.....\infty \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{1}}{{e}}+\frac{\mathrm{1}}{{e}^{\mathrm{2}} }+\frac{\mathrm{1}}{{e}^{\mathrm{3}} }+....\right)\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\frac{{e}}{\mathrm{1}−{e}}\left(\mathrm{1}\right)=\frac{{e}}{\mathrm{1}−{e}}\:. \\ $$
Commented by mathmax by abdo last updated on 02/Apr/20
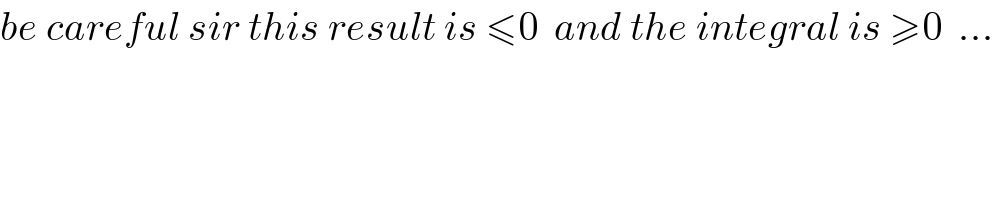
$${be}\:{careful}\:{sir}\:{this}\:{result}\:{is}\:\leqslant\mathrm{0}\:\:{and}\:{the}\:{integral}\:{is}\:\geqslant\mathrm{0}\:\:... \\ $$
Commented by M±th+et£s last updated on 02/Apr/20
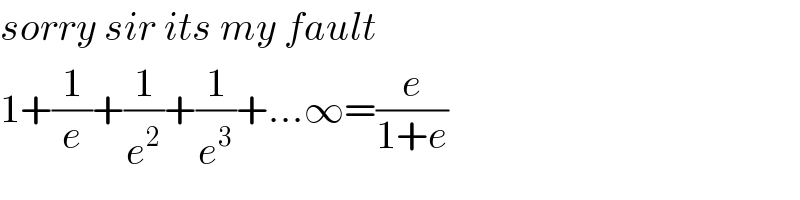
$${sorry}\:{sir}\:{its}\:{my}\:{fault} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{{e}}+\frac{\mathrm{1}}{{e}^{\mathrm{2}} }+\frac{\mathrm{1}}{{e}^{\mathrm{3}} }+...\infty=\frac{{e}}{\mathrm{1}+{e}} \\ $$
Commented by mathmax by abdo last updated on 02/Apr/20

$${nevermind}\:{sir}. \\ $$
Commented by M±th+et£s last updated on 02/Apr/20

$${thank}\:{you}\:{sir}\: \\ $$
