
Question Number 88245 by jagoll last updated on 09/Apr/20

Answered by john santu last updated on 09/Apr/20
![⇒(Δ/4) = 0 , [ Δ = discriminant ] (ab+bc)−(a^2 +b^2 )(b^2 +c^2 ) = 0 (a^2 b^2 +2ab^2 c+b^2 c^2 )−(a^2 b^2 +a^2 c+b^4 +b^2 c^2 ) =0 2ab^2 c−a^2 c^2 −b^4 = 0 (b^2 −ac)^2 = 0 ⇒ b^2 = ac r = (b/a) = (c/b) that prove these are in GP r = x. let r = (b/a) = (c/b) (a^2 +b^2 )r^2 − 2b(a+c)r + b^2 +c^2 = (a^2 +b^2 )((c/b))^2 −2b(a+c)((c/b))+ (b^2 +c^2 ) = (((ac)^2 )/b^2 ) + c^2 −2ac−c^2 +b^2 we know ac = b^2 , let substitute = (b^4 /b^2 ) +c^2 −2b^2 −c^2 +b^2 = b^2 −b^2 = 0 ⋮](Q88247.png)
$$\Rightarrow\frac{\Delta}{\mathrm{4}}\:=\:\mathrm{0}\:,\:\left[\:\Delta\:=\:{discriminant}\:\right] \\ $$$$\left({ab}+{bc}\right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\:=\:\mathrm{0} \\ $$$$\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{2}{ab}^{\mathrm{2}} {c}+{b}^{\mathrm{2}} {c}^{\mathrm{2}} \right)−\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}+{b}^{\mathrm{4}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} \right)\:=\mathrm{0} \\ $$$$\mathrm{2}{ab}^{\mathrm{2}} {c}−{a}^{\mathrm{2}} {c}^{\mathrm{2}} −{b}^{\mathrm{4}} \:=\:\mathrm{0} \\ $$$$\left({b}^{\mathrm{2}} −{ac}\right)^{\mathrm{2}} \:=\:\mathrm{0}\:\Rightarrow\:{b}^{\mathrm{2}} \:=\:{ac}\: \\ $$$${r}\:=\:\frac{{b}}{{a}}\:=\:\frac{{c}}{{b}} \\ $$$${that}\:{prove}\:{these}\:{are}\:{in}\:{GP} \\ $$$${r}\:=\:{x}.\:{let}\:{r}\:=\:\frac{{b}}{{a}}\:=\:\frac{{c}}{{b}} \\ $$$$\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){r}^{\mathrm{2}} \:−\:\mathrm{2}{b}\left({a}+{c}\right){r}\:+\:{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$$=\:\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\frac{{c}}{{b}}\right)^{\mathrm{2}} −\mathrm{2}{b}\left({a}+{c}\right)\left(\frac{{c}}{{b}}\right)+ \\ $$$$\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\: \\ $$$$=\:\frac{\left({ac}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:+\:{c}^{\mathrm{2}} −\mathrm{2}{ac}−{c}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$${we}\:{know}\:{ac}\:=\:{b}^{\mathrm{2}} \:,\:{let}\:{substitute} \\ $$$$=\:\frac{{b}^{\mathrm{4}} }{{b}^{\mathrm{2}} }\:+{c}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} −{c}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$=\:{b}^{\mathrm{2}} −{b}^{\mathrm{2}} \:=\:\mathrm{0}\:\vdots \\ $$$$ \\ $$
Commented by jagoll last updated on 09/Apr/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by $@ty@m123 last updated on 09/Apr/20
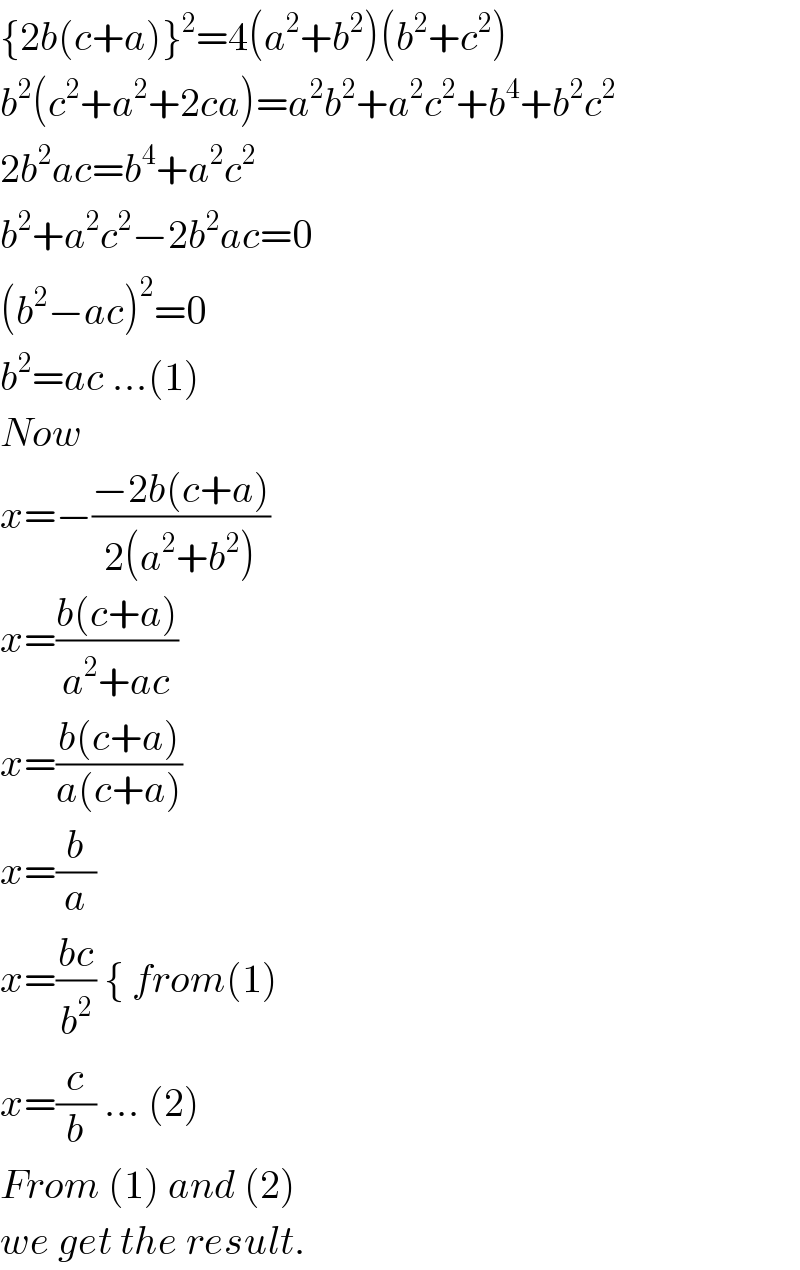
$$\left\{\mathrm{2}{b}\left({c}+{a}\right)\right\}^{\mathrm{2}} =\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$${b}^{\mathrm{2}} \left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} +\mathrm{2}{ca}\right)={a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{4}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} \\ $$$$\mathrm{2}{b}^{\mathrm{2}} {ac}={b}^{\mathrm{4}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} {ac}=\mathrm{0} \\ $$$$\left({b}^{\mathrm{2}} −{ac}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${b}^{\mathrm{2}} ={ac}\:...\left(\mathrm{1}\right) \\ $$$${Now}\: \\ $$$${x}=−\frac{−\mathrm{2}{b}\left({c}+{a}\right)}{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)} \\ $$$${x}=\frac{{b}\left({c}+{a}\right)}{{a}^{\mathrm{2}} +{ac}} \\ $$$${x}=\frac{{b}\left({c}+{a}\right)}{{a}\left({c}+{a}\right)} \\ $$$${x}=\frac{{b}}{{a}} \\ $$$${x}=\frac{{bc}}{{b}^{\mathrm{2}} }\:\left\{\:{from}\left(\mathrm{1}\right)\right. \\ $$$${x}=\frac{{c}}{{b}}\:...\:\left(\mathrm{2}\right) \\ $$$${From}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right) \\ $$$${we}\:{get}\:{the}\:{result}. \\ $$
Commented by jagoll last updated on 09/Apr/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
