Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 88580 by jagoll last updated on 11/Apr/20

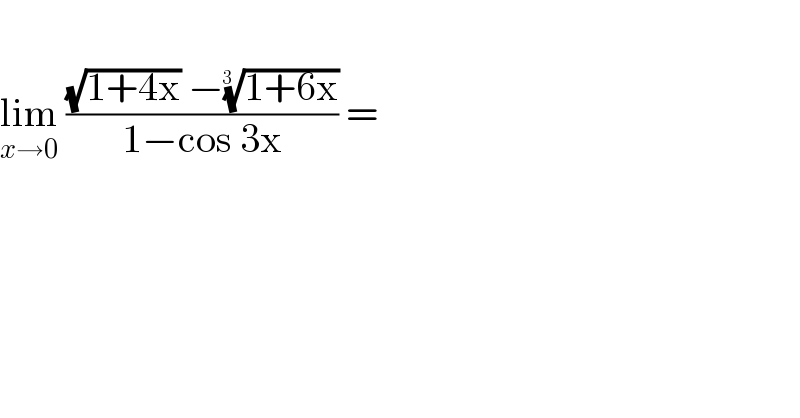
lim_(x→0) (((√(1+4x)) −((1+6x))^(1/(3 )) )/(1−cos 3x)) =

$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+\mathrm{4x}}\:−\sqrt[{\mathrm{3}\:\:}]{\mathrm{1}+\mathrm{6x}}}{\mathrm{1}−\mathrm{cos}\:\mathrm{3x}}\:= \\ $$

Commented by mathmax by abdo last updated on 11/Apr/20

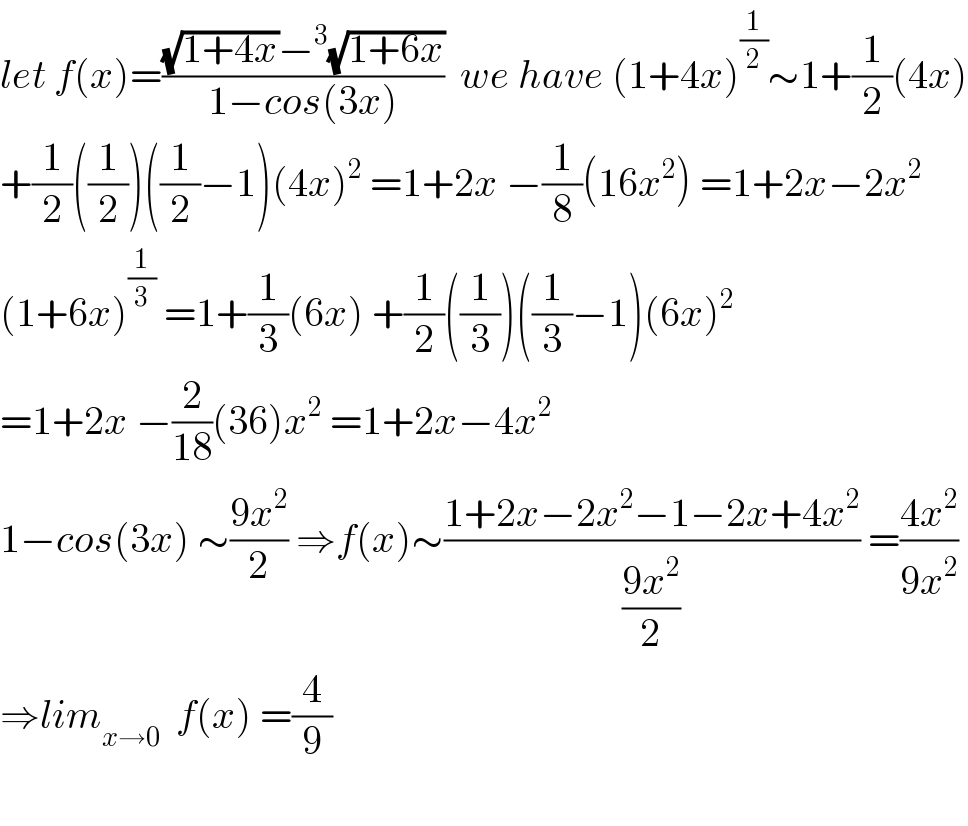
let f(x)=(((√(1+4x))−^3 (√(1+6x)))/(1−cos(3x))) we have (1+4x)^(1/2) ∼1+(1/2)(4x) +(1/2)((1/2))((1/2)−1)(4x)^2 =1+2x −(1/8)(16x^2 ) =1+2x−2x^2 (1+6x)^(1/3) =1+(1/3)(6x) +(1/2)((1/3))((1/3)−1)(6x)^2 =1+2x −(2/(18))(36)x^2 =1+2x−4x^2 1−cos(3x) ∼((9x^2 )/2) ⇒f(x)∼((1+2x−2x^2 −1−2x+4x^2 )/((9x^2 )/2)) =((4x^2 )/(9x^2 )) ⇒lim_(x→0) f(x) =(4/9)

$${let}\:{f}\left({x}\right)=\frac{\sqrt{\mathrm{1}+\mathrm{4}{x}}−^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{6}{x}}}{\mathrm{1}−{cos}\left(\mathrm{3}{x}\right)}\:\:{we}\:{have}\:\left(\mathrm{1}+\mathrm{4}{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \sim\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}{x}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{4}{x}\right)^{\mathrm{2}} \:=\mathrm{1}+\mathrm{2}{x}\:−\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{16}{x}^{\mathrm{2}} \right)\:=\mathrm{1}+\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\mathrm{6}{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{6}{x}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right)\left(\mathrm{6}{x}\right)^{\mathrm{2}} \\ $$$$=\mathrm{1}+\mathrm{2}{x}\:−\frac{\mathrm{2}}{\mathrm{18}}\left(\mathrm{36}\right){x}^{\mathrm{2}} \:=\mathrm{1}+\mathrm{2}{x}−\mathrm{4}{x}^{\mathrm{2}} \\ $$$$\mathrm{1}−{cos}\left(\mathrm{3}{x}\right)\:\sim\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow{f}\left({x}\right)\sim\frac{\mathrm{1}+\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}−\mathrm{2}{x}+\mathrm{4}{x}^{\mathrm{2}} }{\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}}\:=\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{9}{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:{f}\left({x}\right)\:=\frac{\mathrm{4}}{\mathrm{9}} \\ $$$$ \\ $$

Commented by jagoll last updated on 11/Apr/20

i got 0. it correct?

$$\mathrm{i}\:\mathrm{got}\:\mathrm{0}.\:\mathrm{it}\:\mathrm{correct}? \\ $$

Commented by jagoll last updated on 11/Apr/20

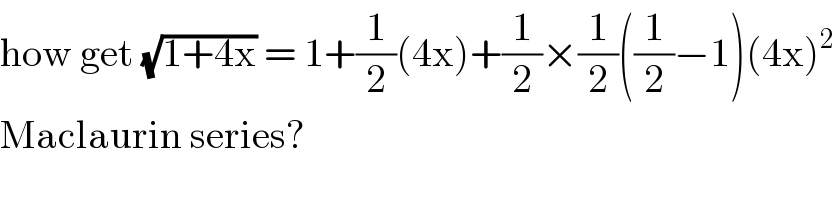
how get (√(1+4x)) = 1+(1/2)(4x)+(1/2)×(1/2)((1/2)−1)(4x)^2 Maclaurin series?

$$\mathrm{how}\:\mathrm{get}\:\sqrt{\mathrm{1}+\mathrm{4x}}\:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4x}\right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{4x}\right)^{\mathrm{2}} \\ $$$$\mathrm{Maclaurin}\:\mathrm{series}? \\ $$

Commented by mathmax by abdo last updated on 11/Apr/20

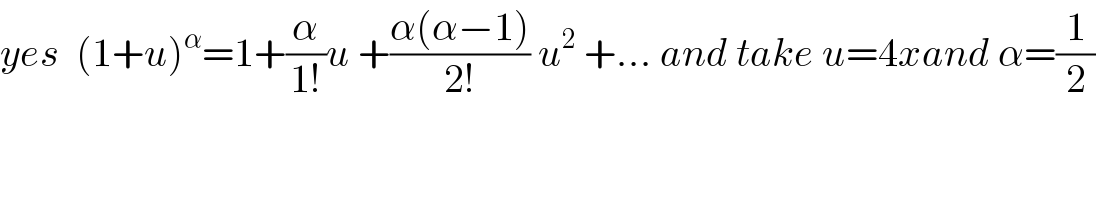
yes (1+u)^α =1+(α/(1!))u +((α(α−1))/(2!)) u^2 +... and take u=4xand α=(1/2)

$${yes}\:\:\left(\mathrm{1}+{u}\right)^{\alpha} =\mathrm{1}+\frac{\alpha}{\mathrm{1}!}{u}\:+\frac{\alpha\left(\alpha−\mathrm{1}\right)}{\mathrm{2}!}\:{u}^{\mathrm{2}} \:+...\:{and}\:{take}\:{u}=\mathrm{4}{xand}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com