Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 8865 by 7C;00 last updated on 03/Nov/16

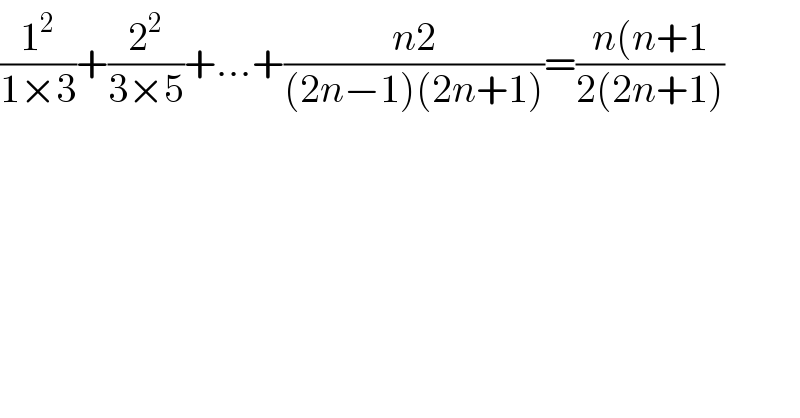
(1^2 /(1×3))+(2^2 /(3×5))+...+((n2)/((2n−1)(2n+1)))=((n(n+1)/(2(2n+1)))

$$\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{1}×\mathrm{3}}+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{3}×\mathrm{5}}+...+\frac{{n}\mathrm{2}}{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}=\frac{{n}\left({n}+\mathrm{1}\right.}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$

Answered by nume1114 last updated on 04/Nov/16

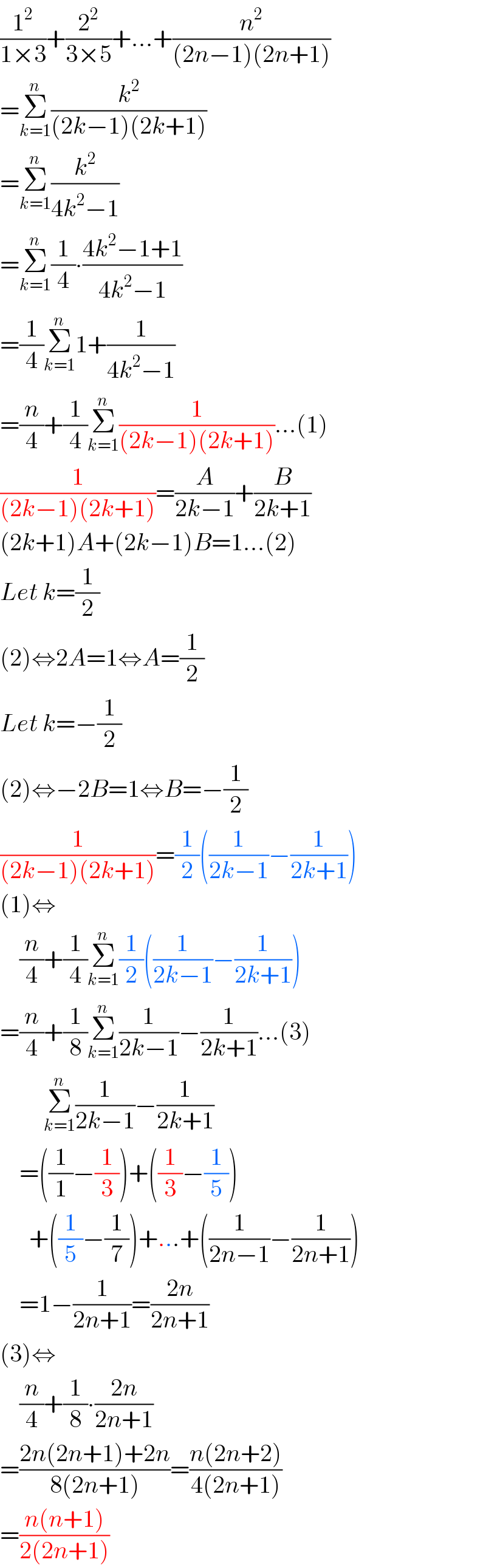
(1^2 /(1×3))+(2^2 /(3×5))+...+(n^2 /((2n−1)(2n+1))) =Σ_(k=1) ^n (k^2 /((2k−1)(2k+1))) =Σ_(k=1) ^n (k^2 /(4k^2 −1)) =Σ_(k=1) ^n (1/4)∙((4k^2 −1+1)/(4k^2 −1)) =(1/4)Σ_(k=1) ^n 1+(1/(4k^2 −1)) =(n/4)+(1/4)Σ_(k=1) ^n (1/((2k−1)(2k+1)))...(1) (1/((2k−1)(2k+1)))=(A/(2k−1))+(B/(2k+1)) (2k+1)A+(2k−1)B=1...(2) Let k=(1/2) (2)⇔2A=1⇔A=(1/2) Let k=−(1/2) (2)⇔−2B=1⇔B=−(1/2) (1/((2k−1)(2k+1)))=(1/2)((1/(2k−1))−(1/(2k+1))) (1)⇔ (n/4)+(1/4)Σ_(k=1) ^n (1/2)((1/(2k−1))−(1/(2k+1))) =(n/4)+(1/8)Σ_(k=1) ^n (1/(2k−1))−(1/(2k+1))...(3) Σ_(k=1) ^n (1/(2k−1))−(1/(2k+1)) =((1/1)−(1/3))+((1/3)−(1/5)) +((1/5)−(1/7))+...+((1/(2n−1))−(1/(2n+1))) =1−(1/(2n+1))=((2n)/(2n+1)) (3)⇔ (n/4)+(1/8)∙((2n)/(2n+1)) =((2n(2n+1)+2n)/(8(2n+1)))=((n(2n+2))/(4(2n+1))) =((n(n+1))/(2(2n+1)))

$$\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{1}×\mathrm{3}}+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{3}×\mathrm{5}}+...+\frac{{n}^{\mathrm{2}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{2}} }{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{2}} }{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{4}}\centerdot\frac{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{{n}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}...\left(\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}=\frac{{A}}{\mathrm{2}{k}−\mathrm{1}}+\frac{{B}}{\mathrm{2}{k}+\mathrm{1}} \\ $$$$\left(\mathrm{2}{k}+\mathrm{1}\right){A}+\left(\mathrm{2}{k}−\mathrm{1}\right){B}=\mathrm{1}...\left(\mathrm{2}\right) \\ $$$${Let}\:{k}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\Leftrightarrow\mathrm{2}{A}=\mathrm{1}\Leftrightarrow{A}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${Let}\:{k}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\Leftrightarrow−\mathrm{2}{B}=\mathrm{1}\Leftrightarrow{B}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\right) \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow \\ $$$$\:\:\:\:\frac{{n}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\right) \\ $$$$=\frac{{n}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}...\left(\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}} \\ $$$$\:\:\:\:=\left(\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$$\:\:\:\:\:\:+\left(\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}\right)+...+\left(\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right) \\ $$$$\:\:\:\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}=\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\left(\mathrm{3}\right)\Leftrightarrow \\ $$$$\:\:\:\:\frac{{n}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}\centerdot\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{2}{n}\left(\mathrm{2}{n}+\mathrm{1}\right)+\mathrm{2}{n}}{\mathrm{8}\left(\mathrm{2}{n}+\mathrm{1}\right)}=\frac{{n}\left(\mathrm{2}{n}+\mathrm{2}\right)}{\mathrm{4}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com