Question Number 90252 by ajfour last updated on 22/Apr/20
Commented by ajfour last updated on 22/Apr/20

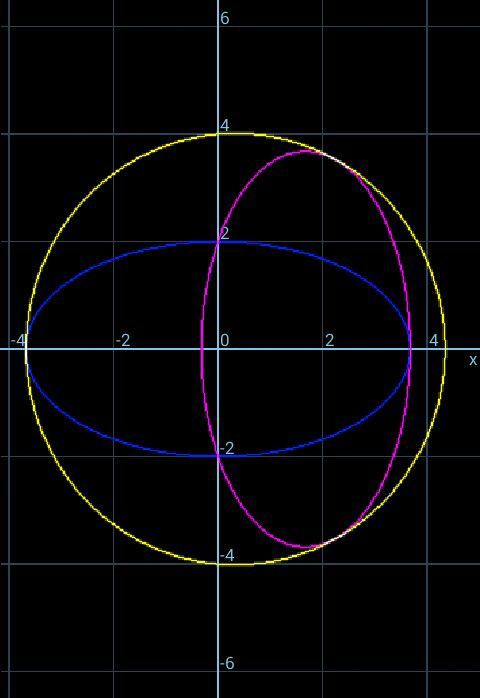
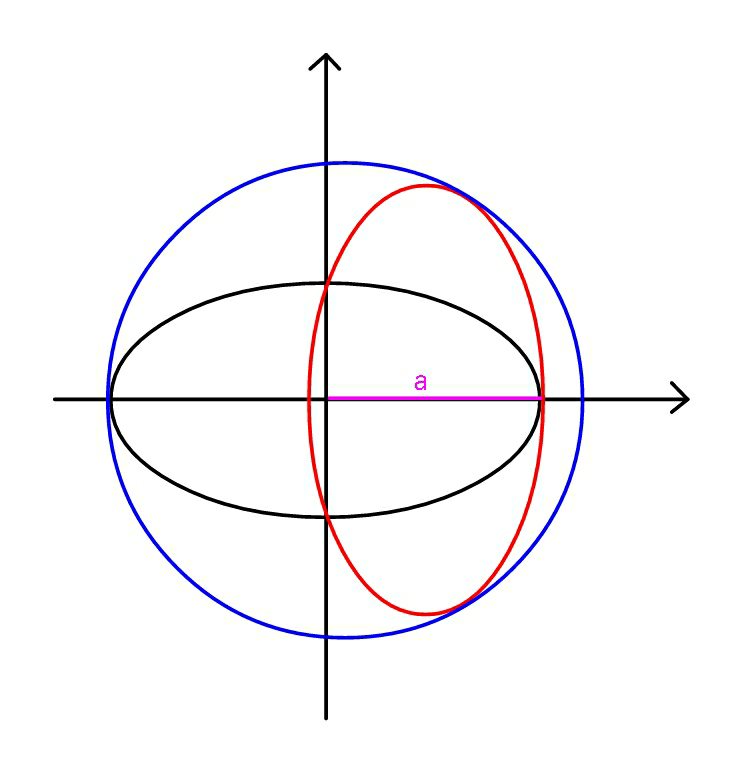
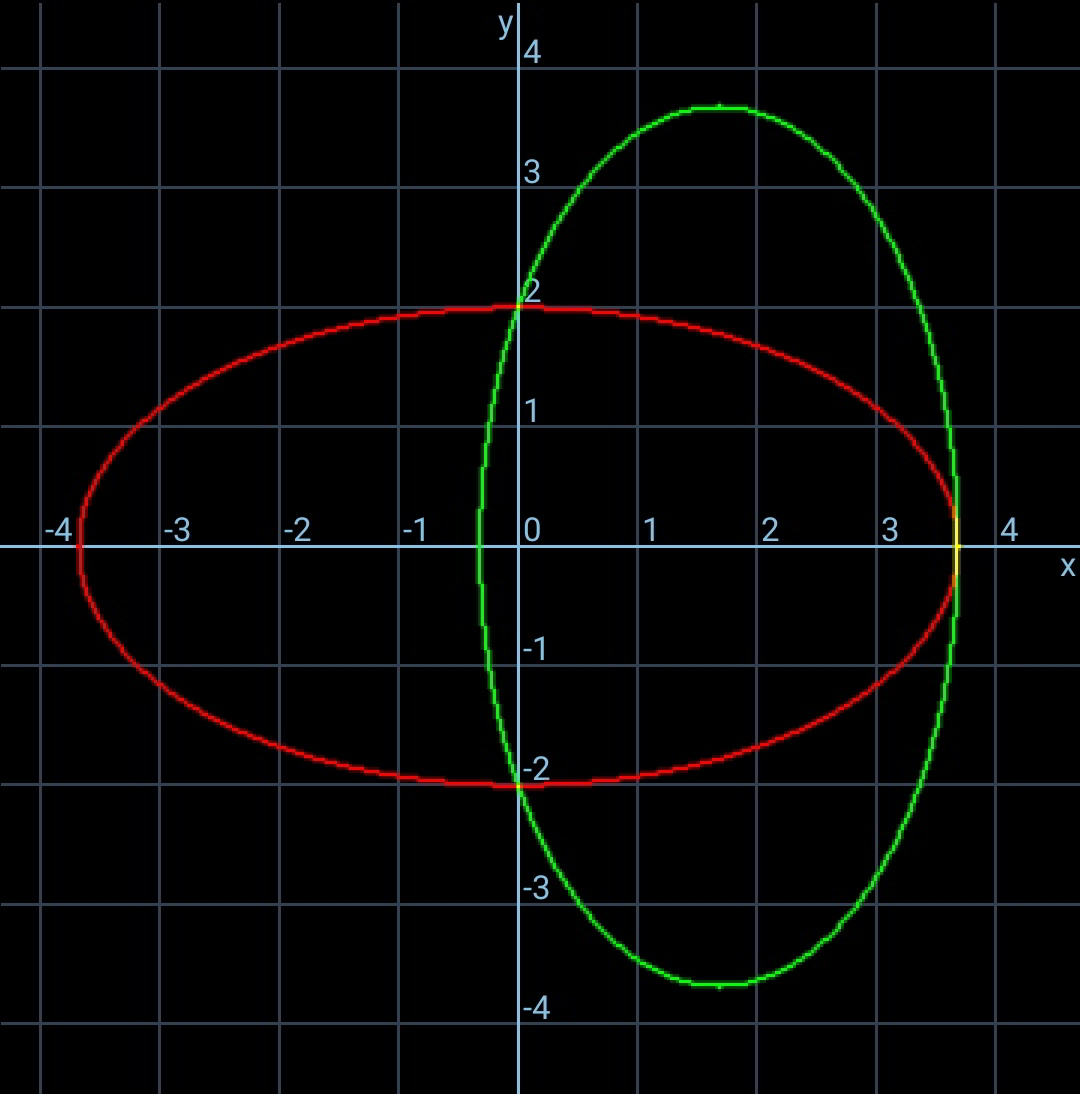
$${If}\:{both}\:{ellipses}\:{have}\:{the}\:{same} \\ $$$${shape},\:{find},\:{b}/{a}\:.{Also}\:{find} \\ $$$${circumradius}\:{in}\:{terms}\:{of}\:{a}. \\ $$
Answered by ajfour last updated on 22/Apr/20
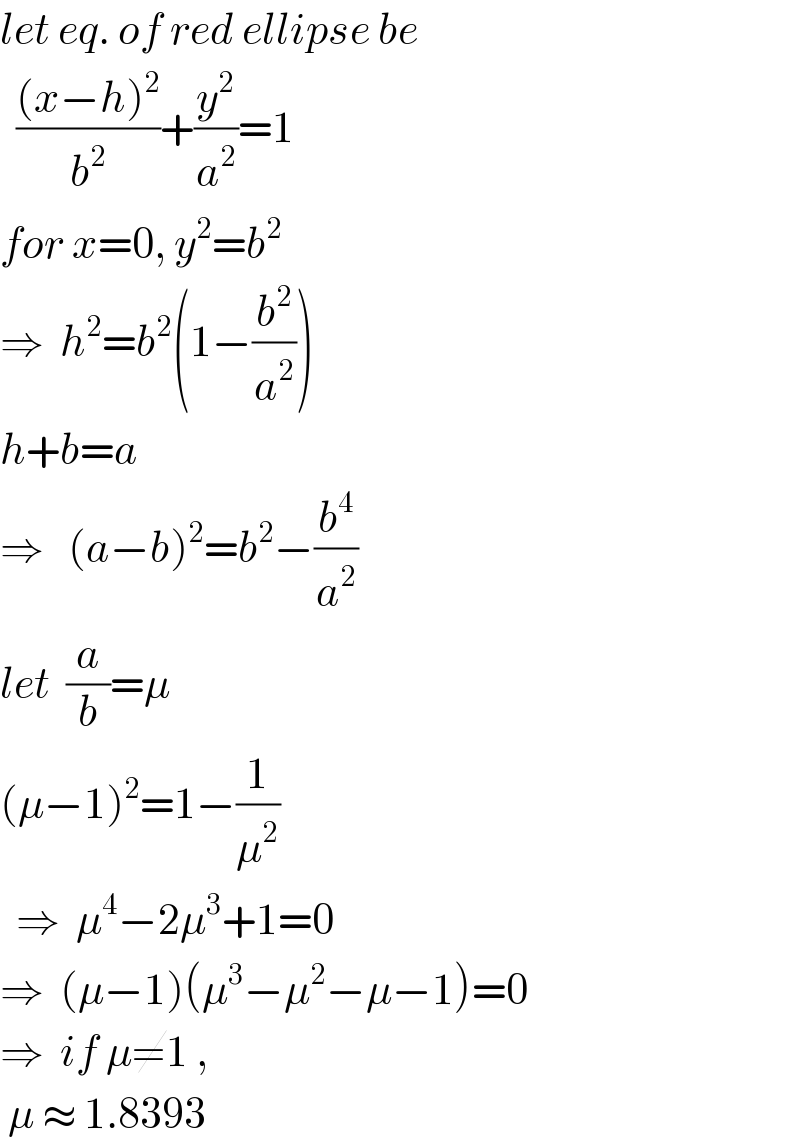
$${let}\:{eq}.\:{of}\:{red}\:{ellipse}\:{be} \\ $$$$\:\:\frac{\left({x}−{h}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\mathrm{1} \\ $$$${for}\:{x}=\mathrm{0},\:{y}^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{h}^{\mathrm{2}} ={b}^{\mathrm{2}} \left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$${h}+{b}={a} \\ $$$$\Rightarrow\:\:\:\left({a}−{b}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} −\frac{{b}^{\mathrm{4}} }{{a}^{\mathrm{2}} } \\ $$$${let}\:\:\frac{{a}}{{b}}=\mu \\ $$$$\left(\mu−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1}−\frac{\mathrm{1}}{\mu^{\mathrm{2}} } \\ $$$$\:\:\Rightarrow\:\:\mu^{\mathrm{4}} −\mathrm{2}\mu^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\left(\mu−\mathrm{1}\right)\left(\mu^{\mathrm{3}} −\mu^{\mathrm{2}} −\mu−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:{if}\:\mu\neq\mathrm{1}\:,\: \\ $$$$\:\mu\:\approx\:\mathrm{1}.\mathrm{8393} \\ $$
Commented by mr W last updated on 22/Apr/20
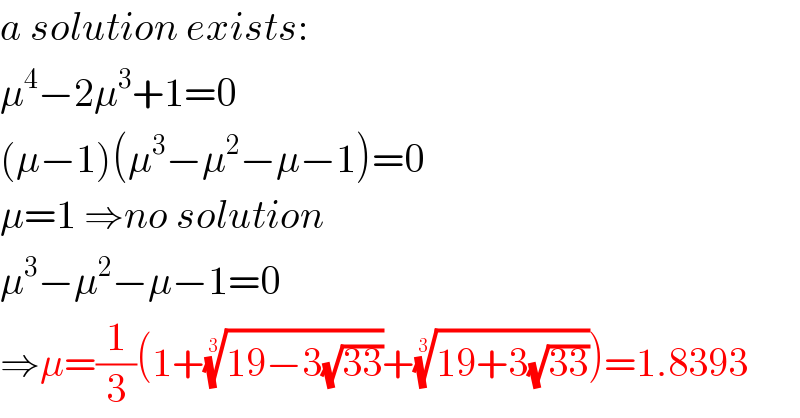
$${a}\:{solution}\:{exists}: \\ $$$$\mu^{\mathrm{4}} −\mathrm{2}\mu^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$$\left(\mu−\mathrm{1}\right)\left(\mu^{\mathrm{3}} −\mu^{\mathrm{2}} −\mu−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mu=\mathrm{1}\:\Rightarrow{no}\:{solution} \\ $$$$\mu^{\mathrm{3}} −\mu^{\mathrm{2}} −\mu−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mu=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{19}−\mathrm{3}\sqrt{\mathrm{33}}}+\sqrt[{\mathrm{3}}]{\mathrm{19}+\mathrm{3}\sqrt{\mathrm{33}}}\right)=\mathrm{1}.\mathrm{8393} \\ $$
Commented by mr W last updated on 22/Apr/20
Commented by ajfour last updated on 22/Apr/20
$${yes}\:{sir},\:\mu\approx\:\mathrm{1}.\mathrm{8393}\:,\:{thanks}, \\ $$$${can}\:{we}\:{try}\:{the}\:{second}\:{part}\:{then} \\ $$
Answered by ajfour last updated on 22/Apr/20
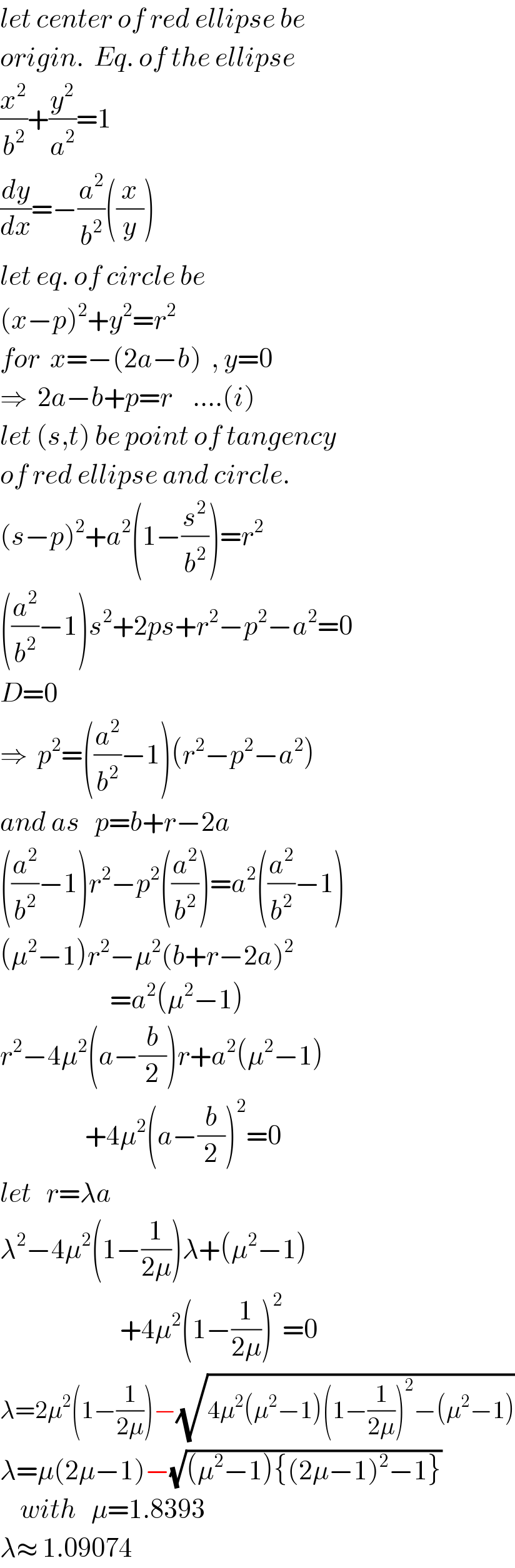
$${let}\:{center}\:{of}\:{red}\:{ellipse}\:{be}\: \\ $$$${origin}.\:\:{Eq}.\:{of}\:{the}\:{ellipse} \\ $$$$\frac{{x}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{dy}}{{dx}}=−\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\left(\frac{{x}}{{y}}\right) \\ $$$${let}\:{eq}.\:{of}\:{circle}\:{be} \\ $$$$\left({x}−{p}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${for}\:\:{x}=−\left(\mathrm{2}{a}−{b}\right)\:\:,\:{y}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{2}{a}−{b}+{p}={r}\:\:\:\:....\left({i}\right) \\ $$$${let}\:\left({s},{t}\right)\:{be}\:{point}\:{of}\:{tangency} \\ $$$${of}\:{red}\:{ellipse}\:{and}\:{circle}. \\ $$$$\left({s}−{p}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \left(\mathrm{1}−\frac{{s}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)={r}^{\mathrm{2}} \\ $$$$\left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\mathrm{1}\right){s}^{\mathrm{2}} +\mathrm{2}{ps}+{r}^{\mathrm{2}} −{p}^{\mathrm{2}} −{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${D}=\mathrm{0} \\ $$$$\Rightarrow\:\:{p}^{\mathrm{2}} =\left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\mathrm{1}\right)\left({r}^{\mathrm{2}} −{p}^{\mathrm{2}} −{a}^{\mathrm{2}} \right) \\ $$$${and}\:{as}\:\:\:{p}={b}+{r}−\mathrm{2}{a} \\ $$$$\left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\mathrm{1}\right){r}^{\mathrm{2}} −{p}^{\mathrm{2}} \left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)={a}^{\mathrm{2}} \left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\mathrm{1}\right) \\ $$$$\left(\mu^{\mathrm{2}} −\mathrm{1}\right){r}^{\mathrm{2}} −\mu^{\mathrm{2}} \left({b}+{r}−\mathrm{2}{a}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={a}^{\mathrm{2}} \left(\mu^{\mathrm{2}} −\mathrm{1}\right) \\ $$$${r}^{\mathrm{2}} −\mathrm{4}\mu^{\mathrm{2}} \left({a}−\frac{{b}}{\mathrm{2}}\right){r}+{a}^{\mathrm{2}} \left(\mu^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{4}\mu^{\mathrm{2}} \left({a}−\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${let}\:\:\:{r}=\lambda{a} \\ $$$$\lambda^{\mathrm{2}} −\mathrm{4}\mu^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\mu}\right)\lambda+\left(\mu^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{4}\mu^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\mu}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\lambda=\mathrm{2}\mu^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\mu}\right)−\sqrt{\mathrm{4}\mu^{\mathrm{2}} \left(\mu^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\mu}\right)^{\mathrm{2}} −\left(\mu^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$\lambda=\mu\left(\mathrm{2}\mu−\mathrm{1}\right)−\sqrt{\left(\mu^{\mathrm{2}} −\mathrm{1}\right)\left\{\left(\mathrm{2}\mu−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right\}} \\ $$$$\:\:\:\:{with}\:\:\:\mu=\mathrm{1}.\mathrm{8393} \\ $$$$\lambda\approx\:\mathrm{1}.\mathrm{09074} \\ $$
Commented by mr W last updated on 22/Apr/20
$${very}\:{nice}\:{solution}\:{sir}!\:{exact}! \\ $$
Commented by ajfour last updated on 22/Apr/20