Question and Answers Forum

All Questions      Topic List

Probability and Statistics Questions

Previous in All Question      Next in All Question      

Previous in Probability and Statistics      Next in Probability and Statistics      

Question Number 93610 by 675480065 last updated on 14/May/20

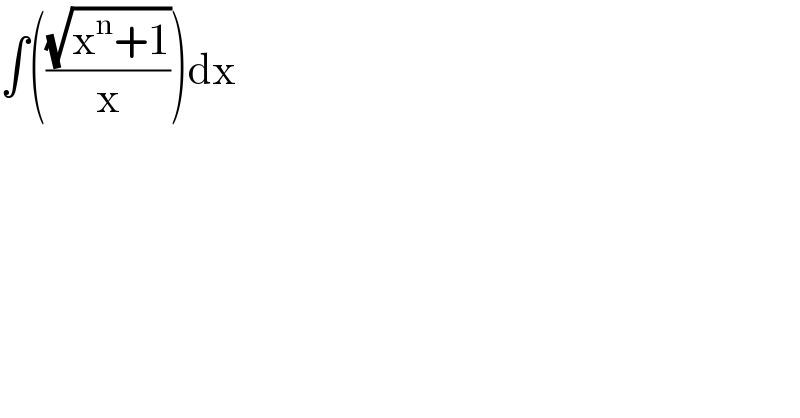
∫(((√(x^n +1))/x))dx

$$\int\left(\frac{\sqrt{\mathrm{x}^{\mathrm{n}} +\mathrm{1}}}{\mathrm{x}}\right)\mathrm{dx} \\ $$

Answered by 1549442205 last updated on 14/May/20

Put 1+x^n =t^n ⇒x^(n−1) dx=t^(n−1) dt.We have F(x)=∫((t^(n/2) ×t^(n−1) )/(t^n −1))dt=∫(t^((n/2)−1) +(t^((n/2)−1) /(t^n −1)))dt =_(t=u^2 ) =((2(√t^n ))/n)+∫(u^(n−2) /(u^(2n) −1))×2udu=((2(√t^n ))/n)+∫((2u^(n−1) )/(u^(2n) −1))du =((2(√t^n ))/n)+(2/n)∫(du^n /(u^(2n) −1))=_(u^n =v) ((2(√t^n ))/n)+(2/n)∫(dv/(v^2 −1)) =((2(√t^n ))/n)+(1/n)∫((1/(v−1))−(1/(v+1)))dv=((2(√(1+x^n )))/n)+ (1/n)ln∣((v−1)/(v+1))∣=((2(√(1+x^n )))/n)+(1/n)ln∣((1−(√(1+x^n )))/(1+(√(1+x^n ))))∣+C

$$\mathrm{Put}\:\mathrm{1}+\mathrm{x}^{\mathrm{n}} =\mathrm{t}^{\mathrm{n}} \Rightarrow\mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{dx}=\mathrm{t}^{\mathrm{n}−\mathrm{1}} \mathrm{dt}.\mathrm{We}\:\mathrm{have} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\int\frac{\mathrm{t}^{\frac{\mathrm{n}}{\mathrm{2}}} ×\mathrm{t}^{\mathrm{n}−\mathrm{1}} }{\mathrm{t}^{\mathrm{n}} −\mathrm{1}}\mathrm{dt}=\int\left(\mathrm{t}^{\frac{\mathrm{n}}{\mathrm{2}}−\mathrm{1}} +\frac{\mathrm{t}^{\frac{\mathrm{n}}{\mathrm{2}}−\mathrm{1}} }{\mathrm{t}^{\mathrm{n}} −\mathrm{1}}\right)\mathrm{dt} \\ $$$$=_{\mathrm{t}=\mathrm{u}^{\mathrm{2}} } =\frac{\mathrm{2}\sqrt{\mathrm{t}^{\mathrm{n}} }}{\mathrm{n}}+\int\frac{\mathrm{u}^{\mathrm{n}−\mathrm{2}} }{\mathrm{u}^{\mathrm{2n}} −\mathrm{1}}×\mathrm{2udu}=\frac{\mathrm{2}\sqrt{\mathrm{t}^{\mathrm{n}} }}{\mathrm{n}}+\int\frac{\mathrm{2u}^{\mathrm{n}−\mathrm{1}} }{\mathrm{u}^{\mathrm{2n}} −\mathrm{1}}\mathrm{du} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{t}^{\mathrm{n}} }}{\mathrm{n}}+\frac{\mathrm{2}}{\mathrm{n}}\int\frac{\mathrm{du}^{\mathrm{n}} }{\mathrm{u}^{\mathrm{2n}} −\mathrm{1}}=_{\mathrm{u}^{\mathrm{n}} =\mathrm{v}} \frac{\mathrm{2}\sqrt{\mathrm{t}^{\mathrm{n}} }}{\mathrm{n}}+\frac{\mathrm{2}}{\mathrm{n}}\int\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{t}^{\mathrm{n}} }}{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{n}}\int\left(\frac{\mathrm{1}}{\mathrm{v}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{v}+\mathrm{1}}\right)\mathrm{dv}=\frac{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{n}} }}{\mathrm{n}}+ \\ $$$$\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\mid\frac{\mathrm{v}−\mathrm{1}}{\mathrm{v}+\mathrm{1}}\mid=\frac{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{n}} }}{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\mid\frac{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{n}} }}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{n}} }}\mid+\mathrm{C} \\ $$

Commented by 675480065 last updated on 14/May/20

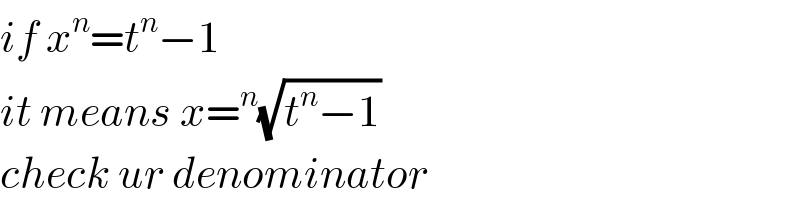
if x^n =t^n −1 it means x=^n (√(t^n −1)) check ur denominator

$${if}\:{x}^{{n}} ={t}^{{n}} −\mathrm{1} \\ $$$${it}\:{means}\:{x}=^{{n}} \sqrt{{t}^{{n}} −\mathrm{1}} \\ $$$${check}\:{ur}\:{denominator} \\ $$

Commented by prakash jain last updated on 14/May/20

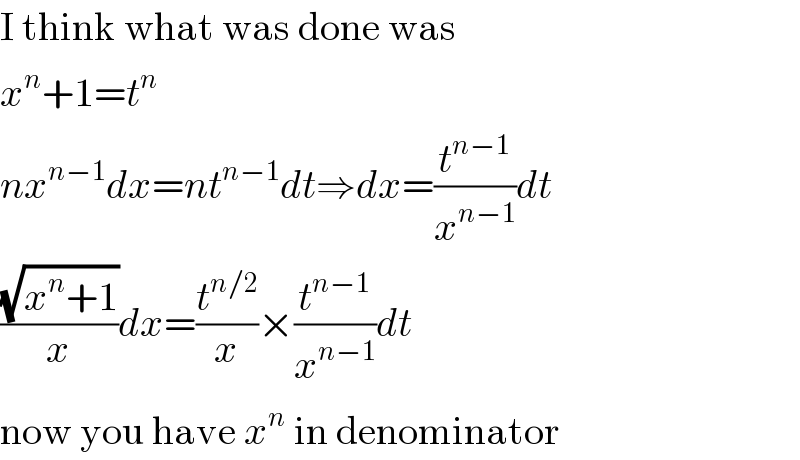
I think what was done was x^n +1=t^n nx^(n−1) dx=nt^(n−1) dt⇒dx=(t^(n−1) /x^(n−1) )dt ((√(x^n +1))/x)dx=(t^(n/2) /x)×(t^(n−1) /x^(n−1) )dt now you have x^n in denominator

$$\mathrm{I}\:\mathrm{think}\:\mathrm{what}\:\mathrm{was}\:\mathrm{done}\:\mathrm{was} \\ $$$${x}^{{n}} +\mathrm{1}={t}^{{n}} \\ $$$${nx}^{{n}−\mathrm{1}} {dx}={nt}^{{n}−\mathrm{1}} {dt}\Rightarrow{dx}=\frac{{t}^{{n}−\mathrm{1}} }{{x}^{{n}−\mathrm{1}} }{dt} \\ $$$$\frac{\sqrt{{x}^{{n}} +\mathrm{1}}}{{x}}{dx}=\frac{{t}^{{n}/\mathrm{2}} }{{x}}×\frac{{t}^{{n}−\mathrm{1}} }{{x}^{{n}−\mathrm{1}} }{dt} \\ $$$$\mathrm{now}\:\mathrm{you}\:\mathrm{have}\:{x}^{{n}} \:\mathrm{in}\:\mathrm{denominator} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com