Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 96012 by mhmd last updated on 29/May/20

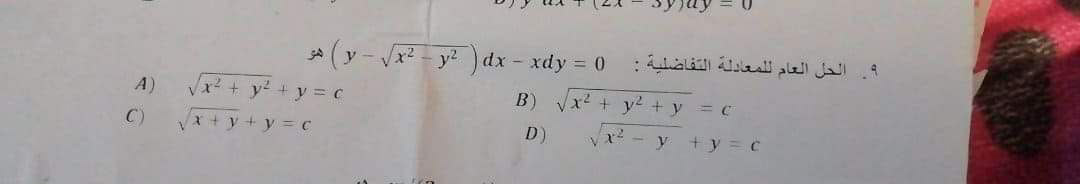
Commented by john santu last updated on 29/May/20

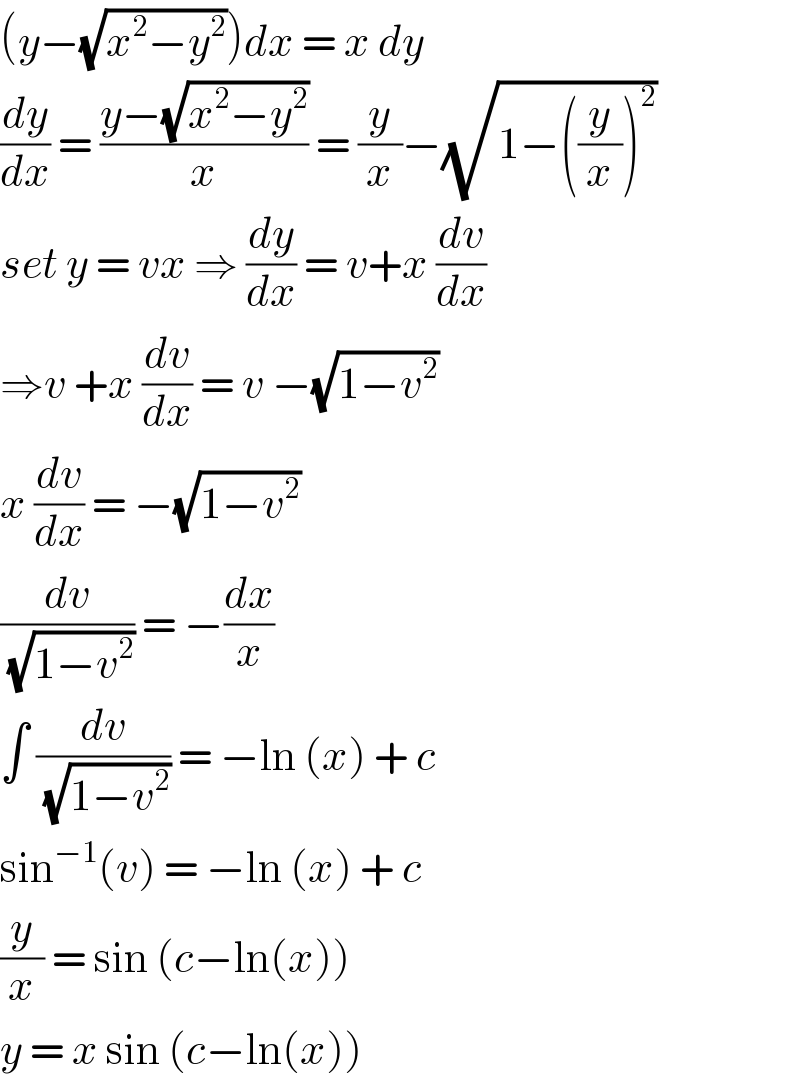
(y−(√(x^2 −y^2 )))dx = x dy (dy/dx) = ((y−(√(x^2 −y^2 )))/x) = (y/x)−(√(1−((y/x))^2 )) set y = vx ⇒ (dy/dx) = v+x (dv/dx) ⇒v +x (dv/dx) = v −(√(1−v^2 )) x (dv/dx) = −(√(1−v^2 )) (dv/(√(1−v^2 ))) = −(dx/x) ∫ (dv/(√(1−v^2 ))) = −ln (x) + c sin^(−1) (v) = −ln (x) + c (y/x) = sin (c−ln(x)) y = x sin (c−ln(x))

$$\left({y}−\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }\right){dx}\:=\:{x}\:{dy}\: \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{{y}−\sqrt{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }}{{x}}\:=\:\frac{{y}}{{x}}−\sqrt{\mathrm{1}−\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} } \\ $$$${set}\:{y}\:=\:{vx}\:\Rightarrow\:\frac{{dy}}{{dx}}\:=\:{v}+{x}\:\frac{{dv}}{{dx}} \\ $$$$\Rightarrow{v}\:+{x}\:\frac{{dv}}{{dx}}\:=\:{v}\:−\sqrt{\mathrm{1}−{v}^{\mathrm{2}} }\: \\ $$$${x}\:\frac{{dv}}{{dx}}\:=\:−\sqrt{\mathrm{1}−{v}^{\mathrm{2}} }\: \\ $$$$\frac{{dv}}{\sqrt{\mathrm{1}−{v}^{\mathrm{2}} }}\:=\:−\frac{{dx}}{{x}}\: \\ $$$$\int\:\frac{{dv}}{\sqrt{\mathrm{1}−{v}^{\mathrm{2}} }}\:=\:−\mathrm{ln}\:\left({x}\right)\:+\:{c}\: \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left({v}\right)\:=\:−\mathrm{ln}\:\left({x}\right)\:+\:{c}\: \\ $$$$\frac{{y}}{{x}}\:=\:\mathrm{sin}\:\left({c}−\mathrm{ln}\left({x}\right)\right)\: \\ $$$${y}\:=\:{x}\:\mathrm{sin}\:\left({c}−\mathrm{ln}\left({x}\right)\right)\: \\ $$

Answered by Sourav mridha last updated on 29/May/20

(y−(√(x^2 −y^2 )))dx−xdy=0 ⇒ydx−xdy=(√(x^2 −y^2 ))dx ⇒−[((xdy−ydx)/x^2 )]=x(√(1−((y/x))^2 )) (dx/x^2 ) integrating both sides−− ⇒−∫[((d((y/x)))/((√(1−((y/x))^2 )) ))] =∫(dx/x) ⇒−sin^(−1) ((y/x))=ln(cx) so,y=−xsin(ln(cx)).

$$\left(\boldsymbol{{y}}−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }\right)\mathrm{dx}−\mathrm{xdy}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{ydx}−\mathrm{xdy}=\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Rightarrow−\left[\frac{\mathrm{xdy}−\mathrm{ydx}}{\mathrm{x}^{\mathrm{2}} }\right]=\mathrm{x}\sqrt{\mathrm{1}−\left(\frac{\mathrm{y}}{\mathrm{x}}\right)^{\mathrm{2}} }\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{integrating}\:\mathrm{both}\:\mathrm{sides}−− \\ $$$$\Rightarrow−\int\left[\frac{\mathrm{d}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)}{\sqrt{\mathrm{1}−\left(\frac{\mathrm{y}}{\mathrm{x}}\right)^{\mathrm{2}} }\:}\right]\:=\int\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$\Rightarrow−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{y}}{\mathrm{x}}\right)=\mathrm{ln}\left(\mathrm{cx}\right) \\ $$$$\mathrm{so},\boldsymbol{{y}}=−\boldsymbol{{xsin}}\left(\boldsymbol{{ln}}\left(\boldsymbol{{cx}}\right)\right). \\ $$

Answered by Sourav mridha last updated on 29/May/20

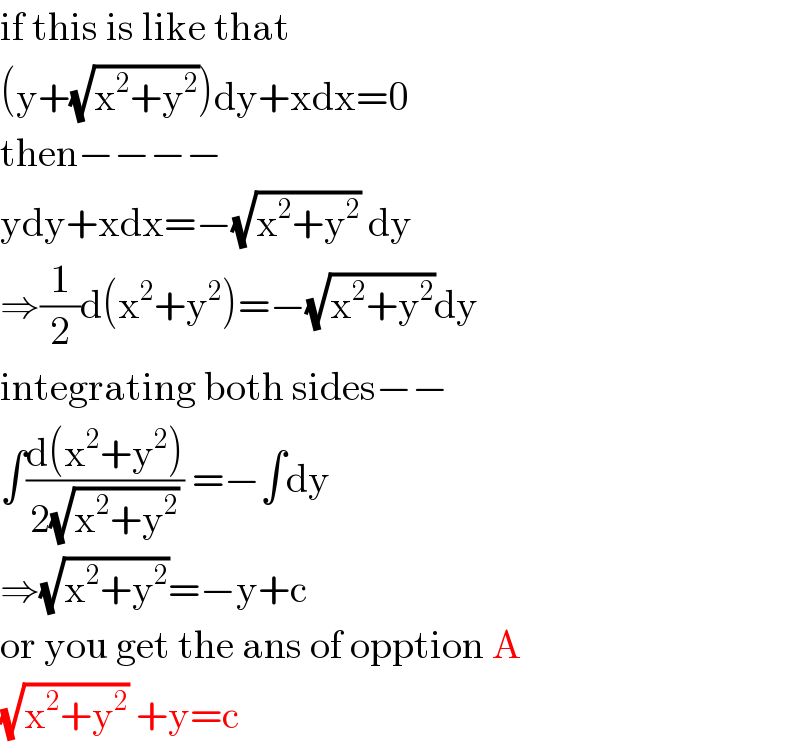
if this is like that (y+(√(x^2 +y^2 )))dy+xdx=0 then−−−− ydy+xdx=−(√(x^2 +y^2 )) dy ⇒(1/2)d(x^2 +y^2 )=−(√(x^2 +y^2 ))dy integrating both sides−− ∫((d(x^2 +y^2 ))/(2(√(x^2 +y^2 )))) =−∫dy ⇒(√(x^2 +y^2 ))=−y+c or you get the ans of opption A (√(x^2 +y^2 )) +y=c

$$\mathrm{if}\:\mathrm{this}\:\mathrm{is}\:\mathrm{like}\:\mathrm{that} \\ $$$$\left(\mathrm{y}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\right)\mathrm{dy}+\mathrm{xdx}=\mathrm{0} \\ $$$$\mathrm{then}−−−− \\ $$$$\mathrm{ydy}+\mathrm{xdx}=−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:\mathrm{dy} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)=−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\mathrm{dy} \\ $$$$\mathrm{integrating}\:\mathrm{both}\:\mathrm{sides}−− \\ $$$$\int\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }}\:=−\int\mathrm{dy} \\ $$$$\Rightarrow\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }=−\mathrm{y}+\mathrm{c} \\ $$$$\mathrm{or}\:\mathrm{you}\:\mathrm{get}\:\mathrm{the}\:\mathrm{ans}\:\mathrm{of}\:\mathrm{opption}\:\mathrm{A} \\ $$$$\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:+\mathrm{y}=\mathrm{c} \\ $$

Commented by mhmd last updated on 29/May/20

very very thank you sir

$${very}\:{very}\:{thank}\:{you}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com