Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 97746 by bemath last updated on 09/Jun/20

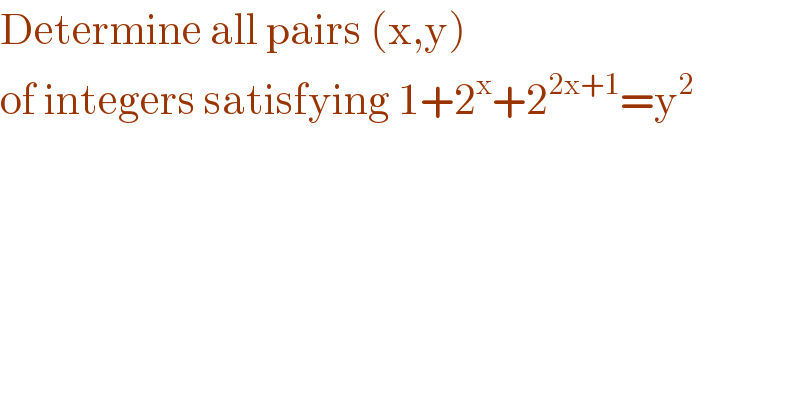
Determine all pairs (x,y) of integers satisfying 1+2^x +2^(2x+1) =y^2

$$\mathrm{Determine}\:\mathrm{all}\:\mathrm{pairs}\:\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\mathrm{of}\:\mathrm{integers}\:\mathrm{satisfying}\:\mathrm{1}+\mathrm{2}^{\mathrm{x}} +\mathrm{2}^{\mathrm{2x}+\mathrm{1}} =\mathrm{y}^{\mathrm{2}} \: \\ $$

Commented by john santu last updated on 09/Jun/20

2^x (1+2^(x+1) ) = (y−1)(y+1) show that the factors y−1 and y+1 are even, exactly one of them divisible by 4. Hence x≥3 and one of these factors is divisible by 2^(x−1) but not by 2^x . so y = 2^(x−1) m+ε , m odd , ε = ±1 plugging this into the original equation we obtain 2^x (1+2^(x+1) )=(2^(x−1) m+ε)^2 −1 = 2^(2x−2) m^2 +2^x mε or equivalently 1+2^(x+1) =2^(x−2) m^2 +mε ⇔ thus we have the complete list solutions (x,y) : (0,2),(0,−2), (4,23),(4,−23).

$$\mathrm{2}^{{x}} \left(\mathrm{1}+\mathrm{2}^{{x}+\mathrm{1}} \right)\:=\:\left({y}−\mathrm{1}\right)\left({y}+\mathrm{1}\right) \\ $$$${show}\:{that}\:{the}\:{factors}\:{y}−\mathrm{1}\:{and}\:{y}+\mathrm{1} \\ $$$${are}\:{even},\:\mathrm{exactly}\:\mathrm{one}\:\mathrm{of}\:\mathrm{them}\: \\ $$$$\mathrm{divisible}\:\mathrm{by}\:\mathrm{4}.\:\mathrm{Hence}\:\mathrm{x}\geqslant\mathrm{3}\:\mathrm{and}\:\mathrm{one} \\ $$$$\mathrm{of}\:\mathrm{these}\:\mathrm{factors}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2}^{\mathrm{x}−\mathrm{1}} \\ $$$$\mathrm{but}\:\mathrm{not}\:\mathrm{by}\:\mathrm{2}^{\mathrm{x}} .\:\mathrm{so}\:\mathrm{y}\:=\:\mathrm{2}^{\mathrm{x}−\mathrm{1}} \mathrm{m}+\epsilon\:,\:\mathrm{m}\:\mathrm{odd}\:,\:\epsilon\:=\:\pm\mathrm{1} \\ $$$$\mathrm{plugging}\:\mathrm{this}\:\mathrm{into}\:\mathrm{the}\:\mathrm{original}\: \\ $$$$\mathrm{equation}\:\mathrm{we}\:\mathrm{obtain}\:\mathrm{2}^{\mathrm{x}} \left(\mathrm{1}+\mathrm{2}^{\mathrm{x}+\mathrm{1}} \right)=\left(\mathrm{2}^{\mathrm{x}−\mathrm{1}} \mathrm{m}+\epsilon\right)^{\mathrm{2}} −\mathrm{1} \\ $$$$=\:\mathrm{2}^{\mathrm{2x}−\mathrm{2}} \mathrm{m}^{\mathrm{2}} +\mathrm{2}^{\mathrm{x}} \mathrm{m}\epsilon \\ $$$$\mathrm{or}\:\mathrm{equivalently}\:\mathrm{1}+\mathrm{2}^{\mathrm{x}+\mathrm{1}} =\mathrm{2}^{\mathrm{x}−\mathrm{2}} \mathrm{m}^{\mathrm{2}} +\mathrm{m}\epsilon \\ $$$$\Leftrightarrow\:\mathrm{thus}\:\mathrm{we}\:\mathrm{have}\:\mathrm{the}\:\mathrm{complete} \\ $$$$\mathrm{list}\:\mathrm{solutions}\:\left(\mathrm{x},\mathrm{y}\right)\::\:\left(\mathrm{0},\mathrm{2}\right),\left(\mathrm{0},−\mathrm{2}\right), \\ $$$$\left(\mathrm{4},\mathrm{23}\right),\left(\mathrm{4},−\mathrm{23}\right).\: \\ $$

Answered by Rasheed.Sindhi last updated on 18/Jun/20

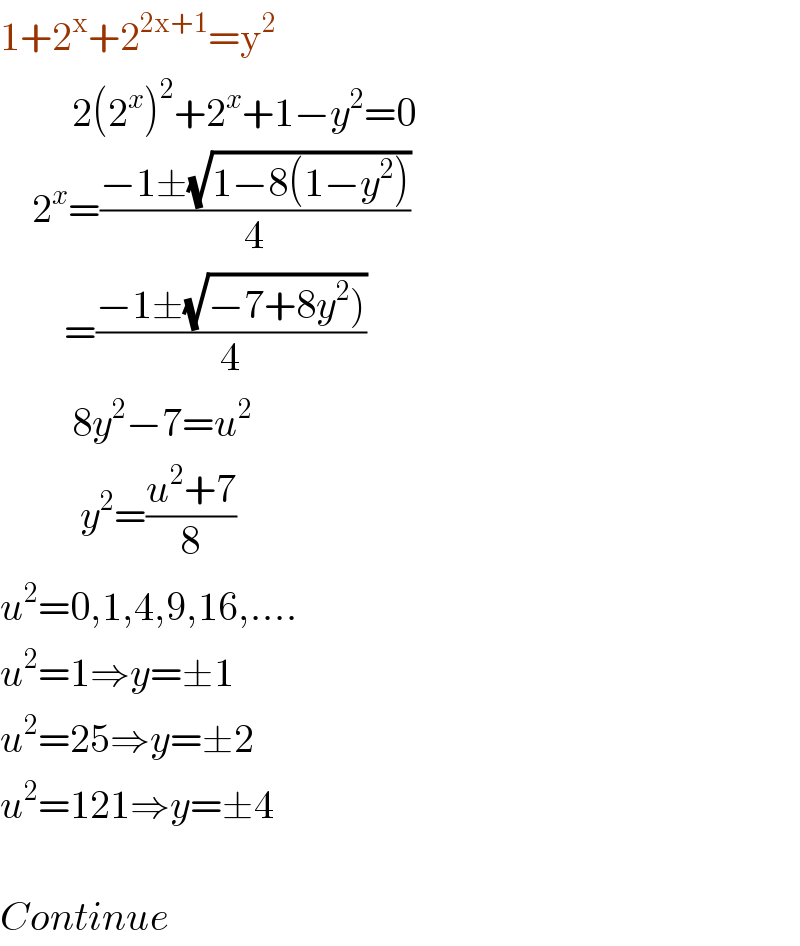
1+2^x +2^(2x+1) =y^2 2(2^x )^2 +2^x +1−y^2 =0 2^x =((−1±(√(1−8(1−y^2 ))))/4) =((−1±(√(−7+8y^2 ))))/4) 8y^2 −7=u^2 y^2 =((u^2 +7)/8) u^2 =0,1,4,9,16,.... u^2 =1⇒y=±1 u^2 =25⇒y=±2 u^2 =121⇒y=±4 Continue

$$\mathrm{1}+\mathrm{2}^{\mathrm{x}} +\mathrm{2}^{\mathrm{2x}+\mathrm{1}} =\mathrm{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{2}\left(\mathrm{2}^{{x}} \right)^{\mathrm{2}} +\mathrm{2}^{{x}} +\mathrm{1}−{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\mathrm{2}^{{x}} =\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{8}\left(\mathrm{1}−{y}^{\mathrm{2}} \right)}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{−\mathrm{1}\pm\sqrt{\left.−\mathrm{7}+\mathrm{8}{y}^{\mathrm{2}} \right)}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{8}{y}^{\mathrm{2}} −\mathrm{7}={u}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{y}^{\mathrm{2}} =\frac{{u}^{\mathrm{2}} +\mathrm{7}}{\mathrm{8}} \\ $$$${u}^{\mathrm{2}} =\mathrm{0},\mathrm{1},\mathrm{4},\mathrm{9},\mathrm{16},.... \\ $$$${u}^{\mathrm{2}} =\mathrm{1}\Rightarrow{y}=\pm\mathrm{1} \\ $$$${u}^{\mathrm{2}} =\mathrm{25}\Rightarrow{y}=\pm\mathrm{2} \\ $$$${u}^{\mathrm{2}} =\mathrm{121}\Rightarrow{y}=\pm\mathrm{4} \\ $$$$ \\ $$$${Continue}\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com