Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 98022 by Ar Brandon last updated on 11/Jun/20

Derive the relation between an Arithmetic Mean and a Geometric Mean ((x_1 x_2 ...x_n ))^(1/n) ≤((x_1 +x_2 +∙∙∙+x_n )/n) ∀n∈N^∗ , ∀(x_1 ,x_2 ,...x_n )∈(R_+ ^∗ )^n

$$\mathcal{D}\mathrm{erive}\:\mathrm{the}\:\mathrm{relation}\:\mathrm{between}\:\mathrm{an}\:\mathcal{A}\mathrm{rithmetic}\:\mathcal{M}\mathrm{ean} \\ $$$$\mathrm{and}\:\mathrm{a}\:\mathcal{G}\mathrm{eometric}\:\mathcal{M}\mathrm{ean} \\ $$$$\sqrt[{\mathrm{n}}]{\mathrm{x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} ...\mathrm{x}_{\mathrm{n}} }\leqslant\frac{\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} +\centerdot\centerdot\centerdot+\mathrm{x}_{\mathrm{n}} }{\mathrm{n}}\:\forall\mathrm{n}\in\mathbb{N}^{\ast} ,\:\forall\left(\mathrm{x}_{\mathrm{1}} ,\mathrm{x}_{\mathrm{2}} ,...\mathrm{x}_{\mathrm{n}} \right)\in\left(\mathbb{R}_{+} ^{\ast} \right)^{\mathrm{n}} \\ $$

Answered by Rio Michael last updated on 11/Jun/20

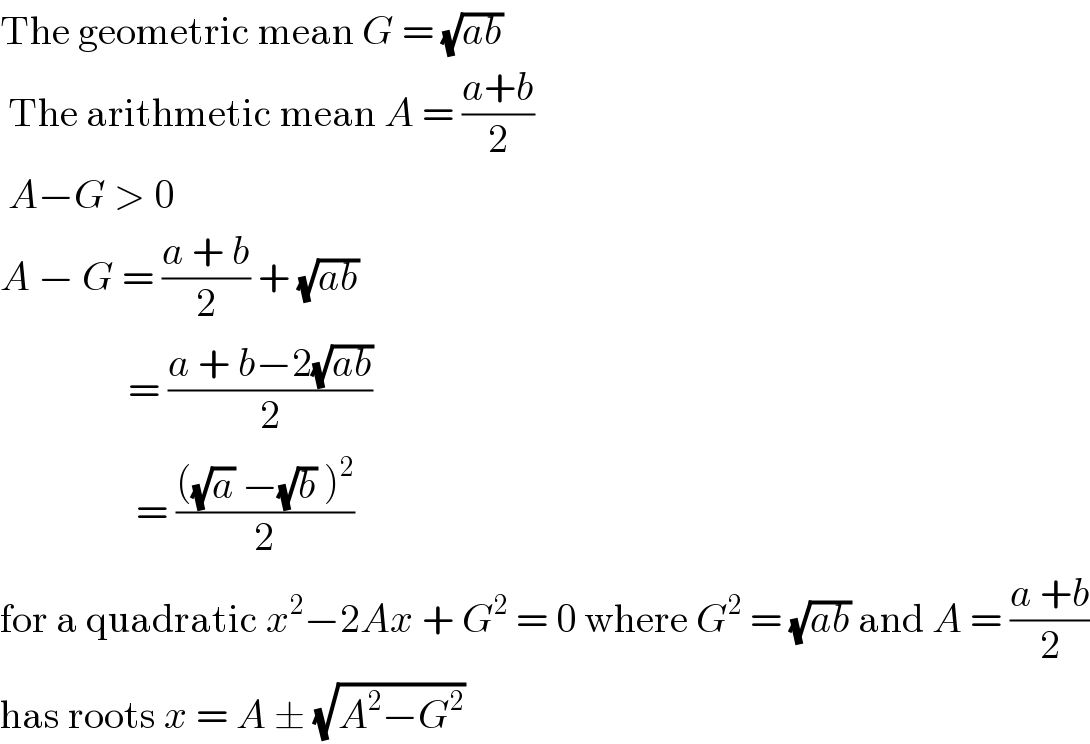
The geometric mean G = (√(ab)) The arithmetic mean A = ((a+b)/2) A−G > 0 A − G = ((a + b)/2) + (√(ab)) = ((a + b−2(√(ab)))/2) = ((((√a) −(√b) )^2 )/2) for a quadratic x^2 −2Ax + G^2 = 0 where G^2 = (√(ab)) and A = ((a +b)/2) has roots x = A ± (√(A^2 −G^2 ))

$$\mathrm{The}\:\mathrm{geometric}\:\mathrm{mean}\:{G}\:=\:\sqrt{{ab}}\: \\ $$$$\:\mathrm{The}\:\mathrm{arithmetic}\:\mathrm{mean}\:{A}\:=\:\frac{{a}+{b}}{\mathrm{2}} \\ $$$$\:{A}−{G}\:>\:\mathrm{0}\: \\ $$$${A}\:−\:{G}\:=\:\frac{{a}\:+\:{b}}{\mathrm{2}}\:+\:\sqrt{{ab}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{a}\:+\:{b}−\mathrm{2}\sqrt{{ab}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\left(\sqrt{{a}}\:−\sqrt{{b}}\:\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{for}\:\mathrm{a}\:\mathrm{quadratic}\:{x}^{\mathrm{2}} −\mathrm{2}{Ax}\:+\:{G}^{\mathrm{2}} \:=\:\mathrm{0}\:\mathrm{where}\:{G}^{\mathrm{2}} \:=\:\sqrt{{ab}}\:\mathrm{and}\:{A}\:=\:\frac{{a}\:+{b}}{\mathrm{2}} \\ $$$$\mathrm{has}\:\mathrm{roots}\:{x}\:=\:{A}\:\pm\:\sqrt{{A}^{\mathrm{2}} −{G}^{\mathrm{2}} } \\ $$

Commented by Ar Brandon last updated on 11/Jun/20

Thanks for your time. But actually, the question requires us to derive the above relation, instead of solving for x.

$$\mathcal{T}\mathrm{hanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}.\:\mathcal{B}\mathrm{ut}\:\mathrm{actually},\:\mathrm{the}\:\mathrm{question}\:\mathrm{requires} \\ $$$$\mathrm{us}\:\mathrm{to}\:\mathrm{derive}\:\mathrm{the}\:\mathrm{above}\:\mathrm{relation},\:\mathrm{instead}\:\mathrm{of}\:\mathrm{solving}\:\mathrm{for}\:\mathrm{x}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com