Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 98942 by mathmax by abdo last updated on 17/Jun/20

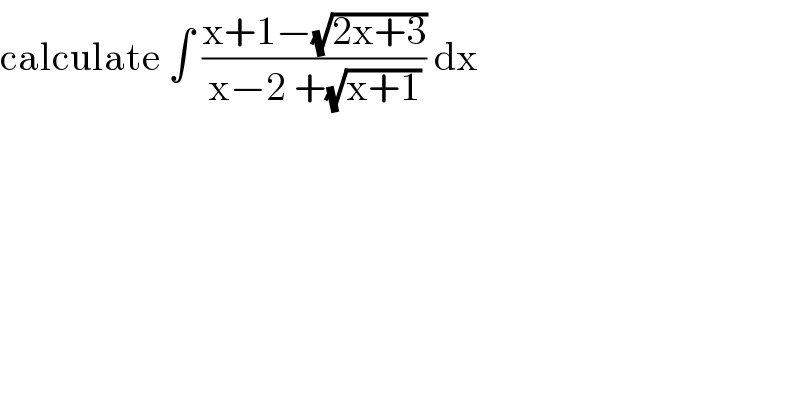
calculate ∫ ((x+1−(√(2x+3)))/(x−2 +(√(x+1)))) dx

$$\mathrm{calculate}\:\int\:\frac{\mathrm{x}+\mathrm{1}−\sqrt{\mathrm{2x}+\mathrm{3}}}{\mathrm{x}−\mathrm{2}\:+\sqrt{\mathrm{x}+\mathrm{1}}}\:\mathrm{dx} \\ $$

Commented by MJS last updated on 17/Jun/20

Sir Abdo, do you have an easy solution? I can solve it but the constants are getting horrible...

$$\mathrm{Sir}\:\mathrm{Abdo},\:\mathrm{do}\:\mathrm{you}\:\mathrm{have}\:\mathrm{an}\:\mathrm{easy}\:\mathrm{solution}? \\ $$$$\mathrm{I}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{but}\:\mathrm{the}\:\mathrm{constants}\:\mathrm{are}\:\mathrm{getting} \\ $$$$\mathrm{horrible}... \\ $$

Commented by mathmax by abdo last updated on 18/Jun/20

use hyperbolic function sir.

$$\mathrm{use}\:\mathrm{hyperbolic}\:\mathrm{function}\:\mathrm{sir}. \\ $$

Answered by 4635 last updated on 17/Jun/20

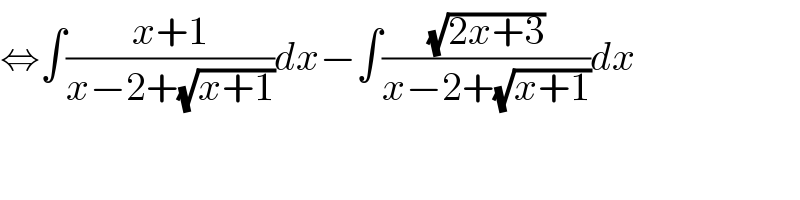
⇔∫((x+1)/(x−2+(√(x+1))))dx−∫((√(2x+3))/(x−2+(√(x+1))))dx

$$\Leftrightarrow\int\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}+\sqrt{{x}+\mathrm{1}}}{dx}−\int\frac{\sqrt{\mathrm{2}{x}+\mathrm{3}}}{{x}−\mathrm{2}+\sqrt{{x}+\mathrm{1}}}{dx} \\ $$

Commented by 4635 last updated on 17/Jun/20

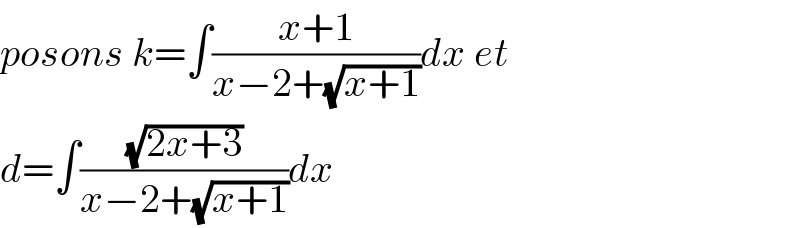
posons k=∫((x+1)/(x−2+(√(x+1))))dx et d=∫((√(2x+3))/(x−2+(√(x+1))))dx

$${posons}\:{k}=\int\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}+\sqrt{{x}+\mathrm{1}}}{dx}\:{et} \\ $$$${d}=\int\frac{\sqrt{\mathrm{2}{x}+\mathrm{3}}}{{x}−\mathrm{2}+\sqrt{{x}+\mathrm{1}}}{dx} \\ $$

Commented by 4635 last updated on 17/Jun/20

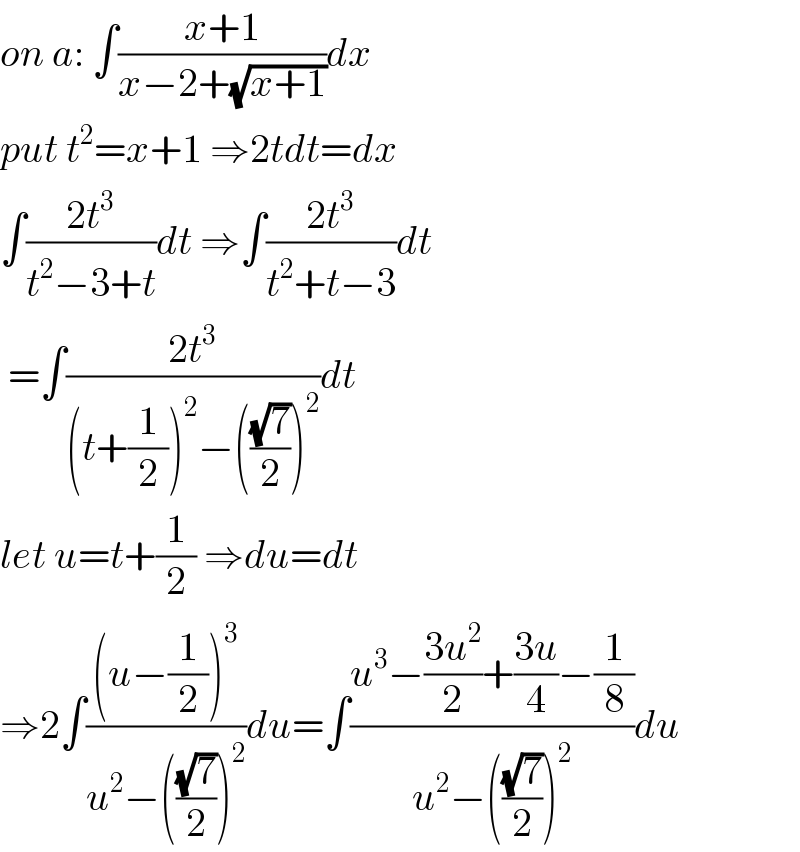
on a: ∫((x+1)/(x−2+(√(x+1))))dx put t^2 =x+1 ⇒2tdt=dx ∫((2t^3 )/(t^2 −3+t))dt ⇒∫((2t^3 )/(t^2 +t−3))dt =∫((2t^3 )/((t+(1/2))^2 −(((√7)/2))^2 ))dt let u=t+(1/2) ⇒du=dt ⇒2∫(((u−(1/2))^3 )/(u^2 −(((√7)/2))^2 ))du=∫((u^3 −((3u^2 )/2)+((3u)/4)−(1/8))/(u^2 −(((√7)/2))^2 ))du

$${on}\:{a}:\:\int\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}+\sqrt{{x}+\mathrm{1}}}{dx} \\ $$$${put}\:{t}^{\mathrm{2}} ={x}+\mathrm{1}\:\Rightarrow\mathrm{2}{tdt}={dx} \\ $$$$\int\frac{\mathrm{2}{t}^{\mathrm{3}} }{{t}^{\mathrm{2}} −\mathrm{3}+{t}}{dt}\:\Rightarrow\int\frac{\mathrm{2}{t}^{\mathrm{3}} }{{t}^{\mathrm{2}} +{t}−\mathrm{3}}{dt} \\ $$$$\:=\int\frac{\mathrm{2}{t}^{\mathrm{3}} }{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right)^{\mathrm{2}} }{dt} \\ $$$${let}\:{u}={t}+\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{du}={dt} \\ $$$$\Rightarrow\mathrm{2}\int\frac{\left({u}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} }{{u}^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right)^{\mathrm{2}} }{du}=\int\frac{{u}^{\mathrm{3}} −\frac{\mathrm{3}{u}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}{u}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}}}{{u}^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right)^{\mathrm{2}} }{du} \\ $$

Answered by MJS last updated on 17/Jun/20

∫((x+1−(√(2x+3)))/(x−2+(√(x+1))))dx= =∫((x+1)/(x−2+(√(x+1))))dx−∫((√(2x+3))/(x−2+(√(x+1))))dx ∫((x+1)/(x−2+(√(x+1))))dx= [t=(√(x+1)) → dx=2(√(x+1))dt] =2∫(t^3 /(t^2 +t−3))dt=2(∫tdt−∫dt+∫((4t−3)/(t^2 +t−3))dt)= =t(t−2)+(4/(13))((26+5(√(13)))∫(dt/(2t+1+(√(13))))+(26−5(√(13)))∫(dt/(2t+1−(√(13))))) and these are easy to solve −∫((√(2x+3))/(x−2+(√(x+1))))dx=−∫(((x−2−(√(x+1)))(√(2x+3)))/(x^2 −5x+3))dx= =−∫(((x−2)(√(2x+3)))/(x^2 −5x+3))dx+∫(((√(x+1))(√(2x+3)))/(x^2 −5x+3))dx −∫(((x−2)(√(2x+3)))/(x^2 −5x+3))dx= [u=(√(2x+3)) → dx=(√(2x+3))du] =−2∫((u^2 (u^2 −7))/(u^4 −16u^2 +51))du u^4 −16u^2 +51=(u−α)(u+α)(u−β)(u+β) α, β ∈R ⇒ we can easily solve this by decomposing ∫(((√(x+1))(√(2x+3)))/(x^2 −5x+3))dx= [v=((√(2(x+1)))/(√(2x+3))) → dx=(√(2(x+1)(2x+3)^3 ))dv] =2(√2)∫(v^2 /((v^2 −1)(51v^4 −86v^2 +36)))dv 51v^4 −86v^2 +36=51(v−γ)(v+γ)(v−δ)(v+γ) γ, δ ∈R ⇒ again easy to solve ...but I′m not eager for typing the constants...

$$\int\frac{{x}+\mathrm{1}−\sqrt{\mathrm{2}{x}+\mathrm{3}}}{{x}−\mathrm{2}+\sqrt{{x}+\mathrm{1}}}{dx}= \\ $$$$=\int\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}+\sqrt{{x}+\mathrm{1}}}{dx}−\int\frac{\sqrt{\mathrm{2}{x}+\mathrm{3}}}{{x}−\mathrm{2}+\sqrt{{x}+\mathrm{1}}}{dx} \\ $$$$\int\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}+\sqrt{{x}+\mathrm{1}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}+\mathrm{1}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}+\mathrm{1}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{3}} }{{t}^{\mathrm{2}} +{t}−\mathrm{3}}{dt}=\mathrm{2}\left(\int{tdt}−\int{dt}+\int\frac{\mathrm{4}{t}−\mathrm{3}}{{t}^{\mathrm{2}} +{t}−\mathrm{3}}{dt}\right)= \\ $$$$={t}\left({t}−\mathrm{2}\right)+\frac{\mathrm{4}}{\mathrm{13}}\left(\left(\mathrm{26}+\mathrm{5}\sqrt{\mathrm{13}}\right)\int\frac{{dt}}{\mathrm{2}{t}+\mathrm{1}+\sqrt{\mathrm{13}}}+\left(\mathrm{26}−\mathrm{5}\sqrt{\mathrm{13}}\right)\int\frac{{dt}}{\mathrm{2}{t}+\mathrm{1}−\sqrt{\mathrm{13}}}\right) \\ $$$$\mathrm{and}\:\mathrm{these}\:\mathrm{are}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$$$−\int\frac{\sqrt{\mathrm{2}{x}+\mathrm{3}}}{{x}−\mathrm{2}+\sqrt{{x}+\mathrm{1}}}{dx}=−\int\frac{\left({x}−\mathrm{2}−\sqrt{{x}+\mathrm{1}}\right)\sqrt{\mathrm{2}{x}+\mathrm{3}}}{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}}{dx}= \\ $$$$=−\int\frac{\left({x}−\mathrm{2}\right)\sqrt{\mathrm{2}{x}+\mathrm{3}}}{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}}{dx}+\int\frac{\sqrt{{x}+\mathrm{1}}\sqrt{\mathrm{2}{x}+\mathrm{3}}}{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}}{dx} \\ $$$$−\int\frac{\left({x}−\mathrm{2}\right)\sqrt{\mathrm{2}{x}+\mathrm{3}}}{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}}{dx}= \\ $$$$\:\:\:\:\:\left[{u}=\sqrt{\mathrm{2}{x}+\mathrm{3}}\:\rightarrow\:{dx}=\sqrt{\mathrm{2}{x}+\mathrm{3}}{du}\right] \\ $$$$=−\mathrm{2}\int\frac{{u}^{\mathrm{2}} \left({u}^{\mathrm{2}} −\mathrm{7}\right)}{{u}^{\mathrm{4}} −\mathrm{16}{u}^{\mathrm{2}} +\mathrm{51}}{du} \\ $$$$\:\:\:\:\:{u}^{\mathrm{4}} −\mathrm{16}{u}^{\mathrm{2}} +\mathrm{51}=\left({u}−\alpha\right)\left({u}+\alpha\right)\left({u}−\beta\right)\left({u}+\beta\right) \\ $$$$\:\:\:\:\:\alpha,\:\beta\:\in\mathbb{R} \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{we}\:\mathrm{can}\:\mathrm{easily}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{by}\:\mathrm{decomposing} \\ $$$$\int\frac{\sqrt{{x}+\mathrm{1}}\sqrt{\mathrm{2}{x}+\mathrm{3}}}{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}}{dx}= \\ $$$$\:\:\:\:\:\left[{v}=\frac{\sqrt{\mathrm{2}\left({x}+\mathrm{1}\right)}}{\sqrt{\mathrm{2}{x}+\mathrm{3}}}\:\rightarrow\:{dx}=\sqrt{\mathrm{2}\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{3}} }{dv}\right] \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\int\frac{{v}^{\mathrm{2}} }{\left({v}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{51}{v}^{\mathrm{4}} −\mathrm{86}{v}^{\mathrm{2}} +\mathrm{36}\right)}{dv} \\ $$$$\:\:\:\:\:\mathrm{51}{v}^{\mathrm{4}} −\mathrm{86}{v}^{\mathrm{2}} +\mathrm{36}=\mathrm{51}\left({v}−\gamma\right)\left({v}+\gamma\right)\left({v}−\delta\right)\left({v}+\gamma\right) \\ $$$$\:\:\:\:\:\gamma,\:\delta\:\in\mathbb{R} \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{again}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$$$...\mathrm{but}\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{eager}\:\mathrm{for}\:\mathrm{typing}\:\mathrm{the}\:\mathrm{constants}... \\ $$

Commented by mathmax by abdo last updated on 18/Jun/20

thank you sir mjs.

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{mjs}. \\ $$

Answered by mathmax by abdo last updated on 18/Jun/20

I =∫ ((x+1−(√(2x+3)))/(x−2+(√(x+1)))) dx ⇒ I =∫ ((x+1)/(x−2+(√(x+1))))dx −∫ ((√(2x+3))/(x−2+(√(x+1))))dx =H−K changement (√(x+1))=t give x+1 =t^2 ⇒ H =∫ (t^2 /(t^2 −1−2+t))(2t)dt = 2 ∫ (t^3 /(t^2 +t−3))dt =2 ∫ ((t(t^2 +t−3)−t^2 +3t)/(t^2 +t−3))dt = 2 ∫ tdt +2 ∫ ((−t^2 +3t)/(t^2 +t−3))dt =t^2 −2 ∫ ((t^2 −3t)/(t^2 +t−3))dt =t^2 −2 ∫ ((t^2 +t−3 −t+3−3t)/(t^2 +t−3))dt =t^2 −2t +2∫ ((4t−3)/(t^2 +t−3))dt t^2 +t−3 =0→Δ =1+12 =13 ⇒t_1 =((−1+(√(13)))/2) and t_2 =((−1−(√(13)))/2) f(t) =((4t−3)/(t^2 +t−3)) =((4t−3)/((t−t_1 )(t−t_2 ))) =(a/(t−t_1 )) +(b/(t−t_2 )) ⇒eazy to find a and b ⇒ ∫ f(t)dt =aln∣t−t_1 ∣ +bln∣t−t_2 ∣ +c ⇒ H =x+1−2(√(x+1)) +2aln∣(√(x+1))−t_1 ∣ +2b ln∣(√(x+1))−t_2 ∣ +c K =∫ ((√(2x+3))/(x−2+(√(x+1))))dt changement (√(x+1))=t give x+1 =t^2 K =∫ ((√(2(t^2 −1)+3))/(t^2 −1−2 +t))(2t)dt =2 ∫ ((√(2t^2 +1))/(t^2 +t−3))tdt =2 ∫ ((t(√(2(t^2 +(1/2)))))/(t^2 +t−3))dt =2(√2) ∫ ((t(√(t^2 +(1/2))))/(t^2 +t−3))dt we do the changement t =(1/(√2))shu ⇒ K =(√2) ∫ ((shu×chu)/((1/2)sh^2 u +(1/(√2))shu −3))((1/(√2)))chu du =∫ ((2shu ch^2 u)/(sh^2 u +(√2)shu −6)) du this integrale is solvable ...be continued...

$$\mathrm{I}\:=\int\:\:\frac{\mathrm{x}+\mathrm{1}−\sqrt{\mathrm{2x}+\mathrm{3}}}{\mathrm{x}−\mathrm{2}+\sqrt{\mathrm{x}+\mathrm{1}}}\:\mathrm{dx}\:\Rightarrow\:\mathrm{I}\:=\int\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{2}+\sqrt{\mathrm{x}+\mathrm{1}}}\mathrm{dx}\:−\int\:\frac{\sqrt{\mathrm{2x}+\mathrm{3}}}{\mathrm{x}−\mathrm{2}+\sqrt{\mathrm{x}+\mathrm{1}}}\mathrm{dx}\:=\mathrm{H}−\mathrm{K} \\ $$$$\mathrm{changement}\:\sqrt{\mathrm{x}+\mathrm{1}}=\mathrm{t}\:\mathrm{give}\:\mathrm{x}+\mathrm{1}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{H}\:=\int\:\:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{1}−\mathrm{2}+\mathrm{t}}\left(\mathrm{2t}\right)\mathrm{dt}\:=\:\mathrm{2}\:\int\:\:\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}−\mathrm{3}}\mathrm{dt} \\ $$$$=\mathrm{2}\:\int\:\frac{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{t}−\mathrm{3}\right)−\mathrm{t}^{\mathrm{2}} +\mathrm{3t}}{\mathrm{t}^{\mathrm{2}} +\mathrm{t}−\mathrm{3}}\mathrm{dt}\:=\:\mathrm{2}\:\int\:\mathrm{tdt}\:+\mathrm{2}\:\int\:\frac{−\mathrm{t}^{\mathrm{2}} \:+\mathrm{3t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}−\mathrm{3}}\mathrm{dt} \\ $$$$=\mathrm{t}^{\mathrm{2}} \:−\mathrm{2}\:\int\:\:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{3t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}−\mathrm{3}}\mathrm{dt}\:\:=\mathrm{t}^{\mathrm{2}} −\mathrm{2}\:\int\:\frac{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}−\mathrm{3}\:−\mathrm{t}+\mathrm{3}−\mathrm{3t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}−\mathrm{3}}\mathrm{dt}\:=\mathrm{t}^{\mathrm{2}} −\mathrm{2t}\:+\mathrm{2}\int\:\frac{\mathrm{4t}−\mathrm{3}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}−\mathrm{3}}\mathrm{dt} \\ $$$$\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}−\mathrm{3}\:=\mathrm{0}\rightarrow\Delta\:=\mathrm{1}+\mathrm{12}\:=\mathrm{13}\:\Rightarrow\mathrm{t}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{13}}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$$\mathrm{f}\left(\mathrm{t}\right)\:=\frac{\mathrm{4t}−\mathrm{3}}{\mathrm{t}^{\mathrm{2}} +\mathrm{t}−\mathrm{3}}\:=\frac{\mathrm{4t}−\mathrm{3}}{\left(\mathrm{t}−\mathrm{t}_{\mathrm{1}} \right)\left(\mathrm{t}−\mathrm{t}_{\mathrm{2}} \right)}\:=\frac{\mathrm{a}}{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }\:+\frac{\mathrm{b}}{\mathrm{t}−\mathrm{t}_{\mathrm{2}} }\:\Rightarrow\mathrm{eazy}\:\mathrm{to}\:\mathrm{find}\:\mathrm{a}\:\mathrm{and}\:\mathrm{b}\:\Rightarrow \\ $$$$\int\:\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{aln}\mid\mathrm{t}−\mathrm{t}_{\mathrm{1}} \mid\:+\mathrm{bln}\mid\mathrm{t}−\mathrm{t}_{\mathrm{2}} \mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{H}\:=\mathrm{x}+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{x}+\mathrm{1}}\:+\mathrm{2aln}\mid\sqrt{\mathrm{x}+\mathrm{1}}−\mathrm{t}_{\mathrm{1}} \mid\:+\mathrm{2b}\:\mathrm{ln}\mid\sqrt{\mathrm{x}+\mathrm{1}}−\mathrm{t}_{\mathrm{2}} \mid\:+\mathrm{c} \\ $$$$\mathrm{K}\:=\int\:\:\frac{\sqrt{\mathrm{2x}+\mathrm{3}}}{\mathrm{x}−\mathrm{2}+\sqrt{\mathrm{x}+\mathrm{1}}}\mathrm{dt}\:\:\mathrm{changement}\:\:\sqrt{\mathrm{x}+\mathrm{1}}=\mathrm{t}\:\mathrm{give}\:\mathrm{x}+\mathrm{1}\:=\mathrm{t}^{\mathrm{2}} \\ $$$$\mathrm{K}\:=\int\:\:\frac{\sqrt{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{3}}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}−\mathrm{2}\:+\mathrm{t}}\left(\mathrm{2t}\right)\mathrm{dt}\:=\mathrm{2}\:\int\:\:\frac{\sqrt{\mathrm{2t}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}−\mathrm{3}}\mathrm{tdt} \\ $$$$=\mathrm{2}\:\int\:\:\frac{\mathrm{t}\sqrt{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}\right)}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}−\mathrm{3}}\mathrm{dt}\:=\mathrm{2}\sqrt{\mathrm{2}}\:\int\:\:\frac{\mathrm{t}\sqrt{\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}−\mathrm{3}}\mathrm{dt}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\: \\ $$$$\mathrm{t}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\mathrm{shu}\:\Rightarrow\:\mathrm{K}\:=\sqrt{\mathrm{2}}\:\int\:\:\:\:\frac{\mathrm{shu}×\mathrm{chu}}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sh}^{\mathrm{2}} \mathrm{u}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\mathrm{shu}\:−\mathrm{3}}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)\mathrm{chu}\:\mathrm{du} \\ $$$$=\int\:\:\frac{\mathrm{2shu}\:\mathrm{ch}^{\mathrm{2}} \mathrm{u}}{\mathrm{sh}^{\mathrm{2}} \mathrm{u}\:+\sqrt{\mathrm{2}}\mathrm{shu}\:−\mathrm{6}}\:\mathrm{du}\:\:\:\mathrm{this}\:\mathrm{integrale}\:\mathrm{is}\:\mathrm{solvable}\:...\mathrm{be}\:\mathrm{continued}... \\ $$

Commented by MJS last updated on 18/Jun/20

this leads to a polynome of 4^(th) degree in the denominator, too. we can solve it but the constants are horrible also

$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{4}^{\mathrm{th}} \:\mathrm{degree}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{denominator},\:\mathrm{too}.\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{but}\:\mathrm{the} \\ $$$$\mathrm{constants}\:\mathrm{are}\:\mathrm{horrible}\:\mathrm{also} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com