Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 99853 by Dwaipayan Shikari last updated on 23/Jun/20

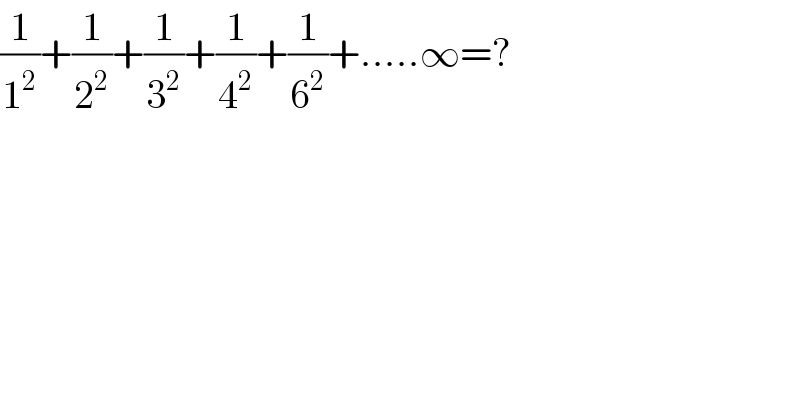
(1/1^2 )+(1/2^2 )+(1/3^2 )+(1/4^2 )+(1/6^2 )+.....∞=?

$$\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{2}} }+.....\infty=? \\ $$

Answered by smridha last updated on 23/Jun/20

Σ_(n=1) ^∞ n^(−2) =𝛇(2)=(𝛑^2 /6)

$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{−\mathrm{2}} =\boldsymbol{\zeta}\left(\mathrm{2}\right)=\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{6}} \\ $$

Commented by Dwaipayan Shikari last updated on 23/Jun/20

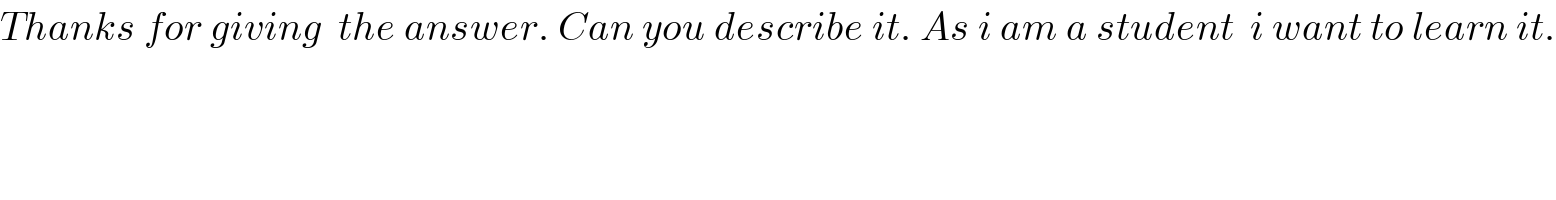
Thanks for giving the answer. Can you describe it. As i am a student i want to learn it.

$${Thanks}\:{for}\:{giving}\:\:{the}\:{answer}.\:{Can}\:{you}\:{describe}\:{it}.\:{As}\:{i}\:{am}\:{a}\:{student}\:\:{i}\:{want}\:{to}\:{learn}\:{it}. \\ $$

Commented by abdomathmax last updated on 23/Jun/20

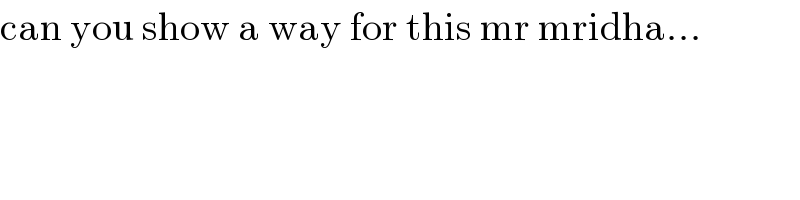
can you show a way for this mr mridha...

$$\mathrm{can}\:\mathrm{you}\:\mathrm{show}\:\mathrm{a}\:\mathrm{way}\:\mathrm{for}\:\mathrm{this}\:\mathrm{mr}\:\mathrm{mridha}... \\ $$

Commented by smridha last updated on 23/Jun/20

okkk i can

$$\boldsymbol{{okkk}}\:\boldsymbol{{i}}\:\boldsymbol{{can}} \\ $$

Commented by smridha last updated on 23/Jun/20

B_(2n) =(−1)^(n−1) ((2(2n)!)/((2𝛑)^(2n) ))𝛇(2n) this is the relation bet^n Bernoulli number and Reimann zeta f^n now put n=1 you get.. B_2 =(−1)^(1−1) ((2.2!)/((2𝛑)^2 ))𝛇(2) we know B_2 =(1/6) putting it you get 𝛇(2)=(𝛑^2 /6).

$$\boldsymbol{{B}}_{\mathrm{2}\boldsymbol{{n}}} =\left(−\mathrm{1}\right)^{\boldsymbol{{n}}−\mathrm{1}} \frac{\mathrm{2}\left(\mathrm{2}\boldsymbol{{n}}\right)!}{\left(\mathrm{2}\boldsymbol{\pi}\right)^{\mathrm{2}{n}} }\boldsymbol{\zeta}\left(\mathrm{2}{n}\right) \\ $$$$\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{the}}\:\boldsymbol{{relation}}\:\boldsymbol{{bet}}^{\boldsymbol{{n}}} \:\boldsymbol{{Bernoulli}} \\ $$$$\boldsymbol{{number}}\:\boldsymbol{{and}}\:\boldsymbol{{Reimann}}\:\boldsymbol{{zeta}}\:\boldsymbol{{f}}^{\boldsymbol{{n}}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{put}}\:\boldsymbol{{n}}=\mathrm{1}\:\boldsymbol{{you}}\:\boldsymbol{{get}}.. \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{B}}_{\mathrm{2}} =\left(−\mathrm{1}\right)^{\mathrm{1}−\mathrm{1}} \frac{\mathrm{2}.\mathrm{2}!}{\left(\mathrm{2}\boldsymbol{\pi}\right)^{\mathrm{2}} }\boldsymbol{\zeta}\left(\mathrm{2}\right) \\ $$$$\boldsymbol{{we}}\:\boldsymbol{{know}}\:\boldsymbol{{B}}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}}\:\boldsymbol{{putting}}\:\boldsymbol{{it}}\:\boldsymbol{{you}}\:\boldsymbol{{get}} \\ $$$$\:\:\:\:\:\:\boldsymbol{\zeta}\left(\mathrm{2}\right)=\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{6}}. \\ $$

Commented by smridha last updated on 23/Jun/20

another way: sinx=xΠ_(n=1) ^∞ (1−(x^2 /(n^2 𝛑^2 ))) ⇒((sin(x))/x)=(1−(x^2 /(1^2 𝛑^2 )))(1−(x^2 /(2^2 𝛑^2 )))(1−(x^2 /(3^2 𝛑^2 )))........ .............................. (i) we know:sinx=x−(x^3 /(3!))+(x^5 /(5!))−...... so ((sin(x))/x)=1−(x^2 /(3!))+(x^4 /(5!))−........ now compare the x^2 terms both sides of the eq^n (i) we will get (1/(1^2 𝛑^2 ))+(1/(2^2 𝛑^2 ))+(1/(3^2 𝛑^2 ))+.....=(1/(3!)) so finally we get: (1/1^2 )+(1/2^2 )+(1/3^2 )+(1/4^2 )+....∞=𝛇(2)=(𝛑^2 /6).

$$\boldsymbol{{another}}\:\boldsymbol{{way}}: \\ $$$$\boldsymbol{{sinx}}=\boldsymbol{{x}}\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\boldsymbol{{n}}^{\mathrm{2}} \boldsymbol{\pi}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}=\left(\mathrm{1}−\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{1}^{\mathrm{2}} \boldsymbol{\pi}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} \boldsymbol{\pi}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} \boldsymbol{\pi}^{\mathrm{2}} }\right)........ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:..............................\:\left(\boldsymbol{{i}}\right) \\ $$$$\boldsymbol{{we}}\:\boldsymbol{{know}}:\boldsymbol{{sinx}}=\boldsymbol{{x}}−\frac{\boldsymbol{{x}}^{\mathrm{3}} }{\mathrm{3}!}+\frac{\boldsymbol{{x}}^{\mathrm{5}} }{\mathrm{5}!}−...... \\ $$$$\boldsymbol{{so}}\:\:\:\:\:\:\frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}=\mathrm{1}−\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{3}!}+\frac{\boldsymbol{{x}}^{\mathrm{4}} }{\mathrm{5}!}−........ \\ $$$${now}\:\boldsymbol{{compare}}\:\boldsymbol{{the}}\:\boldsymbol{{x}}^{\mathrm{2}} \:\boldsymbol{{terms}}\:\boldsymbol{{both}} \\ $$$$\boldsymbol{{sides}}\:\boldsymbol{{of}}\:\boldsymbol{{the}}\:\boldsymbol{{eq}}^{\boldsymbol{{n}}} \:\left(\boldsymbol{{i}}\right)\:\boldsymbol{{we}}\:\boldsymbol{{will}}\:\boldsymbol{{get}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} \boldsymbol{\pi}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} \boldsymbol{\pi}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} \boldsymbol{\pi}^{\mathrm{2}} }+.....=\frac{\mathrm{1}}{\mathrm{3}!} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{finally}}\:\boldsymbol{{we}}\:\boldsymbol{{get}}: \\ $$$$\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }+....\infty=\boldsymbol{\zeta}\left(\mathrm{2}\right)=\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{6}}. \\ $$$$ \\ $$

Commented by I want to learn more last updated on 23/Jun/20

sir what of ζ(3) ???

$$\mathrm{sir}\:\mathrm{what}\:\mathrm{of}\:\:\zeta\left(\mathrm{3}\right)\:\:??? \\ $$

Commented by abdomathmax last updated on 23/Jun/20

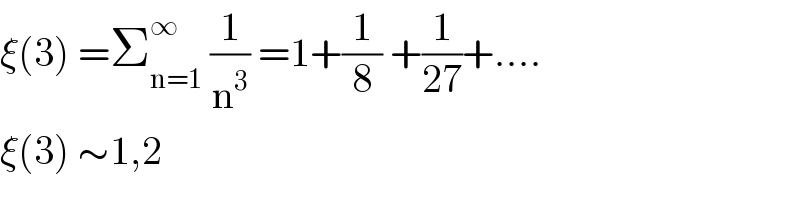
ξ(3) =Σ_(n=1) ^∞ (1/n^3 ) =1+(1/8) +(1/(27))+.... ξ(3) ∼1,2

$$\xi\left(\mathrm{3}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{27}}+.... \\ $$$$\xi\left(\mathrm{3}\right)\:\sim\mathrm{1},\mathrm{2} \\ $$

Commented by I want to learn more last updated on 23/Jun/20

Sir, please full workings.

$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{full}\:\mathrm{workings}. \\ $$

Commented by smridha last updated on 23/Jun/20

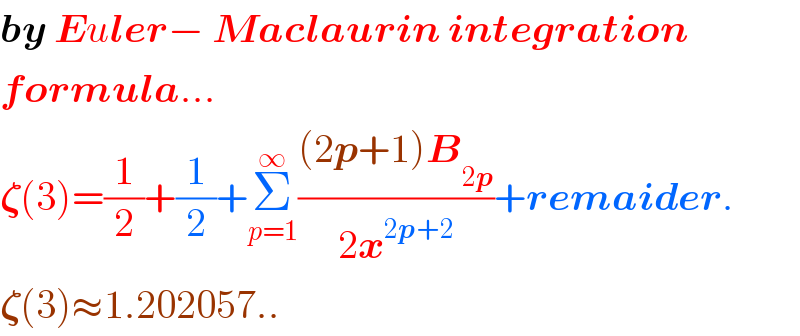
by Euler− Maclaurin integration formula... 𝛇(3)=(1/2)+(1/2)+Σ_(p=1) ^∞ (((2p+1)B_(2p) )/(2x^(2p+2) ))+remaider. 𝛇(3)≈1.202057..

$$\boldsymbol{{by}}\:\boldsymbol{{E}}{u}\boldsymbol{{ler}}−\:\boldsymbol{{Maclaurin}}\:\boldsymbol{{integration}} \\ $$$$\boldsymbol{{formula}}... \\ $$$$\boldsymbol{\zeta}\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\underset{{p}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}\boldsymbol{{p}}+\mathrm{1}\right)\boldsymbol{{B}}_{\mathrm{2}\boldsymbol{{p}}} }{\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}\boldsymbol{{p}}+\mathrm{2}} }+\boldsymbol{{remaider}}. \\ $$$$\boldsymbol{\zeta}\left(\mathrm{3}\right)\approx\mathrm{1}.\mathrm{202057}.. \\ $$

Commented by mathmax by abdo last updated on 23/Jun/20

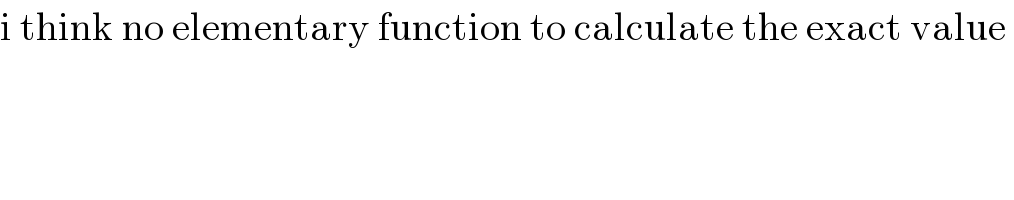
i think no elementary function to calculate the exact value

$$\mathrm{i}\:\mathrm{think}\:\mathrm{no}\:\mathrm{elementary}\:\mathrm{function}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{value}\: \\ $$

Commented by smridha last updated on 24/Jun/20

therefore I used ≈ instead of =.

$$\boldsymbol{{therefore}}\:\boldsymbol{{I}}\:\boldsymbol{{used}}\:\approx\:{in}\boldsymbol{{stead}}\:\boldsymbol{{of}} \\ $$$$=. \\ $$$$ \\ $$

Answered by abdomathmax last updated on 23/Jun/20

let f(x)=1 2π periodic odd let developp f at fourier serie f(x) =Σ_(n=1) ^∞ a_n sin(nx) a_n =(2/T)∫_([T]) sin(nx)dx =(1/π)∫_(−π) ^π sin(nx)dx =(2/π) ∫_0 ^π sin(nx)dx =−(2/π)[(1/n)cos(nx)]_0 ^π =−(2/(nπ)){ (−1)^n −1) ⇒ f(x) =Σ_(n=1) ^(∞ ) (2/(nπ))(1−(−1)^n )sin(nx) =(2/π) Σ_(n=0) ^∞ (2/(2n+1))sin(2n+1)x =1 ⇒ (4/π) Σ_(n=0) ^∞ ((sin(2n+1)x)/((2n+1))) =1 ⇒ Σ_(n=0) ^∞ ((sin(2n+1)x)/(2n+1)) =(π/4) let integrate ⇒ −Σ_(n=0) ^∞ ((cos(2n+1)x)/((2n+1)^2 )) =((πx)/4) +c x=0 ⇒−Σ_(n=0) ^∞ (1/((2n+1)^2 )) =c ⇒ ((πx)/4) =−Σ_(n=0) ^∞ ((cos(2n+1)x)/((2n+1)^2 ))+Σ_(n=0) ^∞ (1/((2n+1)^2 )) x=π ⇒(π^2 /4) =Σ_(n=0) ^∞ (1/((2n+1)^2 )) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(π^2 /8) we have Σ_(n=1) ^∞ (1/n^2 ) =(1/4)Σ_(n=1) ^∞ (1/n^2 ) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒(3/4)Σ_(n=1) ^∞ (1/n^2 ) =(π^2 /8) ⇒ Σ_(n=1) ^∞ (1/n^2 ) =(4/3)×(π^2 /8) Σ_(n=1) ^∞ (1/n^2 ) =(π^2 /6)

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}\:\:\mathrm{2}\pi\:\mathrm{periodic}\:\mathrm{odd}\:\mathrm{let}\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\: \\ $$$$\mathrm{fourier}\:\mathrm{serie}\:\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{a}_{\mathrm{n}} \mathrm{sin}\left(\mathrm{nx}\right) \\ $$$$\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{2}}{\mathrm{T}}\int_{\left[\mathrm{T}\right]} \:\mathrm{sin}\left(\mathrm{nx}\right)\mathrm{dx}\:=\frac{\mathrm{1}}{\pi}\int_{−\pi} ^{\pi} \:\mathrm{sin}\left(\mathrm{nx}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{2}}{\pi}\:\int_{\mathrm{0}} ^{\pi} \:\mathrm{sin}\left(\mathrm{nx}\right)\mathrm{dx}\:\:=−\frac{\mathrm{2}}{\pi}\left[\frac{\mathrm{1}}{\mathrm{n}}\mathrm{cos}\left(\mathrm{nx}\right)\right]_{\mathrm{0}} ^{\pi} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{n}\pi}\left\{\:\left(−\mathrm{1}\right)^{\mathrm{n}} −\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty\:} \:\frac{\mathrm{2}}{\mathrm{n}\pi}\left(\mathrm{1}−\left(−\mathrm{1}\right)^{\mathrm{n}} \right)\mathrm{sin}\left(\mathrm{nx}\right) \\ $$$$=\frac{\mathrm{2}}{\pi}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}}{\mathrm{2n}+\mathrm{1}}\mathrm{sin}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}\:=\mathrm{1}\:\Rightarrow \\ $$$$\frac{\mathrm{4}}{\pi}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}}{\left(\mathrm{2n}+\mathrm{1}\right)}\:=\mathrm{1}\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}}{\mathrm{2n}+\mathrm{1}}\:=\frac{\pi}{\mathrm{4}}\:\:\mathrm{let}\:\mathrm{integrate}\:\Rightarrow \\ $$$$−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\pi\mathrm{x}}{\mathrm{4}}\:+\mathrm{c} \\ $$$$\mathrm{x}=\mathrm{0}\:\Rightarrow−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{c}\:\Rightarrow \\ $$$$\frac{\pi\mathrm{x}}{\mathrm{4}}\:=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{x}=\pi\:\Rightarrow\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{3}}{\mathrm{4}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:=\frac{\mathrm{4}}{\mathrm{3}}×\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com