
Previous in Relation and Functions Next in Relation and Functions
Question Number 200722 by cortano12 last updated on 22/Nov/23
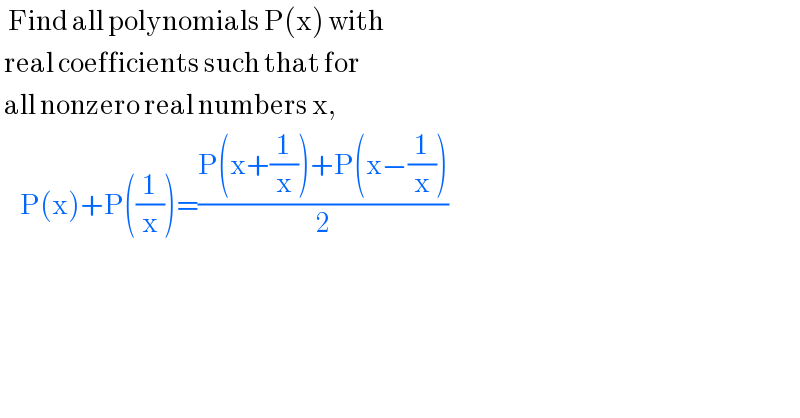
$$\:\:\mathrm{Find}\:\mathrm{all}\:\mathrm{polynomials}\:\mathrm{P}\left(\mathrm{x}\right)\:\mathrm{with} \\ $$$$\:\mathrm{real}\:\mathrm{coefficients}\:\mathrm{such}\:\mathrm{that}\:\mathrm{for} \\ $$$$\:\mathrm{all}\:\mathrm{nonzero}\:\mathrm{real}\:\mathrm{numbers}\:\mathrm{x},\: \\ $$$$\:\:\:\:\:\mathrm{P}\left(\mathrm{x}\right)+\mathrm{P}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\frac{\mathrm{P}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{P}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{2}}\:\:\: \\ $$
Commented by Frix last updated on 22/Nov/23
![P(x)=ax^2 [∨P(x)=0]](Q200732.png)
$${P}\left({x}\right)={ax}^{\mathrm{2}} \:\:\:\:\:\left[\vee{P}\left({x}\right)=\mathrm{0}\right] \\ $$
Answered by witcher3 last updated on 22/Nov/23
![x→^f x−(1/x); ]0,+∞[→]−∞,+∞[ bijective p((1/x))+p(x)=(1/2)(p(x+(1/x))+p(−x+(1/x))=(1/2)(p(x+(1/x))+p(x−(1/x))) ⇒p(x−(1/x))=p(−((1/x)−x)) ⇔∀a∈R since bijectiln of f. p(a)=p(−a)⇒ p(x)=Σ_(k=0) ^n a_k x^(2k) ;p∈R_(2n) [X] x=e^t , p(e^t )+p(e^(−t) )=(1/2)p(2ch(t))+p(2sh(t)) ⇔2p(e^t )+2p(e^(−t) )=p(2ch(t))+p(2sh(t)) ⇔4Σ_(k=0) ^(2n) a_k ch(2kt)=Σ_(k=0) ^(2n) a_k 2^(2k) (ch^(2k) (t)+sh^(2k) (t)) ⇔∀k∈[0,2] 4ch(2kt)=2^(2k) (ch^(2k) (t)+sh^(2k) (t) k=1 true ,∀k≥2 4ch(2kt)=2^(2k) (ch^(2k) (t)+sh^(2k) (t);t=0 4=2^(2k) false k≥2 ⇒p(x)=a_0 +a_1 x^2 ;p(1)+p((1/1))=(1/2)(p(2)+p(0)) ⇔2(a_0 +a_1 )=a_0 +2a_1 a_0 =0 p(x)=ax^2 worck unique by construcrion ;a∈R](Q200757.png)
$$\mathrm{x}\overset{\mathrm{f}} {\rightarrow}\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}; \\ $$$$\left.\right]\mathrm{0},+\infty\left[\rightarrow\right]−\infty,+\infty\left[\:\mathrm{bijective}\right. \\ $$$$\mathrm{p}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{p}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{p}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{p}\left(−\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{p}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{p}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)\right)\right. \\ $$$$\Rightarrow\mathrm{p}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{p}\left(−\left(\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{x}\right)\right) \\ $$$$\Leftrightarrow\forall\mathrm{a}\in\mathbb{R}\:\mathrm{since}\:\mathrm{bijectiln}\:\mathrm{of}\:\mathrm{f}.\:\mathrm{p}\left(\mathrm{a}\right)=\mathrm{p}\left(−\mathrm{a}\right)\Rightarrow \\ $$$$\mathrm{p}\left(\mathrm{x}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{k}} \mathrm{x}^{\mathrm{2k}} ;\mathrm{p}\in\mathbb{R}_{\mathrm{2n}} \left[\mathrm{X}\right] \\ $$$$\mathrm{x}=\mathrm{e}^{\mathrm{t}} , \\ $$$$\mathrm{p}\left(\mathrm{e}^{\mathrm{t}} \right)+\mathrm{p}\left(\mathrm{e}^{−\mathrm{t}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{p}\left(\mathrm{2ch}\left(\mathrm{t}\right)\right)+\mathrm{p}\left(\mathrm{2sh}\left(\mathrm{t}\right)\right) \\ $$$$\Leftrightarrow\mathrm{2p}\left(\mathrm{e}^{\mathrm{t}} \right)+\mathrm{2p}\left(\mathrm{e}^{−\mathrm{t}} \right)=\mathrm{p}\left(\mathrm{2ch}\left(\mathrm{t}\right)\right)+\mathrm{p}\left(\mathrm{2sh}\left(\mathrm{t}\right)\right) \\ $$$$\Leftrightarrow\mathrm{4}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\mathrm{a}_{\mathrm{k}} \mathrm{ch}\left(\mathrm{2kt}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\mathrm{a}_{\mathrm{k}} \mathrm{2}^{\mathrm{2k}} \left(\mathrm{ch}^{\mathrm{2k}} \left(\mathrm{t}\right)+\mathrm{sh}^{\mathrm{2k}} \left(\mathrm{t}\right)\right) \\ $$$$\Leftrightarrow\forall\mathrm{k}\in\left[\mathrm{0},\mathrm{2}\right] \\ $$$$\mathrm{4ch}\left(\mathrm{2kt}\right)=\mathrm{2}^{\mathrm{2k}} \left(\mathrm{ch}^{\mathrm{2k}} \left(\mathrm{t}\right)+\mathrm{sh}^{\mathrm{2k}} \left(\mathrm{t}\right)\right. \\ $$$$\mathrm{k}=\mathrm{1}\:\mathrm{true}\:,\forall\mathrm{k}\geqslant\mathrm{2} \\ $$$$\mathrm{4ch}\left(\mathrm{2kt}\right)=\mathrm{2}^{\mathrm{2k}} \left(\mathrm{ch}^{\mathrm{2k}} \left(\mathrm{t}\right)+\mathrm{sh}^{\mathrm{2k}} \left(\mathrm{t}\right);\mathrm{t}=\mathrm{0}\right. \\ $$$$\mathrm{4}=\mathrm{2}^{\mathrm{2k}} \:\mathrm{false}\:\mathrm{k}\geqslant\mathrm{2} \\ $$$$\Rightarrow\mathrm{p}\left(\mathrm{x}\right)=\mathrm{a}_{\mathrm{0}} +\mathrm{a}_{\mathrm{1}} \mathrm{x}^{\mathrm{2}} \:;\mathrm{p}\left(\mathrm{1}\right)+\mathrm{p}\left(\frac{\mathrm{1}}{\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{p}\left(\mathrm{2}\right)+\mathrm{p}\left(\mathrm{0}\right)\right) \\ $$$$\Leftrightarrow\mathrm{2}\left(\mathrm{a}_{\mathrm{0}} +\mathrm{a}_{\mathrm{1}} \right)=\mathrm{a}_{\mathrm{0}} +\mathrm{2a}_{\mathrm{1}} \\ $$$$\mathrm{a}_{\mathrm{0}} =\mathrm{0} \\ $$$$\mathrm{p}\left(\mathrm{x}\right)=\mathrm{ax}^{\mathrm{2}} \:\mathrm{worck}\:\mathrm{unique}\:\mathrm{by}\:\mathrm{construcrion} \\ $$$$;\mathrm{a}\in\mathbb{R} \\ $$
