Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 188301 by mr W last updated on 28/Feb/23

Find the number of triangles with integer side lengths and perimeter p.

$${Find}\:{the}\:{number}\:{of}\:{triangles}\:{with} \\ $$$${integer}\:{side}\:{lengths}\:{and}\:{perimeter}\:{p}. \\ $$

Commented by mr W last updated on 28/Feb/23

as Q188239, but in general case.

$${as}\:{Q}\mathrm{188239},\:{but}\:{in}\:{general}\:{case}. \\ $$

Commented by BaliramKumar last updated on 27/Feb/23

why

$${why} \\ $$

Commented by mr W last updated on 27/Feb/23

for more solutions!

$${for}\:{more}\:{solutions}! \\ $$

Commented by mr W last updated on 27/Feb/23

if you have a solution, please share.

$${if}\:{you}\:{have}\:{a}\:{solution},\:{please}\:{share}. \\ $$

Answered by mr W last updated on 04/Mar/23

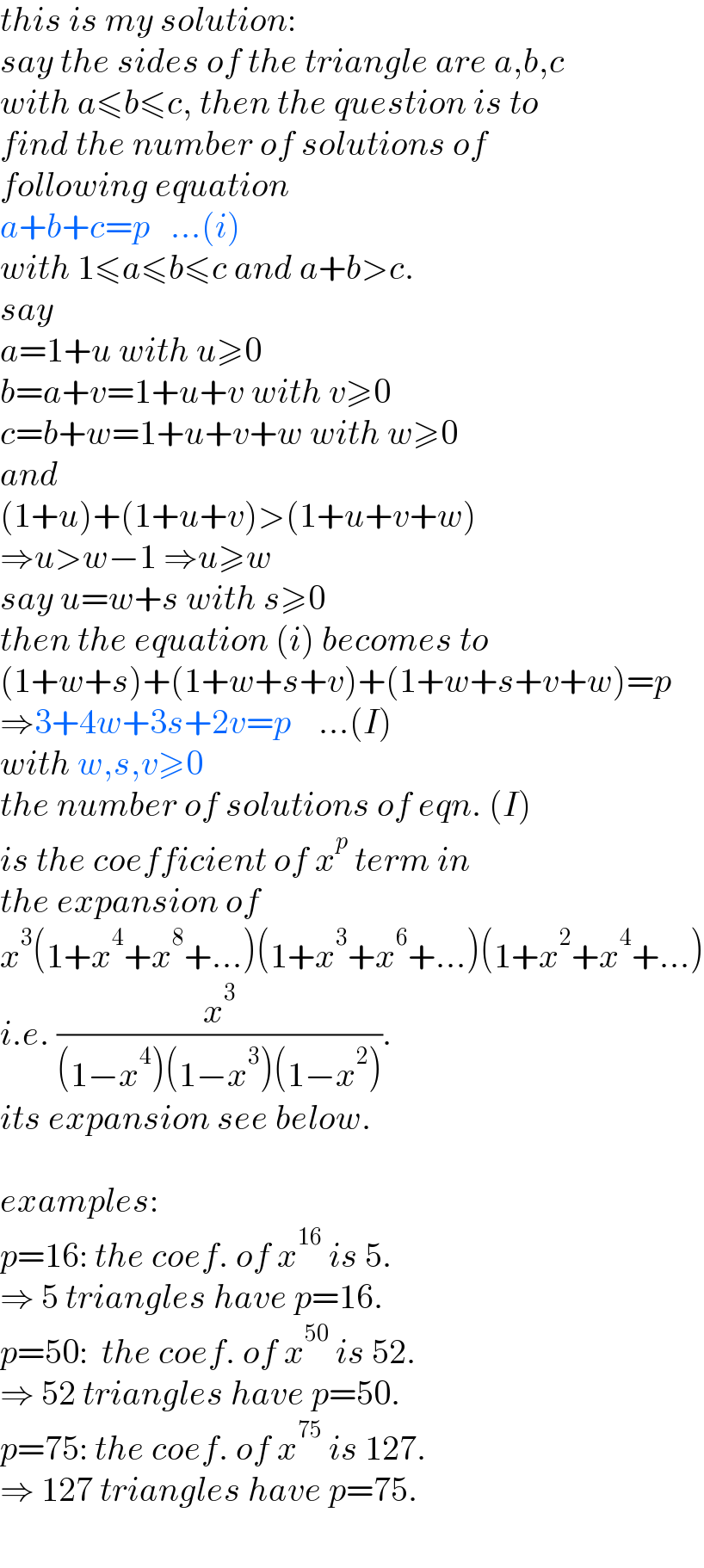
this is my solution: say the sides of the triangle are a,b,c with a≤b≤c, then the question is to find the number of solutions of following equation a+b+c=p ...(i) with 1≤a≤b≤c and a+b>c. say a=1+u with u≥0 b=a+v=1+u+v with v≥0 c=b+w=1+u+v+w with w≥0 and (1+u)+(1+u+v)>(1+u+v+w) ⇒u>w−1 ⇒u≥w say u=w+s with s≥0 then the equation (i) becomes to (1+w+s)+(1+w+s+v)+(1+w+s+v+w)=p ⇒3+4w+3s+2v=p ...(I) with w,s,v≥0 the number of solutions of eqn. (I) is the coefficient of x^p term in the expansion of x^3 (1+x^4 +x^8 +...)(1+x^3 +x^6 +...)(1+x^2 +x^4 +...) i.e. (x^3 /((1−x^4 )(1−x^3 )(1−x^2 ))). its expansion see below. examples: p=16: the coef. of x^(16) is 5. ⇒ 5 triangles have p=16. p=50: the coef. of x^(50) is 52. ⇒ 52 triangles have p=50. p=75: the coef. of x^(75) is 127. ⇒ 127 triangles have p=75.

$${this}\:{is}\:{my}\:{solution}: \\ $$$${say}\:{the}\:{sides}\:{of}\:{the}\:{triangle}\:{are}\:{a},{b},{c} \\ $$$${with}\:{a}\leqslant{b}\leqslant{c},\:{then}\:{the}\:{question}\:{is}\:{to}\: \\ $$$${find}\:{the}\:{number}\:{of}\:{solutions}\:{of}\: \\ $$$${following}\:{equation} \\ $$$${a}+{b}+{c}={p}\:\:\:...\left({i}\right) \\ $$$${with}\:\mathrm{1}\leqslant{a}\leqslant{b}\leqslant{c}\:{and}\:{a}+{b}>{c}. \\ $$$${say} \\ $$$${a}=\mathrm{1}+{u}\:{with}\:{u}\geqslant\mathrm{0} \\ $$$${b}={a}+{v}=\mathrm{1}+{u}+{v}\:{with}\:{v}\geqslant\mathrm{0} \\ $$$${c}={b}+{w}=\mathrm{1}+{u}+{v}+{w}\:{with}\:{w}\geqslant\mathrm{0} \\ $$$${and} \\ $$$$\left(\mathrm{1}+{u}\right)+\left(\mathrm{1}+{u}+{v}\right)>\left(\mathrm{1}+{u}+{v}+{w}\right) \\ $$$$\Rightarrow{u}>{w}−\mathrm{1}\:\Rightarrow{u}\geqslant{w} \\ $$$${say}\:{u}={w}+{s}\:{with}\:{s}\geqslant\mathrm{0} \\ $$$${then}\:{the}\:{equation}\:\left({i}\right)\:{becomes}\:{to} \\ $$$$\left(\mathrm{1}+{w}+{s}\right)+\left(\mathrm{1}+{w}+{s}+{v}\right)+\left(\mathrm{1}+{w}+{s}+{v}+{w}\right)={p} \\ $$$$\Rightarrow\mathrm{3}+\mathrm{4}{w}+\mathrm{3}{s}+\mathrm{2}{v}={p}\:\:\:\:...\left({I}\right) \\ $$$${with}\:{w},{s},{v}\geqslant\mathrm{0} \\ $$$${the}\:{number}\:{of}\:{solutions}\:{of}\:{eqn}.\:\left({I}\right) \\ $$$${is}\:{the}\:{coefficient}\:{of}\:{x}^{{p}} \:{term}\:{in} \\ $$$${the}\:{expansion}\:{of} \\ $$$${x}^{\mathrm{3}} \left(\mathrm{1}+{x}^{\mathrm{4}} +{x}^{\mathrm{8}} +...\right)\left(\mathrm{1}+{x}^{\mathrm{3}} +{x}^{\mathrm{6}} +...\right)\left(\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} +...\right) \\ $$$${i}.{e}.\:\frac{{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}^{\mathrm{4}} \right)\left(\mathrm{1}−{x}^{\mathrm{3}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}. \\ $$$${its}\:{expansion}\:{see}\:{below}. \\ $$$$ \\ $$$${examples}: \\ $$$${p}=\mathrm{16}:\:{the}\:{coef}.\:{of}\:{x}^{\mathrm{16}} \:{is}\:\mathrm{5}. \\ $$$$\Rightarrow\:\mathrm{5}\:{triangles}\:{have}\:{p}=\mathrm{16}. \\ $$$${p}=\mathrm{50}:\:\:{the}\:{coef}.\:{of}\:{x}^{\mathrm{50}} \:{is}\:\mathrm{52}. \\ $$$$\Rightarrow\:\mathrm{52}\:{triangles}\:{have}\:{p}=\mathrm{50}. \\ $$$${p}=\mathrm{75}:\:{the}\:{coef}.\:{of}\:{x}^{\mathrm{75}} \:{is}\:\mathrm{127}. \\ $$$$\Rightarrow\:\mathrm{127}\:{triangles}\:{have}\:{p}=\mathrm{75}. \\ $$

Commented by mr W last updated on 04/Mar/23

Commented by manxsol last updated on 27/Feb/23

Bravo, Sir W. Great work . thanks for the explanation

$${Bravo},\:{Sir}\:{W}.\:{Great}\:{work}\:. \\ $$$${thanks}\:{for}\:{the}\:{explanation} \\ $$

Commented by mr W last updated on 28/Feb/23

this is a question in the number theory about the partition of an integer.

$${this}\:{is}\:{a}\:{question}\:{in}\:{the}\:{number}\: \\ $$$${theory}\:{about}\:{the}\:{partition}\:{of}\:{an}\: \\ $$$${integer}. \\ $$

Commented by mr W last updated on 28/Feb/23

Commented by BaliramKumar last updated on 28/Feb/23

Great Sir

$${Great}\:{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com