Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 203832 by depressiveshrek last updated on 29/Jan/24

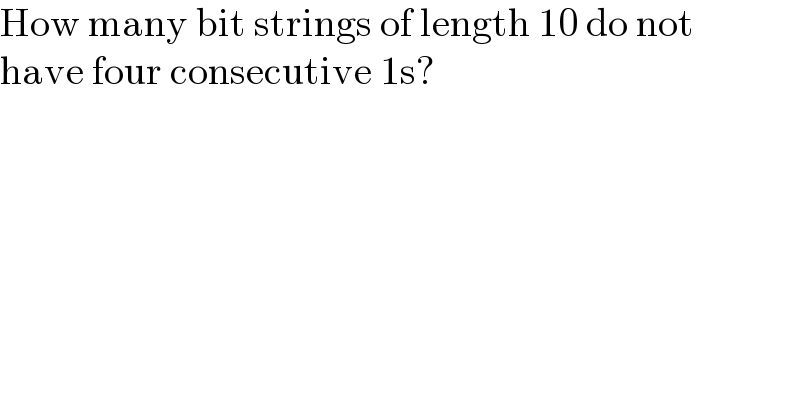
How many bit strings of length 10 do not have four consecutive 1s?

$$\mathrm{How}\:\mathrm{many}\:\mathrm{bit}\:\mathrm{strings}\:\mathrm{of}\:\mathrm{length}\:\mathrm{10}\:\mathrm{do}\:\mathrm{not} \\ $$$$\mathrm{have}\:\mathrm{four}\:\mathrm{consecutive}\:\mathrm{1s}? \\ $$

Answered by nikif99 last updated on 30/Jan/24

Total number of bit strings of length 10 is 2^(10) =1024 (0−1023). Of them, there are 7 bit strings of exactly 4 ′1′s at posihions 1−7. 001111_() 0000 Furthermore, there are 3 bit strings of more than one ′1111′: 1111011110 1111001111 0111101111 Answer: 1024−7−3=1014

$${Total}\:{number}\:{of}\:{bit}\:{strings}\:{of}\:{length}\:\mathrm{10} \\ $$$${is}\:\mathrm{2}^{\mathrm{10}} =\mathrm{1024}\:\left(\mathrm{0}−\mathrm{1023}\right). \\ $$$${Of}\:{them},\:{there}\:{are}\:\mathrm{7}\:{bit}\:{strings}\:{of} \\ $$$${exactly}\:\mathrm{4}\:'\mathrm{1}'{s}\:{at}\:{posihions}\:\mathrm{1}−\mathrm{7}. \\ $$$$\mathrm{00}\underset{} {\underbrace{\mathrm{1111}}0000} \\ $$$${Furthermore},\:{there}\:{are}\:\mathrm{3}\:{bit}\:{strings} \\ $$$${of}\:{more}\:{than}\:{one}\:'\mathrm{1111}': \\ $$$$\mathrm{1111011110} \\ $$$$\mathrm{1111001111} \\ $$$$\mathrm{0111101111} \\ $$$${Answer}:\:\mathrm{1024}−\mathrm{7}−\mathrm{3}=\mathrm{1014} \\ $$

Commented by deleteduser1 last updated on 30/Jan/24

It seems 1011110000, 1110111100,etc should also be valid for those containing the string 1111

$${It}\:{seems}\:\mathrm{1011110000},\:\mathrm{1110111100},{etc}\:{should} \\ $$$${also}\:{be}\:{valid}\:{for}\:{those}\:{containing}\:{the}\:{string} \\ $$$$\mathrm{1111} \\ $$

Commented by nikif99 last updated on 30/Jan/24

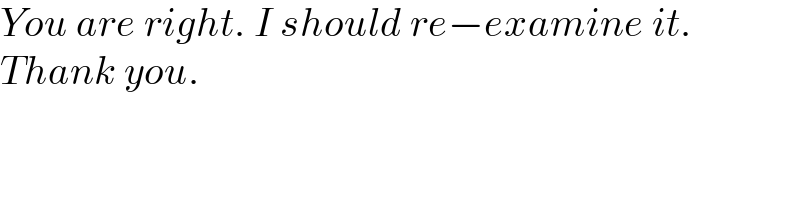
You are right. I should re−examine it. Thank you.

$${You}\:{are}\:{right}.\:{I}\:{should}\:{re}−{examine}\:{it}. \\ $$$${Thank}\:{you}. \\ $$

Commented by nikif99 last updated on 30/Jan/24

Re−evaluating my computations: In a 10−bit string, I fix a series of 4 consecutive ′1′s ensuring adjacent bits (if exixt) are set to 0. Example: 0011110000 where reds are set to 1, blues are set to 0 to prohibit expansion of reds and blacks derive a 4−bit set with values 0 to 15. So, we have next options. a) 1111000000_() (32 cases) b) 0111100000_() (16) c) 0011110000 (16) d) 0001111000 (16) e) 0000111100 (16) f) 0000011110 (16) g) 0000001111 (32) total 32×2+16×5=144 minus 2 for 0111101111 and 1111001111 which are double counted=142 with 4 concecutive ′1′s. Non consecutive ones are 1024−142=882

$${Re}−{evaluating}\:{my}\:{computations}: \\ $$$${In}\:{a}\:\mathrm{10}−{bit}\:{string},\:{I}\:{fix}\:{a}\:{series}\:{of} \\ $$$$\mathrm{4}\:{consecutive}\:'\mathrm{1}'{s}\:{ensuring}\:{adjacent} \\ $$$${bits}\:\left({if}\:{exixt}\right)\:{are}\:{set}\:{to}\:\mathrm{0}.\:{Example}: \\ $$$$\mathrm{0011110000}\:{where} \\ $$$${reds}\:{are}\:{set}\:{to}\:\mathrm{1},\:{blues}\:{are}\:{set}\:{to}\:\mathrm{0}\:{to} \\ $$$${prohibit}\:{expansion}\:{of}\:{reds}\:{and}\:{blacks} \\ $$$${derive}\:{a}\:\mathrm{4}−{bit}\:{set}\:{with}\:{values}\:\mathrm{0}\:{to}\:\mathrm{15}. \\ $$$${So},\:{we}\:{have}\:{next}\:{options}. \\ $$$$\left.{a}\right)\:\mathrm{11110}\underset{} {\underbrace{\mathrm{00000}}}\:\left(\mathrm{32}\:{cases}\right) \\ $$$$\left.{b}\right)\:\mathrm{011110}\underset{} {\underbrace{\mathrm{0000}}}\:\left(\mathrm{16}\right) \\ $$$$\left.{c}\right)\:\mathrm{0011110000}\:\left(\mathrm{16}\right) \\ $$$$\left.{d}\right)\:\mathrm{0001111000}\:\left(\mathrm{16}\right) \\ $$$$\left.{e}\right)\:\mathrm{0000111100}\:\left(\mathrm{16}\right) \\ $$$$\left.{f}\right)\:\mathrm{0000011110}\:\left(\mathrm{16}\right) \\ $$$$\left.{g}\right)\:\mathrm{0000001111}\:\left(\mathrm{32}\right) \\ $$$${total}\:\mathrm{32}×\mathrm{2}+\mathrm{16}×\mathrm{5}=\mathrm{144} \\ $$$${minus}\:\mathrm{2}\:{for}\:\mathrm{0111101111}\:{and}\:\mathrm{1111001111} \\ $$$${which}\:{are}\:{double}\:{counted}=\mathrm{142}\:\boldsymbol{{with}}\:\mathrm{4} \\ $$$${concecutive}\:'\mathrm{1}'{s}. \\ $$$$\boldsymbol{{Non}}\:{consecutive}\:{ones}\:{are} \\ $$$$\mathrm{1024}−\mathrm{142}=\mathrm{882} \\ $$

Commented by deleteduser1 last updated on 31/Jan/24

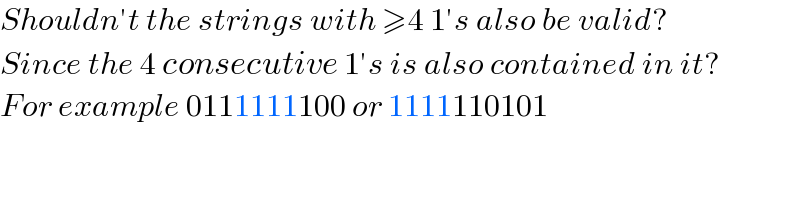
Shouldn′t the strings with ≥4 1′s also be valid? Since the 4 consecutive 1′s is also contained in it? For example 0111111100 or 1111110101

$${Shouldn}'{t}\:{the}\:{strings}\:{with}\:\geqslant\mathrm{4}\:\mathrm{1}'{s}\:{also}\:{be}\:{valid}? \\ $$$${Since}\:{the}\:\mathrm{4}\:{consecutive}\:\mathrm{1}'{s}\:{is}\:{also}\:{contained}\:{in}\:{it}? \\ $$$${For}\:{example}\:\mathrm{0111111100}\:{or}\:\mathrm{1111110101} \\ $$

Commented by nikif99 last updated on 30/Jan/24

The question is “do not have 4 consecuhive 1s”, 0111111100 has 7, so I consider is not contained. That′s why I blocked neighbouring places with 0.

$${The}\:{question}\:{is}\:``{do}\:{not}\:{have}\:\mathrm{4}\: \\ $$$${consecuhive}\:\mathrm{1}{s}'',\:\mathrm{0111111100}\:{has}\:\mathrm{7}, \\ $$$${so}\:{I}\:{consider}\:{is}\:{not}\:{contained}. \\ $$$${That}'{s}\:{why}\:{I}\:{blocked}\:{neighbouring} \\ $$$${places}\:{with}\:\mathrm{0}. \\ $$

Commented by deleteduser1 last updated on 30/Jan/24

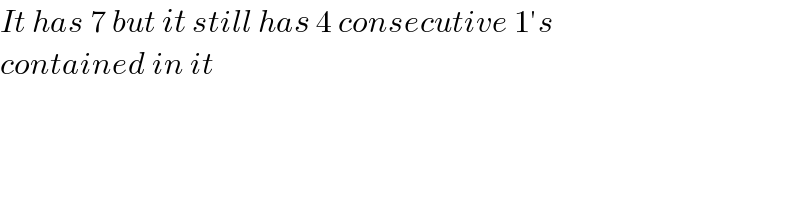
It has 7 but it still has 4 consecutive 1′s contained in it

$${It}\:{has}\:\mathrm{7}\:{but}\:{it}\:{still}\:{has}\:\mathrm{4}\:{consecutive}\:\mathrm{1}'{s}\: \\ $$$${contained}\:{in}\:{it} \\ $$

Answered by deleteduser1 last updated on 31/Jan/24

Case1: 1111 _ _ _ _ _ _ ⇒2^6 ways Case 2: __1 1111_ _ _ _ _ ⇒2^5 ×1 ways and __1 =0 Case 3: __1 __2 1111_ _ _ _ Possible for (__1 ,__2 )=(1,1),(1,0),(0,1),(0,0) Of this, only (1,0)∧(0,0) haven′t been accounted for in cases 1 and 2⇒#(Case 3)=2×2^4 =2^5 ways Case 4: __1 __2 __3 1111_ _ _ Possible: (0,0,0),(0,0,1),(0,1,0),(1,0,0),(0,1,1) (1,0,1),(1,1,0) Similarly, we get #(Case 4)=4×2^3 =2^5 ways Case 5: __1 __2 __3 __4 1111_ _ ⇒2^3 ×2^2 =2^5 ways Case 6: __1 __2 __3 __4 __5 1111 _ Other than case 1, __5 always contained 1 ⇒#(Case 6)=2^4 ×2−2=30 ways Case 7: __1 __2 __3 __4 __5 __6 1111 __6 =0 and __1 __2 __3 __4 __(5 ) is such that it contains no 4 consecutive 1′s(11110,01111,11111) ⇒#(Case 7)= 2^5 −3=29 ⇒#(contains 4 consecutive 1′s)=251 ⇒#(doesn′t contain 4 consecutive 1′s)=1024−252 =773

$${Case}\mathrm{1}:\:\mathrm{1111}\:\_\:\_\:\_\:\_\:\_\:\_\:\Rightarrow\mathrm{2}^{\mathrm{6}} \:{ways} \\ $$$${Case}\:\mathrm{2}:\:\__{\mathrm{1}} \:\mathrm{1111\_}\:\_\:\_\:\_\:\_\:\Rightarrow\mathrm{2}^{\mathrm{5}} ×\mathrm{1}\:{ways}\:{and}\:\__{\mathrm{1}} =\mathrm{0} \\ $$$${Case}\:\mathrm{3}:\:\__{\mathrm{1}} \:\__{\mathrm{2}} \:\mathrm{1111\_}\:\_\:\_\:\_\: \\ $$$${Possible}\:{for}\:\left(\__{\mathrm{1}} ,\__{\mathrm{2}} \right)=\left(\mathrm{1},\mathrm{1}\right),\left(\mathrm{1},\mathrm{0}\right),\left(\mathrm{0},\mathrm{1}\right),\left(\mathrm{0},\mathrm{0}\right)\: \\ $$$${Of}\:{this},\:{only}\:\left(\mathrm{1},\mathrm{0}\right)\wedge\left(\mathrm{0},\mathrm{0}\right)\:{haven}'{t}\:{been}\:{accounted} \\ $$$${for}\:{in}\:{cases}\:\mathrm{1}\:{and}\:\mathrm{2}\Rightarrow#\left({Case}\:\mathrm{3}\right)=\mathrm{2}×\mathrm{2}^{\mathrm{4}} =\mathrm{2}^{\mathrm{5}} \:{ways} \\ $$$${Case}\:\mathrm{4}:\:\__{\mathrm{1}} \:\__{\mathrm{2}} \:\__{\mathrm{3}} \:\mathrm{1111\_}\:\_\:\_ \\ $$$${Possible}:\:\left(\mathrm{0},\mathrm{0},\mathrm{0}\right),\left(\mathrm{0},\mathrm{0},\mathrm{1}\right),\left(\mathrm{0},\mathrm{1},\mathrm{0}\right),\left(\mathrm{1},\mathrm{0},\mathrm{0}\right),\left(\mathrm{0},\mathrm{1},\mathrm{1}\right) \\ $$$$\left(\mathrm{1},\mathrm{0},\mathrm{1}\right),\left(\mathrm{1},\mathrm{1},\mathrm{0}\right) \\ $$$${Similarly},\:{we}\:{get}\:#\left({Case}\:\mathrm{4}\right)=\mathrm{4}×\mathrm{2}^{\mathrm{3}} =\mathrm{2}^{\mathrm{5}} \:{ways} \\ $$$${Case}\:\mathrm{5}:\:\__{\mathrm{1}} \:\__{\mathrm{2}} \:\__{\mathrm{3}} \:\__{\mathrm{4}} \mathrm{1111\_}\:\_\:\Rightarrow\mathrm{2}^{\mathrm{3}} ×\mathrm{2}^{\mathrm{2}} =\mathrm{2}^{\mathrm{5}} \:{ways} \\ $$$${Case}\:\mathrm{6}:\:\__{\mathrm{1}} \:\__{\mathrm{2}} \:\__{\mathrm{3}} \:\__{\mathrm{4}} \:\__{\mathrm{5}} \:\mathrm{1111}\:\_ \\ $$$${Other}\:{than}\:{case}\:\mathrm{1},\:\__{\mathrm{5}} \:{always}\:{contained}\:\mathrm{1} \\ $$$$\Rightarrow#\left({Case}\:\mathrm{6}\right)=\mathrm{2}^{\mathrm{4}} ×\mathrm{2}−\mathrm{2}=\mathrm{30}\:{ways} \\ $$$${Case}\:\mathrm{7}:\:\__{\mathrm{1}} \:\__{\mathrm{2}} \:\__{\mathrm{3}} \:\__{\mathrm{4}} \:\__{\mathrm{5}} \:\__{\mathrm{6}} \mathrm{1111} \\ $$$$\__{\mathrm{6}} =\mathrm{0}\:{and}\:\__{\mathrm{1}} \__{\mathrm{2}} \__{\mathrm{3}} \__{\mathrm{4}} \__{\mathrm{5}\:} {is}\:{such}\:{that}\:{it}\:{contains}\:{no} \\ $$$$\mathrm{4}\:{consecutive}\:\mathrm{1}'{s}\left(\mathrm{11110},\mathrm{01111},\mathrm{11111}\right) \\ $$$$\Rightarrow#\left({Case}\:\mathrm{7}\right)=\:\mathrm{2}^{\mathrm{5}} −\mathrm{3}=\mathrm{29} \\ $$$$\Rightarrow#\left({contains}\:\mathrm{4}\:{consecutive}\:\mathrm{1}'{s}\right)=\mathrm{251} \\ $$$$\Rightarrow#\left({doesn}'{t}\:{contain}\:\mathrm{4}\:{consecutive}\:\mathrm{1}'{s}\right)=\mathrm{1024}−\mathrm{252} \\ $$$$=\mathrm{773} \\ $$

Commented by nikif99 last updated on 31/Jan/24

Good and clear explanation.

$${Good}\:{and}\:{clear}\:{explanation}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com