
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 189021 by mr W last updated on 10/Mar/23

$${How}\:{many}\:{non}−{similar}\:{triangles} \\ $$$${have}\:{integer}\:{angles}\:{in}\:°? \\ $$
Commented by nikif99 last updated on 11/Mar/23
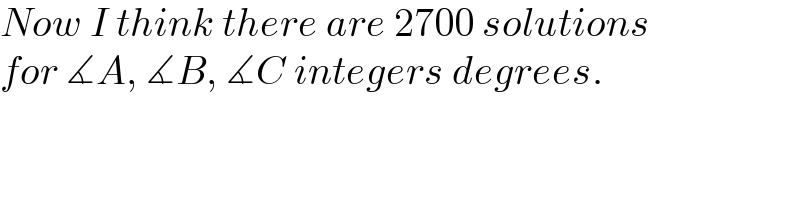
$${Now}\:{I}\:{think}\:{there}\:{are}\:\mathrm{2700}\:{solutions}\: \\ $$$${for}\:\measuredangle{A},\:\measuredangle{B},\:\measuredangle{C}\:{integers}\:{degrees}. \\ $$
Commented by mr W last updated on 11/Mar/23

$${that}'{s}\:{correct}.\:{can}\:{you}\:{share}\:{how} \\ $$$${you}\:{got}\:{this}\:{result}? \\ $$
Commented by nikif99 last updated on 11/Mar/23

$$\measuredangle{A}\:{takes}\:{values}\:\mathrm{1}\:{to}\:\mathrm{60}\:\left({to}\:{avoid}\:\right. \\ $$$$\left.{circular}\:{repetitions}\right),\:\measuredangle{B}\:{takes}\: \\ $$$${values}\:{from}\:{A}\:{to}\:{int}\left(\frac{\mathrm{180}−{A}}{\mathrm{2}}\right)\:{and} \\ $$$$\measuredangle{C}\:{the}\:{rest}\:{till}\:\mathrm{180}. \\ $$$$\measuredangle{A}=\mathrm{1}\:\:\:\measuredangle{B}=\mathrm{1}\:{to}\:\mathrm{89}\:\:\mathrm{89}\:{cases} \\ $$$$\measuredangle{A}=\mathrm{2}\:\:\:\measuredangle{B}=\mathrm{2}\:{to}\:\mathrm{89}\:\:\mathrm{88}\:{cases} \\ $$$$\measuredangle{A}=\mathrm{3}\:\:\:\measuredangle{B}=\mathrm{3}\:{to}\:\mathrm{88}\:\:\mathrm{86}\:{cases}\:\left({missing}\:\mathrm{87}\right) \\ $$$$\measuredangle{A}=\mathrm{4}\:\:\:\measuredangle{B}=\mathrm{4}\:{to}\:\mathrm{88}\:\:\mathrm{85}\:{cases} \\ $$$$\measuredangle{A}=\mathrm{5}\:\:\:\measuredangle{B}=\mathrm{5}\:{to}\:\mathrm{87}\:\:\mathrm{83}\:{cases}\:\left({missing}\:\mathrm{84}\right) \\ $$$$... \\ $$$$\measuredangle{A}=\mathrm{58}\:\:\:\measuredangle{B}=\mathrm{58}\:{to}\:\mathrm{61}\:\:\mathrm{4}\:{cases} \\ $$$$\measuredangle{A}=\mathrm{59}\:\:\:\measuredangle{B}=\mathrm{59}\:{to}\:\mathrm{60}\:\:\mathrm{2}\:{cases}\:\left({missing}\:\mathrm{3}\right) \\ $$$$\measuredangle{A}=\mathrm{60}\:\:\:\measuredangle{B}=\mathrm{60}\:{to}\:\mathrm{60}\:\:\mathrm{1}\:{case} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{89}} {\sum}}=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}=\mathrm{4005} \\ $$$${less}\:{cases}\:\mathrm{87}−\mathrm{84}−\mathrm{81}−...−\mathrm{6}−\mathrm{3}= \\ $$$$\mathrm{3}\underset{{n}=\mathrm{1}} {\overset{\mathrm{29}} {\sum}}=\mathrm{1305}\:\Rightarrow{real}\:{cases}=\mathrm{4005}−\mathrm{1305}=\mathrm{2700} \\ $$
Commented by mr W last updated on 11/Mar/23

$${thanks}\:{alot}\:{for}\:{your}\:{nice}\:{solution}! \\ $$
Answered by nikif99 last updated on 11/Mar/23

$$\mathrm{675}\:{found}\:{using}\: \\ $$$$\mathrm{sin}\:{A}+\mathrm{sin}\:{B}+\mathrm{sin}\:{C}=\mathrm{4cos}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{C}}{\mathrm{2}} \\ $$$${and}\:{triangle}\:{inequalities}. \\ $$
Commented by mr W last updated on 11/Mar/23

$${please}\:{explain}\:{a}\:{little}\:{more}! \\ $$$${the}\:{angles}\:{of}\:{the}\:{triangle}\:{should}\:{be} \\ $$$${integers},\:{e}.{g}.\:\mathrm{1}°+\mathrm{2}°+\mathrm{177}°\:{is}\:{such}\:{a} \\ $$$${triangle}. \\ $$
Commented by nikif99 last updated on 11/Mar/23

$${please}\:{let}\:{me}\:{examine}\:{it}\:{a}\:{little}\:{more}. \\ $$$${it}\:{seems}\:{there}\:{are}\:{errors}. \\ $$
Answered by mr W last updated on 11/Mar/23

$${an}\:{other}\:{method}\:{using}\:{generating} \\ $$$${function}: \\ $$$$\alpha+\beta+\gamma=\mathrm{180}° \\ $$$${with}\:\mathrm{1}°\leqslant\alpha\leqslant\beta\leqslant\gamma \\ $$$${let} \\ $$$$\alpha=\mathrm{1}+{p}\:{with}\:{p}\geqslant\mathrm{0} \\ $$$$\beta=\alpha+{q}=\mathrm{1}+{p}+{q}\:{with}\:{q}\geqslant\mathrm{0} \\ $$$$\gamma=\beta+{r}=\mathrm{1}+{p}+{q}+\gamma\:{with}\:{r}\geqslant\mathrm{0} \\ $$$$\left(\mathrm{1}+{p}\right)+\left(\mathrm{1}+{p}+{q}\right)+\left(\mathrm{1}+{p}+{q}+{r}\right)=\mathrm{180} \\ $$$$\Rightarrow\mathrm{3}+\mathrm{3}{p}+\mathrm{2}{q}+{r}=\mathrm{180}\:\:\:...\left({i}\right) \\ $$$${with}\:{p},{q},{r}\geqslant\mathrm{0} \\ $$$${number}\:{of}\:{solutions}\:{of}\:\left({i}\right)\:{is}\:{the} \\ $$$${coef}.\:{of}\:{term}\:{x}^{\mathrm{180}} \:{in}\:{the}\:{expansion}\:{of} \\ $$$${x}^{\mathrm{3}} \left(\mathrm{1}+{x}^{\mathrm{3}} +{x}^{\mathrm{6}} +...\right)\left(\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} +...\right)\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +...\right) \\ $$$$=\frac{{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}^{\mathrm{3}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}\right)} \\ $$$${which}\:{is}\:\mathrm{2700}. \\ $$$${therefore}\:{there}\:{are}\:\mathrm{2700}\:{triangles} \\ $$$${with}\:{integer}\:{angles}\:{in}\:{degrees}. \\ $$
Commented by mr W last updated on 11/Mar/23

