
Question Number 205733 by hardmath last updated on 28/Mar/24
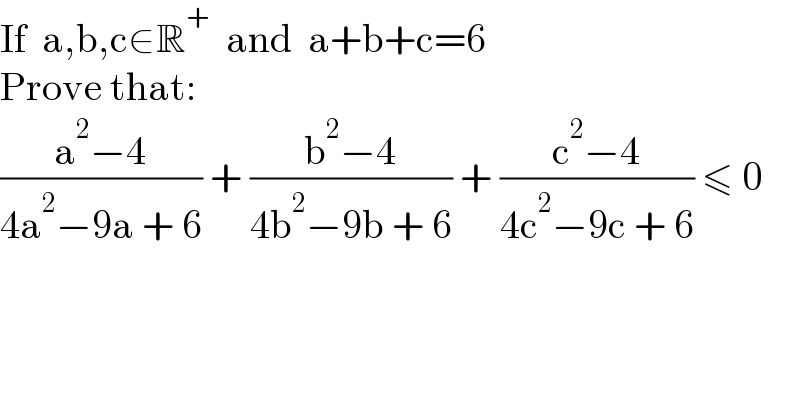
$$\mathrm{If}\:\:\mathrm{a},\mathrm{b},\mathrm{c}\in\mathbb{R}^{+} \:\:\mathrm{and}\:\:\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{6} \\ $$$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{4}}{\mathrm{4a}^{\mathrm{2}} −\mathrm{9a}\:+\:\mathrm{6}}\:+\:\frac{\mathrm{b}^{\mathrm{2}} −\mathrm{4}}{\mathrm{4b}^{\mathrm{2}} −\mathrm{9b}\:+\:\mathrm{6}}\:+\:\frac{\mathrm{c}^{\mathrm{2}} −\mathrm{4}}{\mathrm{4c}^{\mathrm{2}} −\mathrm{9c}\:+\:\mathrm{6}}\:\leqslant\:\mathrm{0} \\ $$
Answered by A5T last updated on 29/Mar/24
![4a^2 +16≥2(√(4×16a^2 ))=16a ⇒4a^2 +16−9a−10≥7a−10 ((a^2 −4=(a/7)(7a−10)+((10a)/7)−4)/(7a−10))=(a/7)+(((10a−28)/7)/(7a−10)) Question⇔Σ((a/7)+((10a−28)/(49a−70)))≤0 ⇔Σ((10a−28)/(49a−70))≤((−6)/7)⇔((10)/(49))×3−Σ((10a−28)/(49a−70))≥((72)/(49)) ⇔Σ(((672)/(343(7a−10))))≥((72)/(49))⇔((672)/(343))(Σ(1/((7a−10))))≥((72)/(49)) ⇔^? Σ(1/(7a−10))≥((72×343)/(49×672))=(3/4) (1/(7a−10))+(1/(7b−10))+(1/(7c−10))≥(9/(7(a+b+c)−30))=(9/(12))=(3/4) Since Σ(1/(7a−10))≥(3/4) as shown above,then original ineauality must be true[Equality when a=b=c=2]](Q205763.png)
$$\mathrm{4}{a}^{\mathrm{2}} +\mathrm{16}\geqslant\mathrm{2}\sqrt{\mathrm{4}×\mathrm{16}{a}^{\mathrm{2}} }=\mathrm{16}{a} \\ $$$$\Rightarrow\mathrm{4}{a}^{\mathrm{2}} +\mathrm{16}−\mathrm{9}{a}−\mathrm{10}\geqslant\mathrm{7}{a}−\mathrm{10} \\ $$$$\frac{{a}^{\mathrm{2}} −\mathrm{4}=\frac{{a}}{\mathrm{7}}\left(\mathrm{7}{a}−\mathrm{10}\right)+\frac{\mathrm{10}{a}}{\mathrm{7}}−\mathrm{4}}{\mathrm{7}{a}−\mathrm{10}}=\frac{{a}}{\mathrm{7}}+\frac{\frac{\mathrm{10}{a}−\mathrm{28}}{\mathrm{7}}}{\mathrm{7}{a}−\mathrm{10}} \\ $$$${Question}\Leftrightarrow\Sigma\left(\frac{{a}}{\mathrm{7}}+\frac{\mathrm{10}{a}−\mathrm{28}}{\mathrm{49}{a}−\mathrm{70}}\right)\leqslant\mathrm{0} \\ $$$$\Leftrightarrow\Sigma\frac{\mathrm{10}{a}−\mathrm{28}}{\mathrm{49}{a}−\mathrm{70}}\leqslant\frac{−\mathrm{6}}{\mathrm{7}}\Leftrightarrow\frac{\mathrm{10}}{\mathrm{49}}×\mathrm{3}−\Sigma\frac{\mathrm{10}{a}−\mathrm{28}}{\mathrm{49}{a}−\mathrm{70}}\geqslant\frac{\mathrm{72}}{\mathrm{49}} \\ $$$$\Leftrightarrow\Sigma\left(\frac{\mathrm{672}}{\mathrm{343}\left(\mathrm{7}{a}−\mathrm{10}\right)}\right)\geqslant\frac{\mathrm{72}}{\mathrm{49}}\Leftrightarrow\frac{\mathrm{672}}{\mathrm{343}}\left(\Sigma\frac{\mathrm{1}}{\left(\mathrm{7}{a}−\mathrm{10}\right)}\right)\geqslant\frac{\mathrm{72}}{\mathrm{49}} \\ $$$$\overset{?} {\Leftrightarrow}\Sigma\frac{\mathrm{1}}{\mathrm{7}{a}−\mathrm{10}}\geqslant\frac{\mathrm{72}×\mathrm{343}}{\mathrm{49}×\mathrm{672}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{7}{a}−\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{7}{b}−\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{7}{c}−\mathrm{10}}\geqslant\frac{\mathrm{9}}{\mathrm{7}\left({a}+{b}+{c}\right)−\mathrm{30}}=\frac{\mathrm{9}}{\mathrm{12}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${Since}\:\Sigma\frac{\mathrm{1}}{\mathrm{7}{a}−\mathrm{10}}\geqslant\frac{\mathrm{3}}{\mathrm{4}}\:{as}\:{shown}\:{above},{then}\:{original} \\ $$$${ineauality}\:{must}\:{be}\:{true}\left[{Equality}\:{when}\:{a}={b}={c}=\mathrm{2}\right] \\ $$
