
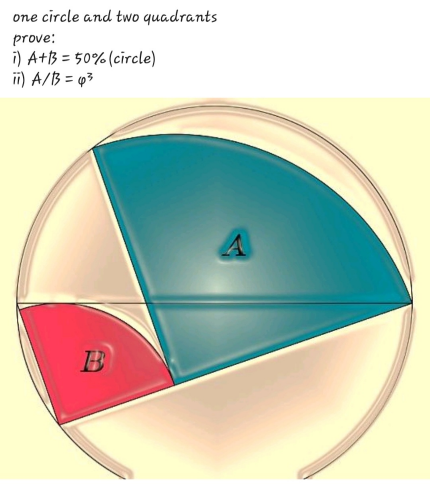
Question Number 191458 by Mingma last updated on 24/Apr/23
Answered by a.lgnaoui last updated on 26/Apr/23
![△ACD et △BCD semblablables AB tangdnte au quart cercle Rouge en D CD=R2 CD⊥AB ;BC=R1+R2 (R1 rayon du quart cercle vert. ABC triangle recrangle en C AB^2 =AC^2 +BC^2 (AB=diametre cercle jaune=2R) 4R^2 =AC^2 +(R1+R2)^2 (1) △ACD AC^2 =(AB−BCcos θ)^2 +(R2^2 ) =[2R−(R1+R2)cos θ)^2 ]+(R2)^2 θ=∡CBA (1)⇒ 4R^2 =[(2R−(R1+R2)cos 𝛉)^2 +(R2^2 )]+(R1+R2)^2 ⇒4R^2 =4R^2 +(R1+R2)^2 cos^2 θ −4R(R1+R2)cos θ)+(R2)^2 (R1+R2)^2 0=(R1+R2)^2 (1+cos^2 𝛉)−4R(R1+R2)cos θ+(R2)^2 0 =(R1^2 +R2^2 +2R1×R2)(1+cos^2 θ) −4R(R1+R2)cos θ +(R2^2 ) (2) △BCF CF^2 =(R1^2 )+(R2)^2 =2R^2 ⇒ (R1)^2 +R2^2 =2R^2 (3) ⇒0=2[(R^2 +(R1×R2)](1+cos^2 θ) −4R(R1+R2)cos θ+(R2)^2 2(R^2 +R1×R2)−4R(R1+R2)cos θ+R2^2 +2(R^2 +R1×R2)cos^2 θ =0 2R^2 (1+cos^2 𝛉) +2(R1×R2)(1+cos^2 𝛉) +R2^2 −4R(R1+R2)cos 𝛉=0 △BCD et △ EHB semblables sin θ=((R2)/(R1+R2))=((EH)/(R1))⇒EH=R1sin θ ⇒R2=R1sin𝛉 +R2sin 𝛉 [ R1=((R2(1−sin 𝛉))/(sin 𝛉)) ] ou [sin 𝛉=((R2)/(R1+R2)) △BIC BC=2Rcos θ⇒ ( R1+R2)=2Rcos θ [ cos 𝛉=((R1+R2)/(2R)) ] sin θ×cos θ=((R2)/(2R)) ⇒ [sin 2𝛉=((R2)/R) ] (4) Surface quart de cercle veet =(((πR1)^2 )/4) Celle du quart cercle Rouge=((π(R2)^2 )/4) (R1^2 )+(R2^2 )=2R^2 ⇒ S1+S2=((π(2R^2 ))/4)=((πR^2 )/2) Surface de qusrt ceecle vert et rouge =moitie de surface du cercle (4)⇒ ((Surfsce Vert)/(Surface Rouge))=(((R1)^2 )/((R2)^2 ))=((R^2 −(R2)^2 )/((Rsin 2𝛉)^2 )) =(1/(sin^2 2θ))−(((R2)/(Rsin 2θ)))^2 =(1/(sin^2 2θ))−1 =(1/(tan^2 2𝛉)) .to continoius....](Q191574.png)
$$\bigtriangleup\mathrm{ACD}\:\:\mathrm{et}\:\bigtriangleup\mathrm{BCD}\:\:\mathrm{semblablables} \\ $$$$\mathrm{AB}\:\mathrm{tangdnte}\:\mathrm{au}\:\mathrm{quart}\:\mathrm{cercle}\:\mathrm{Rouge}\:\mathrm{en}\:\mathrm{D} \\ $$$$\mathrm{CD}=\mathrm{R2}\:\:\:\mathrm{CD}\bot\mathrm{AB}\:\:;\mathrm{BC}=\mathrm{R1}+\mathrm{R2} \\ $$$$\left(\mathrm{R1}\:\mathrm{rayon}\:\mathrm{du}\:\:\mathrm{quart}\:\:\mathrm{cercle}\:\mathrm{vert}.\right. \\ $$$$\mathrm{ABC}\:\mathrm{triangle}\:\:\mathrm{recrangle}\:\mathrm{en}\:\mathrm{C} \\ $$$$\mathrm{AB}^{\mathrm{2}} =\mathrm{AC}^{\mathrm{2}} +\mathrm{BC}^{\mathrm{2}} \:\:\left(\mathrm{AB}=\mathrm{diametre}\:\mathrm{cercle}\:\mathrm{jaune}=\mathrm{2R}\right) \\ $$$$\mathrm{4R}^{\mathrm{2}} =\mathrm{AC}^{\mathrm{2}} +\left(\mathrm{R1}+\mathrm{R2}\right)^{\mathrm{2}} \:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\bigtriangleup\mathrm{ACD}\:\:\:\:\mathrm{AC}^{\mathrm{2}} =\left(\mathrm{AB}−\mathrm{BCcos}\:\theta\right)^{\mathrm{2}} +\left(\mathrm{R2}^{\mathrm{2}} \right) \\ $$$$\left.=\left[\mathrm{2R}−\left(\mathrm{R1}+\mathrm{R2}\right)\mathrm{cos}\:\theta\right)^{\mathrm{2}} \right]+\left(\mathrm{R2}\right)^{\mathrm{2}} \\ $$$$\theta=\measuredangle\mathrm{CBA} \\ $$$$\left(\mathrm{1}\right)\Rightarrow\:\mathrm{4}\boldsymbol{\mathrm{R}}^{\mathrm{2}} =\left[\left(\mathrm{2}\boldsymbol{\mathrm{R}}−\left(\boldsymbol{\mathrm{R}}\mathrm{1}+\boldsymbol{\mathrm{R}}\mathrm{2}\right)\mathrm{cos}\:\boldsymbol{\theta}\right)^{\mathrm{2}} +\left(\mathrm{R2}^{\mathrm{2}} \right)\right]+\left(\mathrm{R1}+\mathrm{R2}\right)^{\mathrm{2}} \\ $$$$\left.\Rightarrow\mathrm{4R}^{\mathrm{2}} =\mathrm{4R}^{\mathrm{2}} +\left(\mathrm{R1}+\mathrm{R2}\right)^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta\:−\mathrm{4R}\left(\mathrm{R1}+\mathrm{R2}\right)\mathrm{cos}\:\theta\right)+\left(\mathrm{R2}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{R1}+\mathrm{R2}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{0}=\left(\boldsymbol{\mathrm{R}}\mathrm{1}+\boldsymbol{\mathrm{R}}\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \boldsymbol{\theta}\right)−\mathrm{4}\boldsymbol{\mathrm{R}}\left(\boldsymbol{\mathrm{R}}\mathrm{1}+\boldsymbol{\mathrm{R}}\mathrm{2}\right)\mathrm{cos}\:\theta+\left(\boldsymbol{\mathrm{R}}\mathrm{2}\right)^{\mathrm{2}} \:\: \\ $$$$ \\ $$$$\:\:\mathrm{0}\:\:=\left(\mathrm{R1}^{\mathrm{2}} +\mathrm{R2}^{\mathrm{2}} +\mathrm{2R1}×\mathrm{R2}\right)\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:−\mathrm{4R}\left(\mathrm{R1}+\mathrm{R2}\right)\mathrm{cos}\:\theta\:\:+\left(\mathrm{R2}^{\mathrm{2}} \right)\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\bigtriangleup\mathrm{BCF}\:\:\:\mathrm{CF}^{\mathrm{2}} =\left(\mathrm{R1}^{\mathrm{2}} \right)+\left(\mathrm{R2}\right)^{\mathrm{2}} =\mathrm{2R}^{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\boldsymbol{\mathrm{R}}\mathrm{1}\right)^{\mathrm{2}} +\boldsymbol{\mathrm{R}}\mathrm{2}^{\mathrm{2}} =\mathrm{2}\boldsymbol{\mathrm{R}}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}\right) \\ $$$$ \\ $$$$\Rightarrow\mathrm{0}=\mathrm{2}\left[\left(\mathrm{R}^{\mathrm{2}} +\left(\mathrm{R1}×\mathrm{R2}\right)\right]\left(\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \theta\right)\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:−\mathrm{4R}\left(\mathrm{R1}+\mathrm{R2}\right)\mathrm{cos}\:\theta+\left(\mathrm{R2}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$$$\mathrm{2}\left(\mathrm{R}^{\mathrm{2}} +\mathrm{R1}×\mathrm{R2}\right)−\mathrm{4R}\left(\mathrm{R1}+\mathrm{R2}\right)\mathrm{cos}\:\theta+\mathrm{R2}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$$$+\mathrm{2}\left(\mathrm{R}^{\mathrm{2}} +\mathrm{R1}×\mathrm{R2}\right)\mathrm{cos}\:^{\mathrm{2}} \theta\:\:\:\:\:=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{2}\boldsymbol{\mathrm{R}}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \boldsymbol{\theta}\right)\:+\mathrm{2}\left(\boldsymbol{\mathrm{R}}\mathrm{1}×\boldsymbol{\mathrm{R}}\mathrm{2}\right)\left(\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \boldsymbol{\theta}\right) \\ $$$$+\boldsymbol{\mathrm{R}}\mathrm{2}^{\mathrm{2}} −\mathrm{4}\boldsymbol{\mathrm{R}}\left(\boldsymbol{\mathrm{R}}\mathrm{1}+\boldsymbol{\mathrm{R}}\mathrm{2}\right)\mathrm{cos}\:\boldsymbol{\theta}=\mathrm{0} \\ $$$$ \\ $$$$\bigtriangleup\mathrm{BCD}\:\:\:\mathrm{et}\:\bigtriangleup\:\mathrm{EHB}\:\:\:\mathrm{semblables} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{R2}}{\mathrm{R1}+\mathrm{R2}}=\frac{\mathrm{EH}}{\mathrm{R1}}\Rightarrow\mathrm{EH}=\mathrm{R1sin}\:\theta \\ $$$$\Rightarrow\boldsymbol{\mathrm{R}}\mathrm{2}=\boldsymbol{\mathrm{R}}\mathrm{1sin}\boldsymbol{\theta}\:+\boldsymbol{\mathrm{R}}\mathrm{2sin}\:\boldsymbol{\theta} \\ $$$$\:\:\:\:\:\left[\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{R}}\mathrm{1}=\frac{\boldsymbol{\mathrm{R}}\mathrm{2}\left(\mathrm{1}−\mathrm{sin}\:\boldsymbol{\theta}\right)}{\mathrm{sin}\:\boldsymbol{\theta}}\:\:\:\:\:\right]\:\:\:\:\mathrm{ou} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\mathrm{sin}\:\boldsymbol{\theta}=\frac{\boldsymbol{\mathrm{R}}\mathrm{2}}{\boldsymbol{\mathrm{R}}\mathrm{1}+\boldsymbol{\mathrm{R}}\mathrm{2}}\right. \\ $$$$\bigtriangleup\mathrm{BIC}\:\:\:\:\: \\ $$$$\mathrm{BC}=\mathrm{2Rcos}\:\theta\Rightarrow\:\left(\:\:\mathrm{R1}+\mathrm{R2}\right)=\mathrm{2Rcos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\:\mathrm{cos}\:\boldsymbol{\theta}=\frac{\boldsymbol{\mathrm{R}}\mathrm{1}+\boldsymbol{\mathrm{R}}\mathrm{2}}{\mathrm{2}\boldsymbol{\mathrm{R}}}\:\:\:\:\:\:\:\:\:\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sin}\:\theta×\mathrm{cos}\:\theta=\frac{\boldsymbol{\mathrm{R}}\mathrm{2}}{\mathrm{2}\boldsymbol{\mathrm{R}}}\:\:\:\:\: \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\mathrm{sin}\:\mathrm{2}\boldsymbol{\theta}=\frac{\mathrm{R2}}{\mathrm{R}}\:\:\:\right]\:\:\:\:\:\:\:\left(\mathrm{4}\right) \\ $$$$\:\:\mathrm{Surface}\:\:\mathrm{quart}\:\mathrm{de}\:\mathrm{cercle}\:\mathrm{veet}\:=\frac{\left(\pi\mathrm{R1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{Celle}\:\mathrm{du}\:\mathrm{quart}\:\mathrm{cercle}\:\mathrm{Rouge}=\frac{\pi\left(\mathrm{R2}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\left(\mathrm{R1}^{\mathrm{2}} \right)+\left(\mathrm{R2}^{\mathrm{2}} \right)=\mathrm{2R}^{\mathrm{2}} \:\:\:\:\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{S}}\mathrm{1}+\boldsymbol{\mathrm{S}}\mathrm{2}=\frac{\pi\left(\mathrm{2}\boldsymbol{\mathrm{R}}^{\mathrm{2}} \right)}{\mathrm{4}}=\frac{\pi\boldsymbol{\mathrm{R}}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{Surface}\:\boldsymbol{\mathrm{de}}\:\boldsymbol{\mathrm{qusrt}}\:\boldsymbol{\mathrm{ceecle}}\:\boldsymbol{\mathrm{vert}}\:\boldsymbol{\mathrm{et}}\:\boldsymbol{\mathrm{rouge}} \\ $$$$=\boldsymbol{\mathrm{moitie}}\:\boldsymbol{\mathrm{de}}\:\boldsymbol{\mathrm{surface}}\:\boldsymbol{\mathrm{du}}\:\boldsymbol{\mathrm{cercle}} \\ $$$$\:\:\:\:\:\left(\mathrm{4}\right)\Rightarrow \\ $$$$\:\:\:\frac{\boldsymbol{\mathrm{Surfsce}}\:\boldsymbol{\mathrm{Vert}}}{\boldsymbol{\mathrm{Surface}}\:\boldsymbol{\mathrm{Rouge}}}=\frac{\left(\boldsymbol{\mathrm{R}}\mathrm{1}\right)^{\mathrm{2}} }{\left(\boldsymbol{\mathrm{R}}\mathrm{2}\right)^{\mathrm{2}} }=\frac{\boldsymbol{\mathrm{R}}^{\mathrm{2}} −\left(\boldsymbol{\mathrm{R}}\mathrm{2}\right)^{\mathrm{2}} }{\left(\boldsymbol{\mathrm{R}}\mathrm{sin}\:\mathrm{2}\boldsymbol{\theta}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}\theta}−\left(\frac{\mathrm{R2}}{\mathrm{Rsin}\:\mathrm{2}\theta}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}\theta}−\mathrm{1} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{tan}\:^{\mathrm{2}} \mathrm{2}\boldsymbol{\theta}} \\ $$$$.\mathrm{to}\:\mathrm{continoius}.... \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 26/Apr/23

Answered by mr W last updated on 26/Apr/23

Commented by mr W last updated on 27/Apr/23

$${a}={radius}\:{of}\:{blue}\:{quater}\:{circle} \\ $$$${b}={radius}\:{of}\:{red}\:{quater}\:{circle} \\ $$$${R}={radius}\:{of}\:{big}\:{circle} \\ $$$$ \\ $$$$\frac{{a}+{b}}{{b}}=\frac{\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }}{\:{x}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\frac{{ab}^{\mathrm{2}} }{\:{a}+\mathrm{2}{b}} \\ $$$$ \\ $$$$\mathrm{2}{R}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\mathrm{sin}\:\mathrm{45}°}=\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\mathrm{2}{R}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}}=\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}+\frac{\pi{b}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{50\%}\:{circle}={A}+{B}\:\checkmark \\ $$$$ \\ $$$$\frac{\mathrm{2}{R}}{{a}+{b}}=\frac{\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }}{\:{a}} \\ $$$$\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}=\frac{{a}+{b}}{{a}}×\sqrt{{a}^{\mathrm{2}} +\frac{{ab}^{\mathrm{2}} }{{a}+\mathrm{2}{b}}} \\ $$$$\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)=\frac{\left({a}+{b}\right)^{\mathrm{4}} }{{a}\left({a}+\mathrm{2}{b}\right)} \\ $$$${a}^{\mathrm{4}} −\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −{b}^{\mathrm{4}} =\mathrm{0} \\ $$$$\left({a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{5}{b}^{\mathrm{4}} \\ $$$${a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} =\sqrt{\mathrm{5}}{b}^{\mathrm{2}} \: \\ $$$$\Rightarrow\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{2}+\sqrt{\mathrm{5}}=\varphi^{\mathrm{3}} =\frac{{A}}{{B}}\:\checkmark \\ $$
Commented by Mingma last updated on 27/Apr/23
Excellent, sir!
