
Question Number 191676 by ajfour last updated on 28/Apr/23
Commented by ajfour last updated on 28/Apr/23

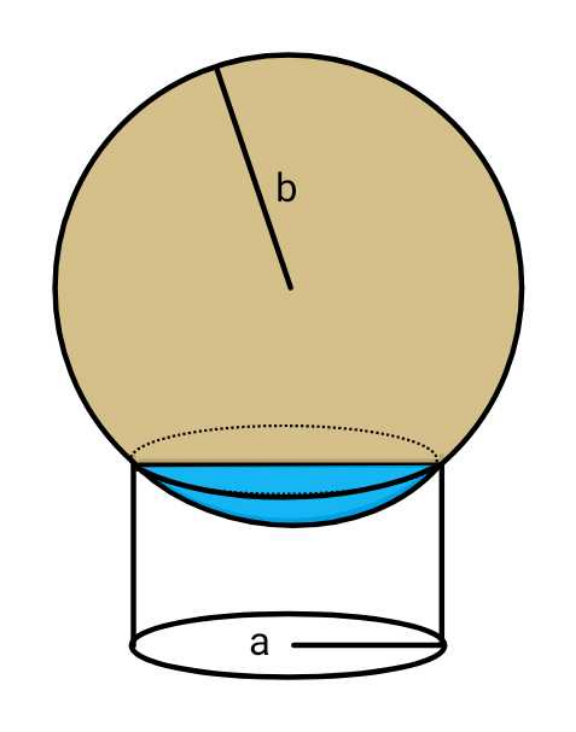
$${If}\:{first}\:{time}\:{dipped}\:{area}\:{of} \\ $$$${biscuit}\:{is}\:{A}_{\mathrm{1}} . \\ $$$${Find}\:\:{max}.\:{of}\:\frac{{A}_{\mathrm{2}} }{{A}_{\mathrm{1}} }.\:\: \\ $$$$\:{A}_{\mathrm{2}} \:{the}\:{area}\:{dipped}\:{the}\:{second}\: \\ $$$${time},\:{after}\:{A}_{\mathrm{1}} {is}\:{removed}. \\ $$
Commented by mr W last updated on 29/Apr/23

Answered by mr W last updated on 29/Apr/23

Commented by mr W last updated on 29/Apr/23
![sin φ=(a/r) a=r sin φ h=r cos φ A_1 =φr^2 −((r^2 sin 2φ)/2)=r^2 (φ−((sin 2φ)/2)) OA=(h/(cos θ))=((r cos φ)/(cos θ)) cos ϕ=((r^2 +((r^2 cos^2 φ)/(cos^2 θ))−a^2 )/(2r×((r cos φ)/(cos θ)))) ⇒ϕ=cos^(−1) [(((1−4 sin^2 φ) cos^2 θ+cos^2 φ)/(2 cos φ cos θ))] ((sin γ)/r)=((sin ϕ)/(2a)) ⇒γ=sin^(−1) (((sin ϕ)/(2 sin φ))) A_2 =(r^2 /2)(ϕ+θ−φ)+((rh [sin (φ−θ)−sin ϕ])/(2 cos θ)) A_2 =(r^2 /2)(ϕ+θ−φ)+((r^2 cos φ [sin (φ−θ)−sin ϕ])/(2 cos θ)) λ=(A_2 /A_1 )=((ϕ+θ−φ+((cos φ [sin (φ−θ)−sin ϕ])/(cos θ)))/(2φ−sin 2φ)) for λ_(max) : (dλ/dθ)=0 or (d/dθ){ϕ+θ−φ+((cos φ [sin (φ−θ)−sin ϕ])/(cos θ))}=0 this can only be nummerically solved. example: r=b=5, a=3 ⇒θ≈0.2261 or 12.955°](Q191684.png)
$$\mathrm{sin}\:\phi=\frac{{a}}{{r}} \\ $$$${a}={r}\:\mathrm{sin}\:\phi \\ $$$${h}={r}\:\mathrm{cos}\:\phi \\ $$$${A}_{\mathrm{1}} =\phi{r}^{\mathrm{2}} −\frac{{r}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\phi}{\mathrm{2}}={r}^{\mathrm{2}} \left(\phi−\frac{\mathrm{sin}\:\mathrm{2}\phi}{\mathrm{2}}\right) \\ $$$${OA}=\frac{{h}}{\mathrm{cos}\:\theta}=\frac{{r}\:\mathrm{cos}\:\phi}{\mathrm{cos}\:\theta} \\ $$$$\mathrm{cos}\:\varphi=\frac{{r}^{\mathrm{2}} +\frac{{r}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\phi}{\mathrm{cos}^{\mathrm{2}} \:\theta}−{a}^{\mathrm{2}} }{\mathrm{2}{r}×\frac{{r}\:\mathrm{cos}\:\phi}{\mathrm{cos}\:\theta}} \\ $$$$\Rightarrow\varphi=\mathrm{cos}^{−\mathrm{1}} \left[\frac{\left(\mathrm{1}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\phi\right)\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{cos}^{\mathrm{2}} \:\phi}{\mathrm{2}\:\mathrm{cos}\:\phi\:\mathrm{cos}\:\theta}\right] \\ $$$$\frac{\mathrm{sin}\:\gamma}{{r}}=\frac{\mathrm{sin}\:\varphi}{\mathrm{2}{a}} \\ $$$$\Rightarrow\gamma=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\varphi}{\mathrm{2}\:\mathrm{sin}\:\phi}\right) \\ $$$${A}_{\mathrm{2}} =\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\varphi+\theta−\phi\right)+\frac{{rh}\:\left[\mathrm{sin}\:\left(\phi−\theta\right)−\mathrm{sin}\:\varphi\right]}{\mathrm{2}\:\mathrm{cos}\:\theta} \\ $$$${A}_{\mathrm{2}} =\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\varphi+\theta−\phi\right)+\frac{{r}^{\mathrm{2}} \mathrm{cos}\:\phi\:\left[\mathrm{sin}\:\left(\phi−\theta\right)−\mathrm{sin}\:\varphi\right]}{\mathrm{2}\:\mathrm{cos}\:\theta} \\ $$$$\lambda=\frac{{A}_{\mathrm{2}} }{{A}_{\mathrm{1}} }=\frac{\varphi+\theta−\phi+\frac{\mathrm{cos}\:\phi\:\left[\mathrm{sin}\:\left(\phi−\theta\right)−\mathrm{sin}\:\varphi\right]}{\mathrm{cos}\:\theta}}{\mathrm{2}\phi−\mathrm{sin}\:\mathrm{2}\phi} \\ $$$${for}\:\lambda_{{max}} :\:\frac{{d}\lambda}{{d}\theta}=\mathrm{0}\:{or} \\ $$$$\frac{{d}}{{d}\theta}\left\{\varphi+\theta−\phi+\frac{\mathrm{cos}\:\phi\:\left[\mathrm{sin}\:\left(\phi−\theta\right)−\mathrm{sin}\:\varphi\right]}{\mathrm{cos}\:\theta}\right\}=\mathrm{0} \\ $$$${this}\:{can}\:{only}\:{be}\:{nummerically}\:{solved}. \\ $$$$ \\ $$$${example}: \\ $$$${r}={b}=\mathrm{5},\:{a}=\mathrm{3}\:\Rightarrow\theta\approx\mathrm{0}.\mathrm{2261}\:{or}\:\mathrm{12}.\mathrm{955}° \\ $$
Commented by mr W last updated on 29/Apr/23

Commented by ajfour last updated on 29/Apr/23

$${Thank}\:{you}\:{sir},\:{i}\:{shall}\:{follow}. \\ $$
Answered by a.lgnaoui last updated on 29/Apr/23
![Area A_1 (∅)=b^2 (2φ−sin ∅cos ∅) sin ∅=(a/(2b)) ∅=sin^(−1) ((a/(2b))) soit θ=2γ−φ A_2 (γ)=b^2 (2γ−sin γcos γ) (A_2 /A_1 )=((2𝛄−sin γcos γ)/(2∅−sin ∅cos ∅)) =(((θ+φ)−sin (((θ+∅)/2))cos( ((θ+∅)/2)))/(2∅−sin ∅cos ∅)) =((θ+∅−(1/2)sin (θ+∅))/(2∅−(a/(2b))×(√(1−(a^2 /(4b^2 )))))) =((θ+sin^(−1) ((a/(2b)))−(1/2)[(1/(2b))sin θ(√(4b^2 −a^2 )) +((bcos θ)/(2a))])/(2sin^(−1) ((a/(2b)))−(1/(4a))(√(4b^2 −a^2 ))))= (((θ+∅)−(1/4)((b/a)cos θ)+(((sin θ)/b))(√(4b^2 −a^2 )) ])/(2sin^(−1) ((a/(2b)))−(1/(4a))(√(4b^2 −a^2 )))) ((A2)/A_1 )=(1/2)[(((θ+φ)−(1/4)(((bcos θ)/a)+((sin θ(√(4b^2 −a^2 )))/b)))/(∅−((√(4b^2 −a^2 ))/(8a))))] (A_2 /A_1 ) max⇒∅=sin^(−1) ((a/(2b)))→(1/(8a))(√(4b^2 −a^2 )) ? { ((γ=((θ+∅)/2))),((∅: given with (a, b))) :} ....................?](Q191690.png)
$$\:\:\:\:\:\:\mathrm{Area}\:\:\boldsymbol{\mathrm{A}}_{\mathrm{1}} \left(\emptyset\right)=\mathrm{b}^{\mathrm{2}} \left(\mathrm{2}\phi−\mathrm{sin}\:\emptyset\mathrm{cos}\:\emptyset\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sin}\:\emptyset=\frac{\mathrm{a}}{\mathrm{2b}}\:\:\:\:\:\:\:\emptyset=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{2b}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{soit}\:\:\theta=\mathrm{2}\gamma−\phi\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{A}}_{\mathrm{2}} \left(\gamma\right)=\mathrm{b}^{\mathrm{2}} \left(\mathrm{2}\gamma−\mathrm{sin}\:\gamma\mathrm{cos}\:\gamma\right) \\ $$$$\:\:\:\:\:\:\:\:\:\frac{\boldsymbol{\mathrm{A}}_{\mathrm{2}} }{\boldsymbol{\mathrm{A}}_{\mathrm{1}} }=\frac{\mathrm{2}\boldsymbol{\gamma}−\mathrm{sin}\:\gamma\mathrm{cos}\:\gamma}{\mathrm{2}\emptyset−\mathrm{sin}\:\emptyset\mathrm{cos}\:\emptyset} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left(\theta+\phi\right)−\mathrm{sin}\:\left(\frac{\theta+\emptyset}{\mathrm{2}}\right)\mathrm{cos}\left(\:\frac{\theta+\emptyset}{\mathrm{2}}\right)}{\mathrm{2}\emptyset−\mathrm{sin}\:\emptyset\mathrm{cos}\:\emptyset} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\theta+\emptyset−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\left(\theta+\emptyset\right)}{\mathrm{2}\emptyset−\frac{\mathrm{a}}{\mathrm{2b}}×\sqrt{\mathrm{1}−\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{4b}^{\mathrm{2}} }}} \\ $$$$=\frac{\theta+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{2b}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2b}}\mathrm{sin}\:\theta\sqrt{\mathrm{4b}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \:}\:+\frac{\mathrm{bcos}\:\theta}{\mathrm{2a}}\right]}{\mathrm{2sin}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{2b}}\right)−\frac{\mathrm{1}}{\mathrm{4a}}\sqrt{\mathrm{4b}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }}= \\ $$$$\frac{\left.\left(\theta+\emptyset\right)−\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{b}}{\mathrm{a}}\mathrm{cos}\:\theta\right)+\left(\frac{\mathrm{sin}\:\theta}{\mathrm{b}}\right)\sqrt{\mathrm{4b}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \:}\:\right]}{\mathrm{2sin}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{2b}}\right)−\frac{\mathrm{1}}{\mathrm{4a}}\sqrt{\mathrm{4b}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }} \\ $$$$ \\ $$$$ \\ $$$$\frac{\boldsymbol{\mathrm{A}}\mathrm{2}}{\boldsymbol{\mathrm{A}}_{\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\left(\theta+\phi\right)−\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{bcos}\:\theta}{\mathrm{a}}+\frac{\mathrm{sin}\:\theta\sqrt{\mathrm{4b}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }}{\mathrm{b}}\right)}{\emptyset−\frac{\sqrt{\mathrm{4b}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }}{\mathrm{8a}}}\right] \\ $$$$ \\ $$$$\frac{\mathrm{A}_{\mathrm{2}} }{\mathrm{A}_{\mathrm{1}} }\:\:\mathrm{max}\Rightarrow\emptyset=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{2b}}\right)\rightarrow\frac{\mathrm{1}}{\mathrm{8a}}\sqrt{\mathrm{4b}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }\:\:\:? \\ $$$$\:\:\:\:\: \\ $$$$\begin{cases}{\gamma=\frac{\theta+\emptyset}{\mathrm{2}}}\\{\emptyset:\:\:\mathrm{given}\:\:\mathrm{with}\:\left(\mathrm{a},\:\:\mathrm{b}\right)}\end{cases} \\ $$$$....................? \\ $$
Commented by mr W last updated on 29/Apr/23

$${calculation}\:{of}\:{A}_{\mathrm{2}} \:{is}\:{totally}\:{wrong}! \\ $$$${shape}\:{of}\:{A}_{\mathrm{2}} \:{is}\:{not}\:{a}\:{segment}\:{of}\:{circle}! \\ $$
Commented by mr W last updated on 29/Apr/23

Commented by ajfour last updated on 29/Apr/23

$${Thanks}\:{sir},\:{i}\:{think}\:{i}\:{should}\:{not} \\ $$$${attempt}. \\ $$
Commented by ajfour last updated on 29/Apr/23

Commented by ajfour last updated on 29/Apr/23

$$\mathrm{sin}\:\alpha=\frac{{a}}{{b}} \\ $$$${A}_{\mathrm{1}} ={b}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} \frac{{a}}{{b}}−{a}\sqrt{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$${let}\:{C}\equiv\left(−{p},\:−\sqrt{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }\right)\equiv\left(−{p},\:−{q}\right) \\ $$$${E}\equiv\left(−{p}+{a}\mathrm{cos}\:\theta,\:−{q}+{a}\mathrm{sin}\:\theta\right) \\ $$$$−{p}+{a}\mathrm{cos}\:\theta={b}\mathrm{cos}\:\phi \\ $$$$−{q}+{a}\mathrm{sin}\:\theta={b}\mathrm{sin}\:\phi \\ $$$$\mathrm{2}\beta=\frac{\pi}{\mathrm{2}}+\phi−\alpha \\ $$$${A}_{\mathrm{2}} =\frac{\left({p}+{a}\right)\left(−{q}+{a}\mathrm{sin}\:\theta\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:+{b}^{\mathrm{2}} \beta−{b}^{\mathrm{2}} \mathrm{sin}\:\beta\mathrm{cos}\:\beta \\ $$$${now}\:\:{a}\mathrm{sin}\:\theta={b}\mathrm{sin}\:\phi+{q} \\ $$$$\Rightarrow\:\:\:\:\:{a}\mathrm{sin}\:\theta={q}+{b}\mathrm{sin}\:\left(\mathrm{2}\beta+\alpha−\frac{\pi}{\mathrm{2}}\right) \\ $$$${p}+{a}={a}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)−{b}\mathrm{cos}\:\phi \\ $$$$={a}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)−{b}\mathrm{cos}\:\left(\mathrm{2}\beta+\alpha−\frac{\pi}{\mathrm{2}}\right) \\ $$$$={a}+\sqrt{{a}^{\mathrm{2}} −\left\{{q}−{b}\mathrm{cos}\:\left(\mathrm{2}\beta+\alpha\right)\right\}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:−{b}\mathrm{sin}\:\left(\mathrm{2}\beta+\alpha\right) \\ $$$${hence}\:\:{A}_{\mathrm{2}} \left(\beta\right). \\ $$
