
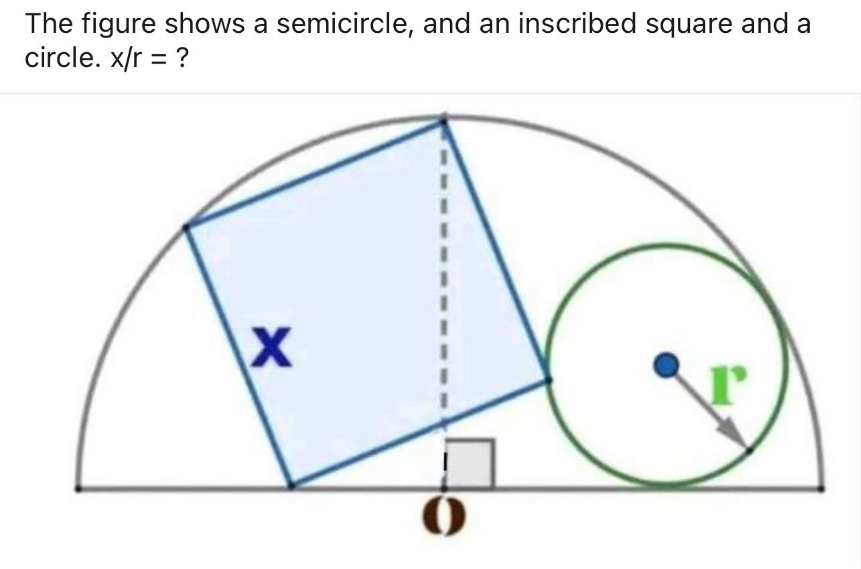
Question Number 194464 by Mingma last updated on 08/Jul/23
Answered by mr W last updated on 08/Jul/23
Commented by mr W last updated on 08/Jul/23
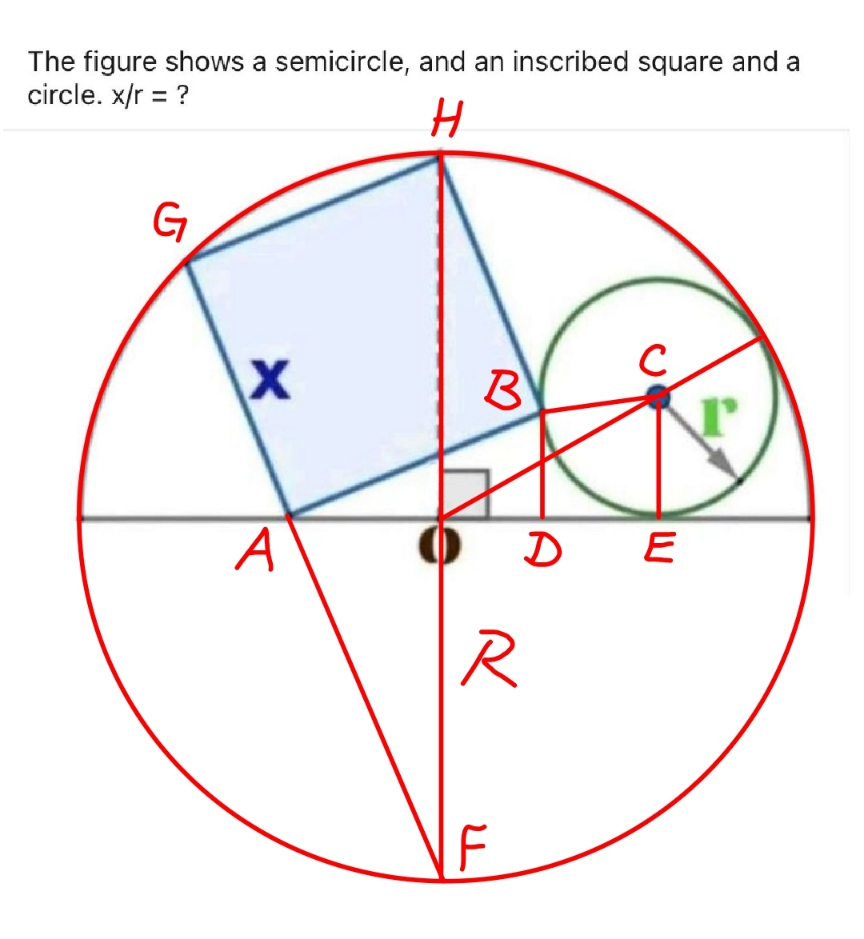
![R=radius of big circle GF=(√((2R)^2 −x^2 ))=(√(4R^2 −x^2 )) ((AF)/(OF))=((HF)/(GF)) ⇒(((√(4R^2 −x^2 ))−x)/R)=((2R)/( (√(4R^2 −x^2 )))) 4R^2 −x^2 −x(√(4R^2 −x^2 ))=2R^2 2R^2 −x^2 =x(√(4R^2 −x^2 )) 4R^4 −4R^2 x^2 +x^4 =4R^2 x^2 −x^4 x^4 −4R^2 x^2 +2R^4 =0 ⇒x^2 =(2−(√2))R^2 ⇒x=(√(2−(√2)))R OE=(√((R−r)^2 −r^2 ))=(√(R(R−2r))) ((AD)/(AB))=((GF)/(HF)) ⇒((AD)/x)=(((√(4R^2 −x^2 ))−x)/(2R)) ⇒AD=((x(√(4R^2 −x^2 ))−x^2 )/(2R))=((√2)−1)R ((BD)/(AB))=((GH)/(HF)) ⇒((BD)/x)=(x/(2R)) ⇒BD=(x^2 /(2R))=(((2−(√2))R)/2) ((AO)/(OF))=((GH)/(GF)) ⇒((AO)/x)=(x/( (√(4R^2 −x^2 )))) ⇒AO=(x^2 /( (√(4R^2 −x^2 ))))=((√2)−1)(√(2−(√2)))R DE=AO+OE−AD =((√2)−1)(√(2−(√2)))R+(√(R(R−2r)))−((√2)−1)R =((√2)−1)((√(2−(√2)))−1)R+(√(R(R−2r))) CE−BD=r−(((2−(√2))R)/2) [r−(((2−(√2))R)/2)]^2 +[((√2)−1)((√(2−(√2)))−1)R+(√(R(R−2r)))]^2 =r^2 (exact solution omited...) ⇒r≈0.387978R ⇒(x/R)≈((√(2−(√2)))/(0.387978))≈1.9727](Q194471.png)
$${R}={radius}\:{of}\:{big}\:{circle} \\ $$$${GF}=\sqrt{\left(\mathrm{2}{R}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} }=\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\frac{{AF}}{{OF}}=\frac{{HF}}{{GF}}\: \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }−{x}}{{R}}=\frac{\mathrm{2}{R}}{\:\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }} \\ $$$$\mathrm{4}{R}^{\mathrm{2}} −{x}^{\mathrm{2}} −{x}\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\mathrm{2}{R}^{\mathrm{2}} \\ $$$$\mathrm{2}{R}^{\mathrm{2}} −{x}^{\mathrm{2}} ={x}\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\mathrm{4}{R}^{\mathrm{4}} −\mathrm{4}{R}^{\mathrm{2}} {x}^{\mathrm{2}} +{x}^{\mathrm{4}} =\mathrm{4}{R}^{\mathrm{2}} {x}^{\mathrm{2}} −{x}^{\mathrm{4}} \\ $$$${x}^{\mathrm{4}} −\mathrm{4}{R}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}{R}^{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){R}^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}{R} \\ $$$${OE}=\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }=\sqrt{{R}\left({R}−\mathrm{2}{r}\right)} \\ $$$$\frac{{AD}}{{AB}}=\frac{{GF}}{{HF}} \\ $$$$\Rightarrow\frac{{AD}}{{x}}=\frac{\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }−{x}}{\mathrm{2}{R}} \\ $$$$\Rightarrow{AD}=\frac{{x}\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }−{x}^{\mathrm{2}} }{\mathrm{2}{R}}=\left(\sqrt{\mathrm{2}}−\mathrm{1}\right){R} \\ $$$$\frac{{BD}}{{AB}}=\frac{{GH}}{{HF}} \\ $$$$\Rightarrow\frac{{BD}}{{x}}=\frac{{x}}{\mathrm{2}{R}} \\ $$$$\Rightarrow{BD}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}{R}}=\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){R}}{\mathrm{2}} \\ $$$$\frac{{AO}}{{OF}}=\frac{{GH}}{{GF}} \\ $$$$\Rightarrow\frac{{AO}}{{x}}=\frac{{x}}{\:\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow{AO}=\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }}=\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}{R} \\ $$$${DE}={AO}+{OE}−{AD} \\ $$$$\:\:\:\:\:\:\:\:=\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}{R}+\sqrt{{R}\left({R}−\mathrm{2}{r}\right)}−\left(\sqrt{\mathrm{2}}−\mathrm{1}\right){R} \\ $$$$\:\:\:\:\:\:\:\:=\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\left(\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}−\mathrm{1}\right){R}+\sqrt{{R}\left({R}−\mathrm{2}{r}\right)} \\ $$$${CE}−{BD}={r}−\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){R}}{\mathrm{2}} \\ $$$$\left[{r}−\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){R}}{\mathrm{2}}\right]^{\mathrm{2}} +\left[\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\left(\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}−\mathrm{1}\right){R}+\sqrt{{R}\left({R}−\mathrm{2}{r}\right)}\right]^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left({exact}\:{solution}\:{omited}...\right) \\ $$$$\Rightarrow{r}\approx\mathrm{0}.\mathrm{387978}{R} \\ $$$$\Rightarrow\frac{{x}}{{R}}\approx\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}{\mathrm{0}.\mathrm{387978}}\approx\mathrm{1}.\mathrm{9727} \\ $$
Commented by Mingma last updated on 08/Jul/23
Very great solution, sir!
