Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 195470 by Shlock last updated on 03/Aug/23

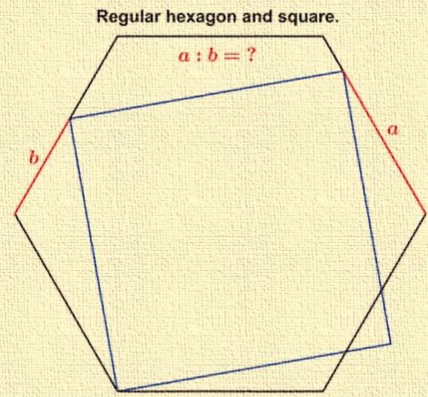
Answered by mr W last updated on 03/Aug/23

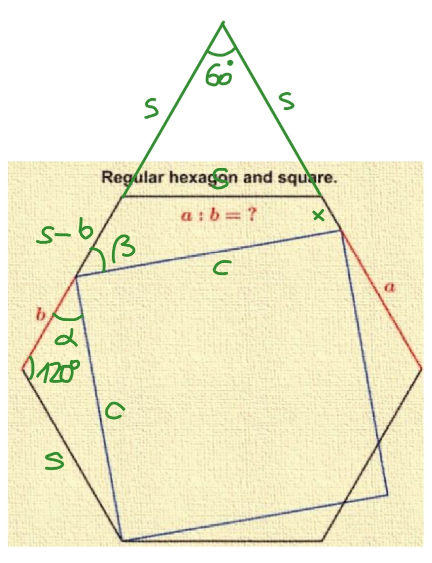
Commented by mr W last updated on 03/Aug/23

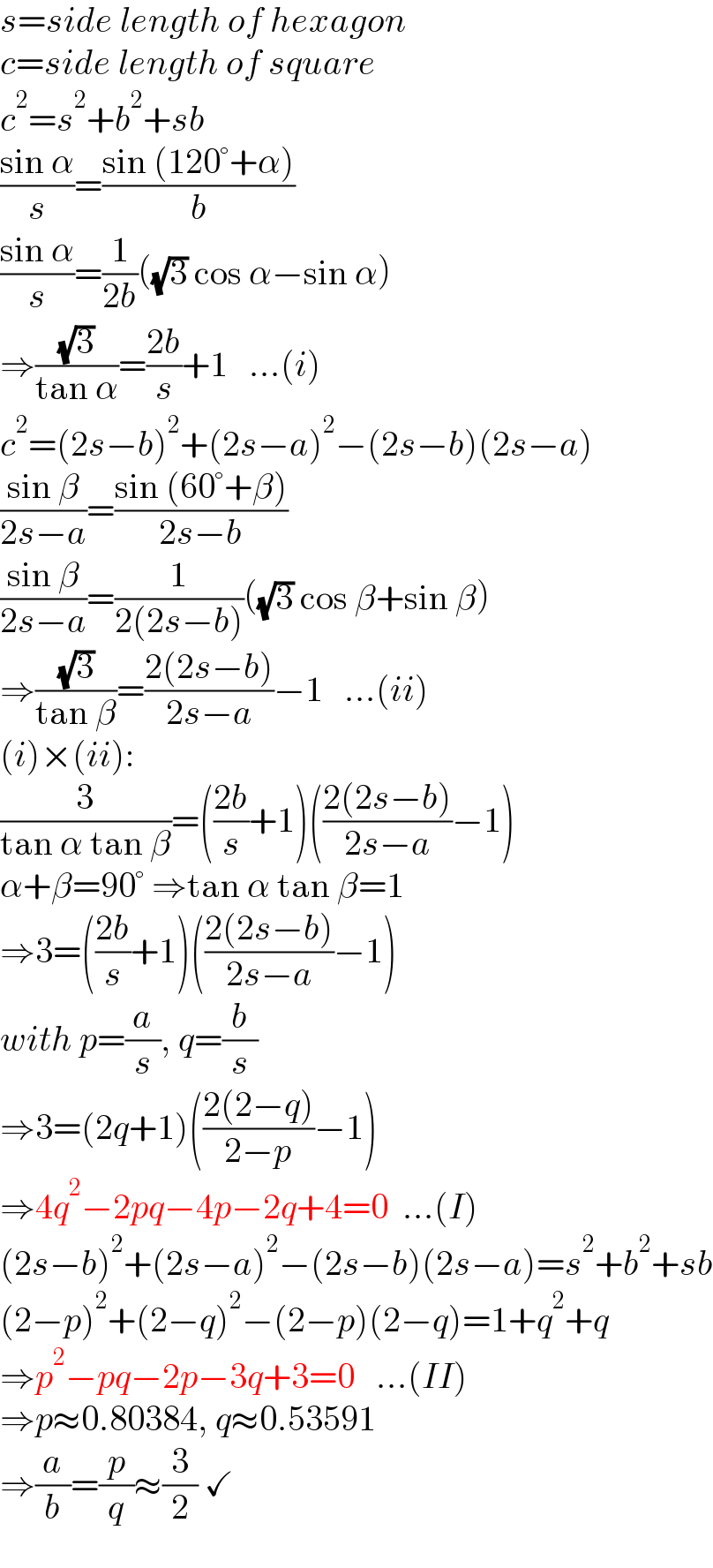
s=side length of hexagon c=side length of square c^2 =s^2 +b^2 +sb ((sin α)/s)=((sin (120°+α))/b) ((sin α)/s)=(1/(2b))((√3) cos α−sin α) ⇒((√3)/(tan α))=((2b)/s)+1 ...(i) c^2 =(2s−b)^2 +(2s−a)^2 −(2s−b)(2s−a) ((sin β)/(2s−a))=((sin (60°+β))/(2s−b)) ((sin β)/(2s−a))=(1/(2(2s−b)))((√3) cos β+sin β) ⇒((√3)/(tan β))=((2(2s−b))/(2s−a))−1 ...(ii) (i)×(ii): (3/(tan α tan β))=(((2b)/s)+1)(((2(2s−b))/(2s−a))−1) α+β=90° ⇒tan α tan β=1 ⇒3=(((2b)/s)+1)(((2(2s−b))/(2s−a))−1) with p=(a/s), q=(b/s) ⇒3=(2q+1)(((2(2−q))/(2−p))−1) ⇒4q^2 −2pq−4p−2q+4=0 ...(I) (2s−b)^2 +(2s−a)^2 −(2s−b)(2s−a)=s^2 +b^2 +sb (2−p)^2 +(2−q)^2 −(2−p)(2−q)=1+q^2 +q ⇒p^2 −pq−2p−3q+3=0 ...(II) ⇒p≈0.80384, q≈0.53591 ⇒(a/b)=(p/q)≈(3/2) ✓

$${s}={side}\:{length}\:{of}\:{hexagon} \\ $$$${c}={side}\:{length}\:{of}\:{square} \\ $$$${c}^{\mathrm{2}} ={s}^{\mathrm{2}} +{b}^{\mathrm{2}} +{sb} \\ $$$$\frac{\mathrm{sin}\:\alpha}{{s}}=\frac{\mathrm{sin}\:\left(\mathrm{120}°+\alpha\right)}{{b}} \\ $$$$\frac{\mathrm{sin}\:\alpha}{{s}}=\frac{\mathrm{1}}{\mathrm{2}{b}}\left(\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha\right) \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\alpha}=\frac{\mathrm{2}{b}}{{s}}+\mathrm{1}\:\:\:...\left({i}\right) \\ $$$${c}^{\mathrm{2}} =\left(\mathrm{2}{s}−{b}\right)^{\mathrm{2}} +\left(\mathrm{2}{s}−{a}\right)^{\mathrm{2}} −\left(\mathrm{2}{s}−{b}\right)\left(\mathrm{2}{s}−{a}\right) \\ $$$$\frac{\mathrm{sin}\:\beta}{\mathrm{2}{s}−{a}}=\frac{\mathrm{sin}\:\left(\mathrm{60}°+\beta\right)}{\mathrm{2}{s}−{b}} \\ $$$$\frac{\mathrm{sin}\:\beta}{\mathrm{2}{s}−{a}}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{s}−{b}\right)}\left(\sqrt{\mathrm{3}}\:\mathrm{cos}\:\beta+\mathrm{sin}\:\beta\right) \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\beta}=\frac{\mathrm{2}\left(\mathrm{2}{s}−{b}\right)}{\mathrm{2}{s}−{a}}−\mathrm{1}\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right): \\ $$$$\frac{\mathrm{3}}{\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta}=\left(\frac{\mathrm{2}{b}}{{s}}+\mathrm{1}\right)\left(\frac{\mathrm{2}\left(\mathrm{2}{s}−{b}\right)}{\mathrm{2}{s}−{a}}−\mathrm{1}\right) \\ $$$$\alpha+\beta=\mathrm{90}°\:\Rightarrow\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta=\mathrm{1} \\ $$$$\Rightarrow\mathrm{3}=\left(\frac{\mathrm{2}{b}}{{s}}+\mathrm{1}\right)\left(\frac{\mathrm{2}\left(\mathrm{2}{s}−{b}\right)}{\mathrm{2}{s}−{a}}−\mathrm{1}\right) \\ $$$${with}\:{p}=\frac{{a}}{{s}},\:{q}=\frac{{b}}{{s}} \\ $$$$\Rightarrow\mathrm{3}=\left(\mathrm{2}{q}+\mathrm{1}\right)\left(\frac{\mathrm{2}\left(\mathrm{2}−{q}\right)}{\mathrm{2}−{p}}−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{4}{q}^{\mathrm{2}} −\mathrm{2}{pq}−\mathrm{4}{p}−\mathrm{2}{q}+\mathrm{4}=\mathrm{0}\:\:...\left({I}\right) \\ $$$$\left(\mathrm{2}{s}−{b}\right)^{\mathrm{2}} +\left(\mathrm{2}{s}−{a}\right)^{\mathrm{2}} −\left(\mathrm{2}{s}−{b}\right)\left(\mathrm{2}{s}−{a}\right)={s}^{\mathrm{2}} +{b}^{\mathrm{2}} +{sb} \\ $$$$\left(\mathrm{2}−{p}\right)^{\mathrm{2}} +\left(\mathrm{2}−{q}\right)^{\mathrm{2}} −\left(\mathrm{2}−{p}\right)\left(\mathrm{2}−{q}\right)=\mathrm{1}+{q}^{\mathrm{2}} +{q} \\ $$$$\Rightarrow{p}^{\mathrm{2}} −{pq}−\mathrm{2}{p}−\mathrm{3}{q}+\mathrm{3}=\mathrm{0}\:\:\:...\left({II}\right) \\ $$$$\Rightarrow{p}\approx\mathrm{0}.\mathrm{80384},\:{q}\approx\mathrm{0}.\mathrm{53591} \\ $$$$\Rightarrow\frac{{a}}{{b}}=\frac{{p}}{{q}}\approx\frac{\mathrm{3}}{\mathrm{2}}\:\checkmark \\ $$

Commented by Shlock last updated on 03/Aug/23

This is a great solution, sir! Thanks!

Answered by mr W last updated on 03/Aug/23

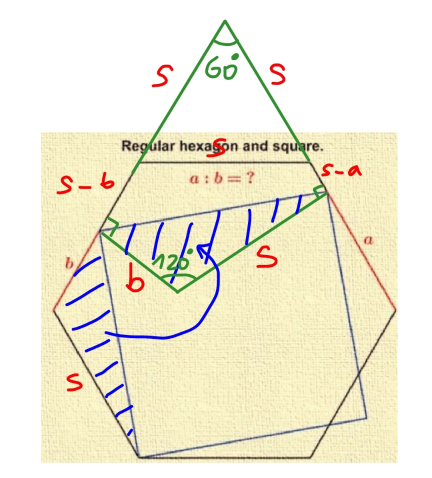
Commented by mr W last updated on 03/Aug/23

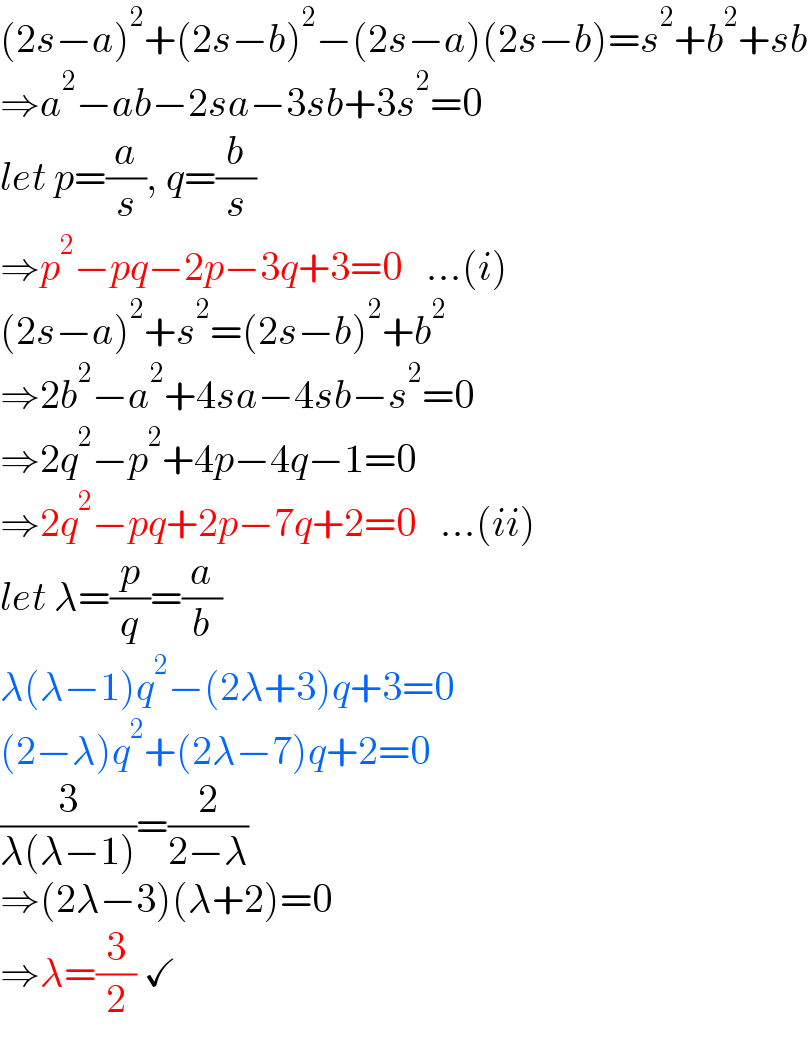
(2s−a)^2 +(2s−b)^2 −(2s−a)(2s−b)=s^2 +b^2 +sb ⇒a^2 −ab−2sa−3sb+3s^2 =0 let p=(a/s), q=(b/s) ⇒p^2 −pq−2p−3q+3=0 ...(i) (2s−a)^2 +s^2 =(2s−b)^2 +b^2 ⇒2b^2 −a^2 +4sa−4sb−s^2 =0 ⇒2q^2 −p^2 +4p−4q−1=0 ⇒2q^2 −pq+2p−7q+2=0 ...(ii) let λ=(p/q)=(a/b) λ(λ−1)q^2 −(2λ+3)q+3=0 (2−λ)q^2 +(2λ−7)q+2=0 (3/(λ(λ−1)))=(2/(2−λ)) ⇒(2λ−3)(λ+2)=0 ⇒λ=(3/2) ✓

$$\left(\mathrm{2}{s}−{a}\right)^{\mathrm{2}} +\left(\mathrm{2}{s}−{b}\right)^{\mathrm{2}} −\left(\mathrm{2}{s}−{a}\right)\left(\mathrm{2}{s}−{b}\right)={s}^{\mathrm{2}} +{b}^{\mathrm{2}} +{sb} \\ $$$$\Rightarrow{a}^{\mathrm{2}} −{ab}−\mathrm{2}{sa}−\mathrm{3}{sb}+\mathrm{3}{s}^{\mathrm{2}} =\mathrm{0} \\ $$$${let}\:{p}=\frac{{a}}{{s}},\:{q}=\frac{{b}}{{s}} \\ $$$$\Rightarrow{p}^{\mathrm{2}} −{pq}−\mathrm{2}{p}−\mathrm{3}{q}+\mathrm{3}=\mathrm{0}\:\:\:...\left({i}\right) \\ $$$$\left(\mathrm{2}{s}−{a}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} =\left(\mathrm{2}{s}−{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{b}^{\mathrm{2}} −{a}^{\mathrm{2}} +\mathrm{4}{sa}−\mathrm{4}{sb}−{s}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{q}^{\mathrm{2}} −{p}^{\mathrm{2}} +\mathrm{4}{p}−\mathrm{4}{q}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{q}^{\mathrm{2}} −{pq}+\mathrm{2}{p}−\mathrm{7}{q}+\mathrm{2}=\mathrm{0}\:\:\:...\left({ii}\right) \\ $$$${let}\:\lambda=\frac{{p}}{{q}}=\frac{{a}}{{b}} \\ $$$$\lambda\left(\lambda−\mathrm{1}\right){q}^{\mathrm{2}} −\left(\mathrm{2}\lambda+\mathrm{3}\right){q}+\mathrm{3}=\mathrm{0} \\ $$$$\left(\mathrm{2}−\lambda\right){q}^{\mathrm{2}} +\left(\mathrm{2}\lambda−\mathrm{7}\right){q}+\mathrm{2}=\mathrm{0} \\ $$$$\frac{\mathrm{3}}{\lambda\left(\lambda−\mathrm{1}\right)}=\frac{\mathrm{2}}{\mathrm{2}−\lambda} \\ $$$$\Rightarrow\left(\mathrm{2}\lambda−\mathrm{3}\right)\left(\lambda+\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{3}}{\mathrm{2}}\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com