
Previous in Relation and Functions Next in Relation and Functions
Question Number 201848 by cortano12 last updated on 14/Dec/23

Answered by mr W last updated on 14/Dec/23
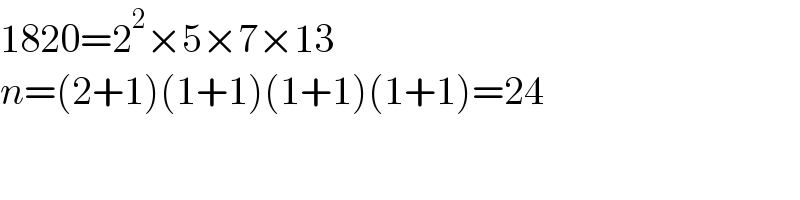
$$\mathrm{1820}=\mathrm{2}^{\mathrm{2}} ×\mathrm{5}×\mathrm{7}×\mathrm{13} \\ $$$${n}=\left(\mathrm{2}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}\right)=\mathrm{24} \\ $$
Commented by cortano12 last updated on 14/Dec/23
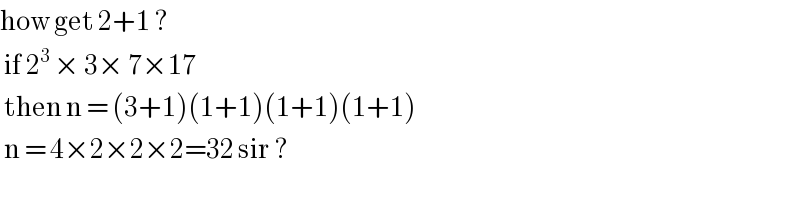
$$\mathrm{how}\:\mathrm{get}\:\mathrm{2}+\mathrm{1}\:?\: \\ $$$$\:\mathrm{if}\:\mathrm{2}^{\mathrm{3}} \:×\:\mathrm{3}×\:\mathrm{7}×\mathrm{17}\: \\ $$$$\:\mathrm{then}\:\mathrm{n}\:=\:\left(\mathrm{3}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}\right) \\ $$$$\:\mathrm{n}\:=\:\mathrm{4}×\mathrm{2}×\mathrm{2}×\mathrm{2}=\mathrm{32}\:\mathrm{sir}\:? \\ $$
Commented by mr W last updated on 14/Dec/23
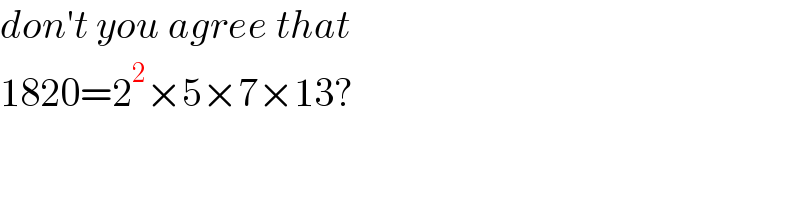
$${don}'{t}\:{you}\:{agree}\:{that} \\ $$$$\mathrm{1820}=\mathrm{2}^{\mathrm{2}} ×\mathrm{5}×\mathrm{7}×\mathrm{13}? \\ $$
Commented by cortano12 last updated on 14/Dec/23
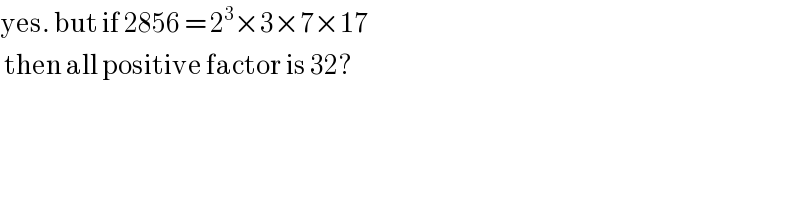
$$\mathrm{yes}.\:\mathrm{but}\:\mathrm{if}\:\mathrm{2856}\:=\:\mathrm{2}^{\mathrm{3}} ×\mathrm{3}×\mathrm{7}×\mathrm{17} \\ $$$$\:\mathrm{then}\:\mathrm{all}\:\mathrm{positive}\:\mathrm{factor}\:\mathrm{is}\:\mathrm{32}? \\ $$
Commented by cortano12 last updated on 14/Dec/23

$$\mathrm{what}\:\mathrm{this}\:\mathrm{formula}? \\ $$
Commented by mr W last updated on 14/Dec/23
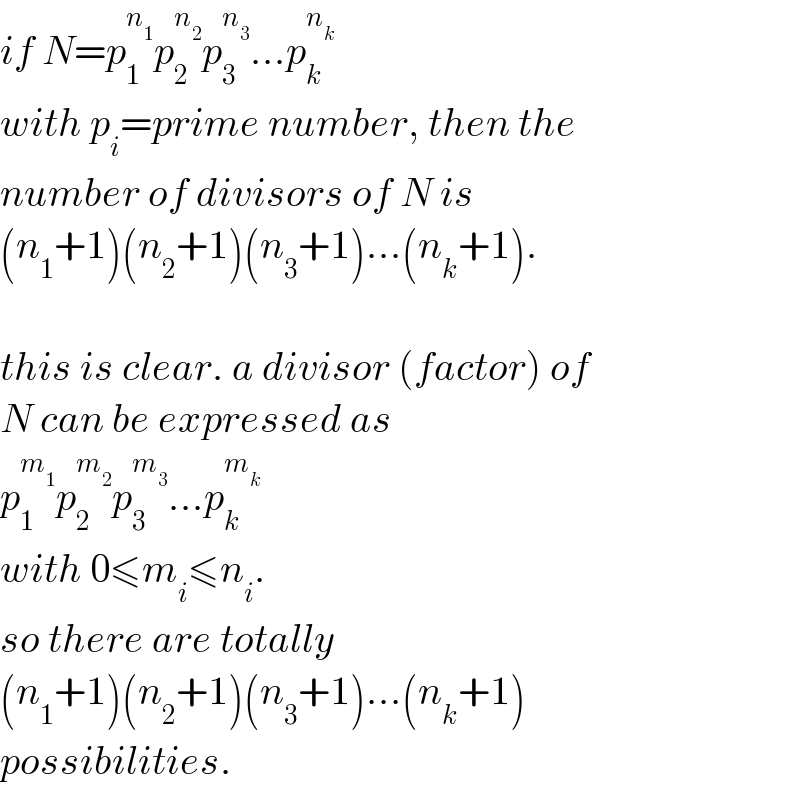
$${if}\:{N}={p}_{\mathrm{1}} ^{{n}_{\mathrm{1}} } {p}_{\mathrm{2}} ^{{n}_{\mathrm{2}} } {p}_{\mathrm{3}} ^{{n}_{\mathrm{3}} } ...{p}_{{k}} ^{{n}_{{k}} } \\ $$$${with}\:{p}_{{i}} ={prime}\:{number},\:{then}\:{the} \\ $$$${number}\:{of}\:{divisors}\:{of}\:{N}\:{is} \\ $$$$\left({n}_{\mathrm{1}} +\mathrm{1}\right)\left({n}_{\mathrm{2}} +\mathrm{1}\right)\left({n}_{\mathrm{3}} +\mathrm{1}\right)...\left({n}_{{k}} +\mathrm{1}\right). \\ $$$$ \\ $$$${this}\:{is}\:{clear}.\:{a}\:{divisor}\:\left({factor}\right)\:{of} \\ $$$${N}\:{can}\:{be}\:{expressed}\:{as} \\ $$$${p}_{\mathrm{1}} ^{{m}_{\mathrm{1}} } {p}_{\mathrm{2}} ^{{m}_{\mathrm{2}} } {p}_{\mathrm{3}} ^{{m}_{\mathrm{3}} } ...{p}_{{k}} ^{{m}_{{k}} } \\ $$$${with}\:\mathrm{0}\leqslant{m}_{{i}} \leqslant{n}_{{i}} . \\ $$$${so}\:{there}\:{are}\:{totally} \\ $$$$\left({n}_{\mathrm{1}} +\mathrm{1}\right)\left({n}_{\mathrm{2}} +\mathrm{1}\right)\left({n}_{\mathrm{3}} +\mathrm{1}\right)...\left({n}_{{k}} +\mathrm{1}\right) \\ $$$${possibilities}. \\ $$
