Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 202374 by Calculusboy last updated on 25/Dec/23

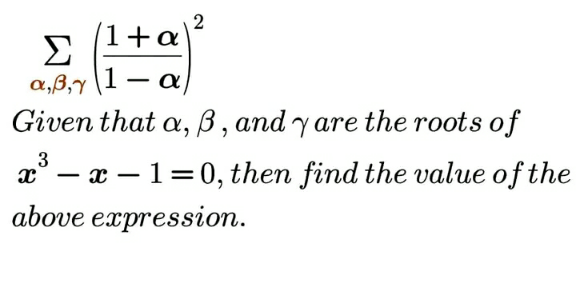
Commented by Frix last updated on 25/Dec/23

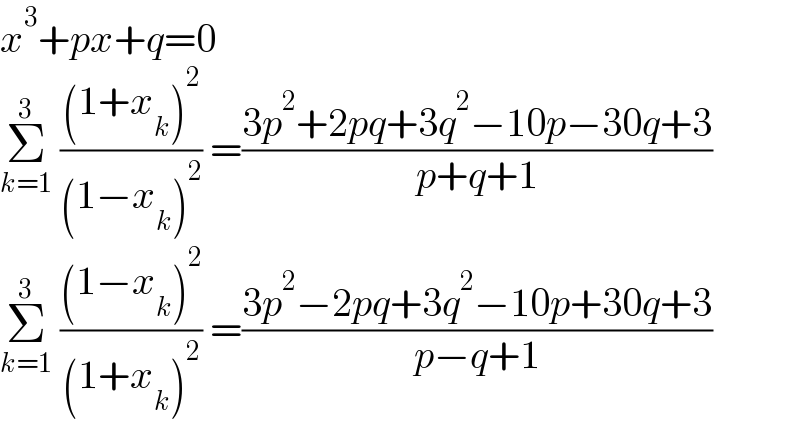
x^3 +px+q=0 Σ_(k=1) ^3 (((1+x_k )^2 )/((1−x_k )^2 )) =((3p^2 +2pq+3q^2 −10p−30q+3)/(p+q+1)) Σ_(k=1) ^3 (((1−x_k )^2 )/((1+x_k )^2 )) =((3p^2 −2pq+3q^2 −10p+30q+3)/(p−q+1))

$${x}^{\mathrm{3}} +{px}+{q}=\mathrm{0} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{3}} {\sum}}\:\frac{\left(\mathrm{1}+{x}_{{k}} \right)^{\mathrm{2}} }{\left(\mathrm{1}−{x}_{{k}} \right)^{\mathrm{2}} }\:=\frac{\mathrm{3}{p}^{\mathrm{2}} +\mathrm{2}{pq}+\mathrm{3}{q}^{\mathrm{2}} −\mathrm{10}{p}−\mathrm{30}{q}+\mathrm{3}}{{p}+{q}+\mathrm{1}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{3}} {\sum}}\:\frac{\left(\mathrm{1}−{x}_{{k}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+{x}_{{k}} \right)^{\mathrm{2}} }\:=\frac{\mathrm{3}{p}^{\mathrm{2}} −\mathrm{2}{pq}+\mathrm{3}{q}^{\mathrm{2}} −\mathrm{10}{p}+\mathrm{30}{q}+\mathrm{3}}{{p}−{q}+\mathrm{1}} \\ $$

Commented by Calculusboy last updated on 26/Dec/23

nice solution

$$\boldsymbol{{nice}}\:\boldsymbol{{solution}} \\ $$

Answered by aleks041103 last updated on 25/Dec/23

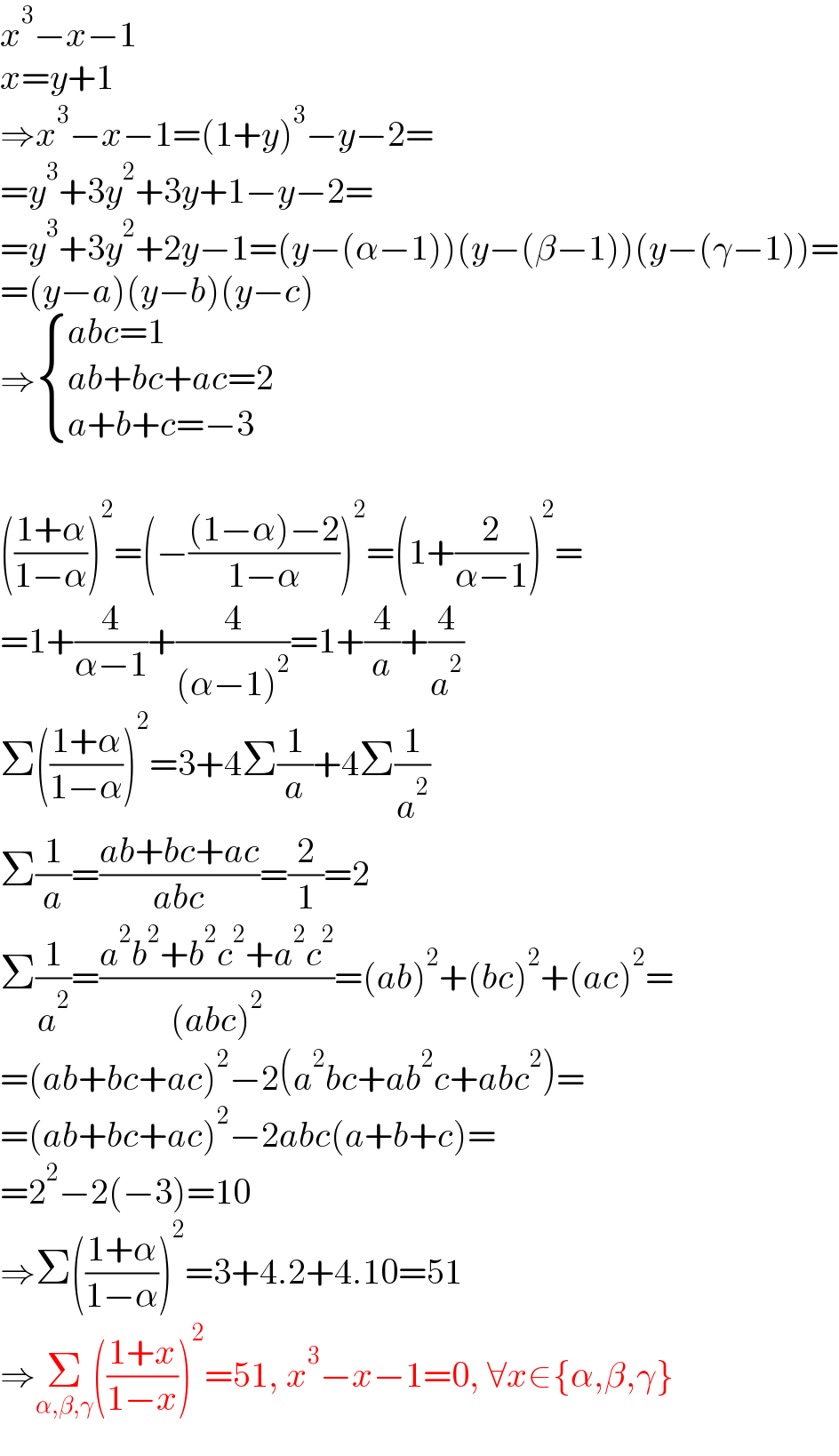
x^3 −x−1 x=y+1 ⇒x^3 −x−1=(1+y)^3 −y−2= =y^3 +3y^2 +3y+1−y−2= =y^3 +3y^2 +2y−1=(y−(α−1))(y−(β−1))(y−(γ−1))= =(y−a)(y−b)(y−c) ⇒ { ((abc=1)),((ab+bc+ac=2)),((a+b+c=−3)) :} (((1+α)/(1−α)))^2 =(−(((1−α)−2)/(1−α)))^2 =(1+(2/(α−1)))^2 = =1+(4/(α−1))+(4/((α−1)^2 ))=1+(4/a)+(4/a^2 ) Σ(((1+α)/(1−α)))^2 =3+4Σ(1/a)+4Σ(1/a^2 ) Σ(1/a)=((ab+bc+ac)/(abc))=(2/1)=2 Σ(1/a^2 )=((a^2 b^2 +b^2 c^2 +a^2 c^2 )/((abc)^2 ))=(ab)^2 +(bc)^2 +(ac)^2 = =(ab+bc+ac)^2 −2(a^2 bc+ab^2 c+abc^2 )= =(ab+bc+ac)^2 −2abc(a+b+c)= =2^2 −2(−3)=10 ⇒Σ(((1+α)/(1−α)))^2 =3+4.2+4.10=51 ⇒Σ_(α,β,γ) (((1+x)/(1−x)))^2 =51, x^3 −x−1=0, ∀x∈{α,β,γ}

$${x}^{\mathrm{3}} −{x}−\mathrm{1} \\ $$$${x}={y}+\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{3}} −{x}−\mathrm{1}=\left(\mathrm{1}+{y}\right)^{\mathrm{3}} −{y}−\mathrm{2}= \\ $$$$={y}^{\mathrm{3}} +\mathrm{3}{y}^{\mathrm{2}} +\mathrm{3}{y}+\mathrm{1}−{y}−\mathrm{2}= \\ $$$$={y}^{\mathrm{3}} +\mathrm{3}{y}^{\mathrm{2}} +\mathrm{2}{y}−\mathrm{1}=\left({y}−\left(\alpha−\mathrm{1}\right)\right)\left({y}−\left(\beta−\mathrm{1}\right)\right)\left({y}−\left(\gamma−\mathrm{1}\right)\right)= \\ $$$$=\left({y}−{a}\right)\left({y}−{b}\right)\left({y}−{c}\right) \\ $$$$\Rightarrow\begin{cases}{{abc}=\mathrm{1}}\\{{ab}+{bc}+{ac}=\mathrm{2}}\\{{a}+{b}+{c}=−\mathrm{3}}\end{cases} \\ $$$$ \\ $$$$\left(\frac{\mathrm{1}+\alpha}{\mathrm{1}−\alpha}\right)^{\mathrm{2}} =\left(−\frac{\left(\mathrm{1}−\alpha\right)−\mathrm{2}}{\mathrm{1}−\alpha}\right)^{\mathrm{2}} =\left(\mathrm{1}+\frac{\mathrm{2}}{\alpha−\mathrm{1}}\right)^{\mathrm{2}} = \\ $$$$=\mathrm{1}+\frac{\mathrm{4}}{\alpha−\mathrm{1}}+\frac{\mathrm{4}}{\left(\alpha−\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{1}+\frac{\mathrm{4}}{{a}}+\frac{\mathrm{4}}{{a}^{\mathrm{2}} } \\ $$$$\Sigma\left(\frac{\mathrm{1}+\alpha}{\mathrm{1}−\alpha}\right)^{\mathrm{2}} =\mathrm{3}+\mathrm{4}\Sigma\frac{\mathrm{1}}{{a}}+\mathrm{4}\Sigma\frac{\mathrm{1}}{{a}^{\mathrm{2}} } \\ $$$$\Sigma\frac{\mathrm{1}}{{a}}=\frac{{ab}+{bc}+{ac}}{{abc}}=\frac{\mathrm{2}}{\mathrm{1}}=\mathrm{2} \\ $$$$\Sigma\frac{\mathrm{1}}{{a}^{\mathrm{2}} }=\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} }{\left({abc}\right)^{\mathrm{2}} }=\left({ab}\right)^{\mathrm{2}} +\left({bc}\right)^{\mathrm{2}} +\left({ac}\right)^{\mathrm{2}} = \\ $$$$=\left({ab}+{bc}+{ac}\right)^{\mathrm{2}} −\mathrm{2}\left({a}^{\mathrm{2}} {bc}+{ab}^{\mathrm{2}} {c}+{abc}^{\mathrm{2}} \right)= \\ $$$$=\left({ab}+{bc}+{ac}\right)^{\mathrm{2}} −\mathrm{2}{abc}\left({a}+{b}+{c}\right)= \\ $$$$=\mathrm{2}^{\mathrm{2}} −\mathrm{2}\left(−\mathrm{3}\right)=\mathrm{10} \\ $$$$\Rightarrow\Sigma\left(\frac{\mathrm{1}+\alpha}{\mathrm{1}−\alpha}\right)^{\mathrm{2}} =\mathrm{3}+\mathrm{4}.\mathrm{2}+\mathrm{4}.\mathrm{10}=\mathrm{51} \\ $$$$\Rightarrow\underset{\alpha,\beta,\gamma} {\sum}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)^{\mathrm{2}} =\mathrm{51},\:{x}^{\mathrm{3}} −{x}−\mathrm{1}=\mathrm{0},\:\forall{x}\in\left\{\alpha,\beta,\gamma\right\} \\ $$

Commented by Calculusboy last updated on 25/Dec/23

thanks sir

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com