
Question Number 205682 by naka3546 last updated on 27/Mar/24
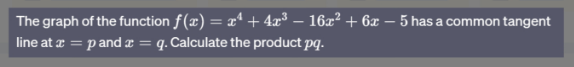
Commented by naka3546 last updated on 28/Mar/24

$$\mathrm{Thank}\:\mathrm{you} \\ $$
Commented by Frix last updated on 28/Mar/24
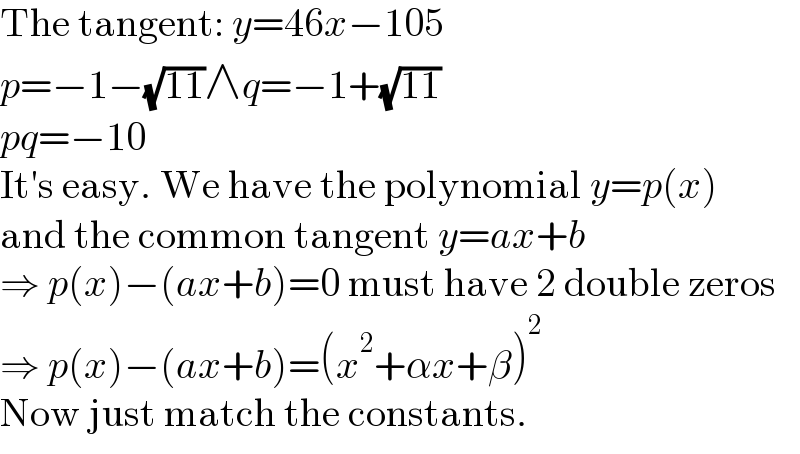
$$\mathrm{The}\:\mathrm{tangent}:\:{y}=\mathrm{46}{x}−\mathrm{105} \\ $$$${p}=−\mathrm{1}−\sqrt{\mathrm{11}}\wedge{q}=−\mathrm{1}+\sqrt{\mathrm{11}} \\ $$$${pq}=−\mathrm{10} \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{easy}.\:\mathrm{We}\:\mathrm{have}\:\mathrm{the}\:\mathrm{polynomial}\:{y}={p}\left({x}\right) \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{common}\:\mathrm{tangent}\:{y}={ax}+{b} \\ $$$$\Rightarrow\:{p}\left({x}\right)−\left({ax}+{b}\right)=\mathrm{0}\:\mathrm{must}\:\mathrm{have}\:\mathrm{2}\:\mathrm{double}\:\mathrm{zeros} \\ $$$$\Rightarrow\:{p}\left({x}\right)−\left({ax}+{b}\right)=\left({x}^{\mathrm{2}} +\alpha{x}+\beta\right)^{\mathrm{2}} \\ $$$$\mathrm{Now}\:\mathrm{just}\:\mathrm{match}\:\mathrm{the}\:\mathrm{constants}. \\ $$
Answered by mr W last updated on 28/Mar/24
![curve: f(x)=x^4 +4x^3 −16x^2 +6x−5 tangent line: h(x)=mx+c difference between them: g(x)=f(x)−h(x) g(x)=x^4 +4x^3 −16x^2 +(6−m)x−(5+c) at x=p, q: g(x)=0 g(x)=(x−p)(x−q)(x^2 +ux+v) g′(x)=(x−p)(x−q)(2x+u)+(2x−p−q)(x^2 +ux+v) at x=p, q: g′(x)=0 g′(p)=(p−q)(p^2 +up+v)=0 g′(q)=(q−p)(q^2 +uq+v)=0 ⇒p^2 +up+v=0, q^2 +qu+v=0 p, q are roots of x^2 +ux+v=0 ⇒x^2 +ux+v=(x−p)(x−q) ⇒g(x)=[(x−p)(x−q)]^2 g′(x)=4(x−p)(x−q)(x−((p+q)/2)) ⇒ p, q and ((p+q)/2) are roots of g′(x)=0 on the other side: g′(x)=4x^3 +12x^2 −32x+(6−m) p+q+((p+q)/2)=−((12)/4)=−3 ⇒p+q=−2 pq+((p+q)/2)×(p+q)=−((32)/4) pq+((−2)/2)×(−2)=−8 ⇒pq=−10 ✓ pq×((p+q)/2)=−((6−m)/4) (−10)×((−2)/2)=−((6−m)/4) ⇒m=46 g(x)=x^4 +4x^3 −16x^2 −40x−(5+c) g(x)=(x^2 +2x−10)^2 ⇒−5−c=(−10)^2 ⇒c=−105 ⇒tangent line: y=46x−105](Q205731.png)
$${curve}:\:{f}\left({x}\right)={x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} −\mathrm{16}{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{5} \\ $$$${tangent}\:{line}:\:{h}\left({x}\right)={mx}+{c} \\ $$$${difference}\:{between}\:{them}: \\ $$$${g}\left({x}\right)={f}\left({x}\right)−{h}\left({x}\right) \\ $$$${g}\left({x}\right)={x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} −\mathrm{16}{x}^{\mathrm{2}} +\left(\mathrm{6}−{m}\right){x}−\left(\mathrm{5}+{c}\right) \\ $$$${at}\:{x}={p},\:{q}:\:{g}\left({x}\right)=\mathrm{0} \\ $$$${g}\left({x}\right)=\left({x}−{p}\right)\left({x}−{q}\right)\left({x}^{\mathrm{2}} +{ux}+{v}\right) \\ $$$${g}'\left({x}\right)=\left({x}−{p}\right)\left({x}−{q}\right)\left(\mathrm{2}{x}+{u}\right)+\left(\mathrm{2}{x}−{p}−{q}\right)\left({x}^{\mathrm{2}} +{ux}+{v}\right) \\ $$$${at}\:{x}={p},\:{q}:\:{g}'\left({x}\right)=\mathrm{0} \\ $$$${g}'\left({p}\right)=\left({p}−{q}\right)\left({p}^{\mathrm{2}} +{up}+{v}\right)=\mathrm{0} \\ $$$${g}'\left({q}\right)=\left({q}−{p}\right)\left({q}^{\mathrm{2}} +{uq}+{v}\right)=\mathrm{0} \\ $$$$\Rightarrow{p}^{\mathrm{2}} +{up}+{v}=\mathrm{0},\:{q}^{\mathrm{2}} +{qu}+{v}=\mathrm{0} \\ $$$${p},\:{q}\:{are}\:{roots}\:{of}\:{x}^{\mathrm{2}} +{ux}+{v}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{ux}+{v}=\left({x}−{p}\right)\left({x}−{q}\right) \\ $$$$\Rightarrow{g}\left({x}\right)=\left[\left({x}−{p}\right)\left({x}−{q}\right)\right]^{\mathrm{2}} \\ $$$${g}'\left({x}\right)=\mathrm{4}\left({x}−{p}\right)\left({x}−{q}\right)\left({x}−\frac{{p}+{q}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:{p},\:{q}\:{and}\:\frac{{p}+{q}}{\mathrm{2}}\:{are}\:{roots}\:{of}\:{g}'\left({x}\right)=\mathrm{0} \\ $$$${on}\:{the}\:{other}\:{side}: \\ $$$${g}'\left({x}\right)=\mathrm{4}{x}^{\mathrm{3}} +\mathrm{12}{x}^{\mathrm{2}} −\mathrm{32}{x}+\left(\mathrm{6}−{m}\right) \\ $$$${p}+{q}+\frac{{p}+{q}}{\mathrm{2}}=−\frac{\mathrm{12}}{\mathrm{4}}=−\mathrm{3} \\ $$$$\Rightarrow{p}+{q}=−\mathrm{2} \\ $$$${pq}+\frac{{p}+{q}}{\mathrm{2}}×\left({p}+{q}\right)=−\frac{\mathrm{32}}{\mathrm{4}} \\ $$$${pq}+\frac{−\mathrm{2}}{\mathrm{2}}×\left(−\mathrm{2}\right)=−\mathrm{8} \\ $$$$\Rightarrow{pq}=−\mathrm{10}\:\checkmark \\ $$$$ \\ $$$${pq}×\frac{{p}+{q}}{\mathrm{2}}=−\frac{\mathrm{6}−{m}}{\mathrm{4}} \\ $$$$\left(−\mathrm{10}\right)×\frac{−\mathrm{2}}{\mathrm{2}}=−\frac{\mathrm{6}−{m}}{\mathrm{4}} \\ $$$$\Rightarrow{m}=\mathrm{46} \\ $$$${g}\left({x}\right)={x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} −\mathrm{16}{x}^{\mathrm{2}} −\mathrm{40}{x}−\left(\mathrm{5}+{c}\right) \\ $$$${g}\left({x}\right)=\left({x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{10}\right)^{\mathrm{2}} \\ $$$$\Rightarrow−\mathrm{5}−{c}=\left(−\mathrm{10}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{c}=−\mathrm{105} \\ $$$$\Rightarrow{tangent}\:{line}:\:{y}=\mathrm{46}{x}−\mathrm{105} \\ $$
Commented by mr W last updated on 28/Mar/24

Commented by mr W last updated on 29/Mar/24
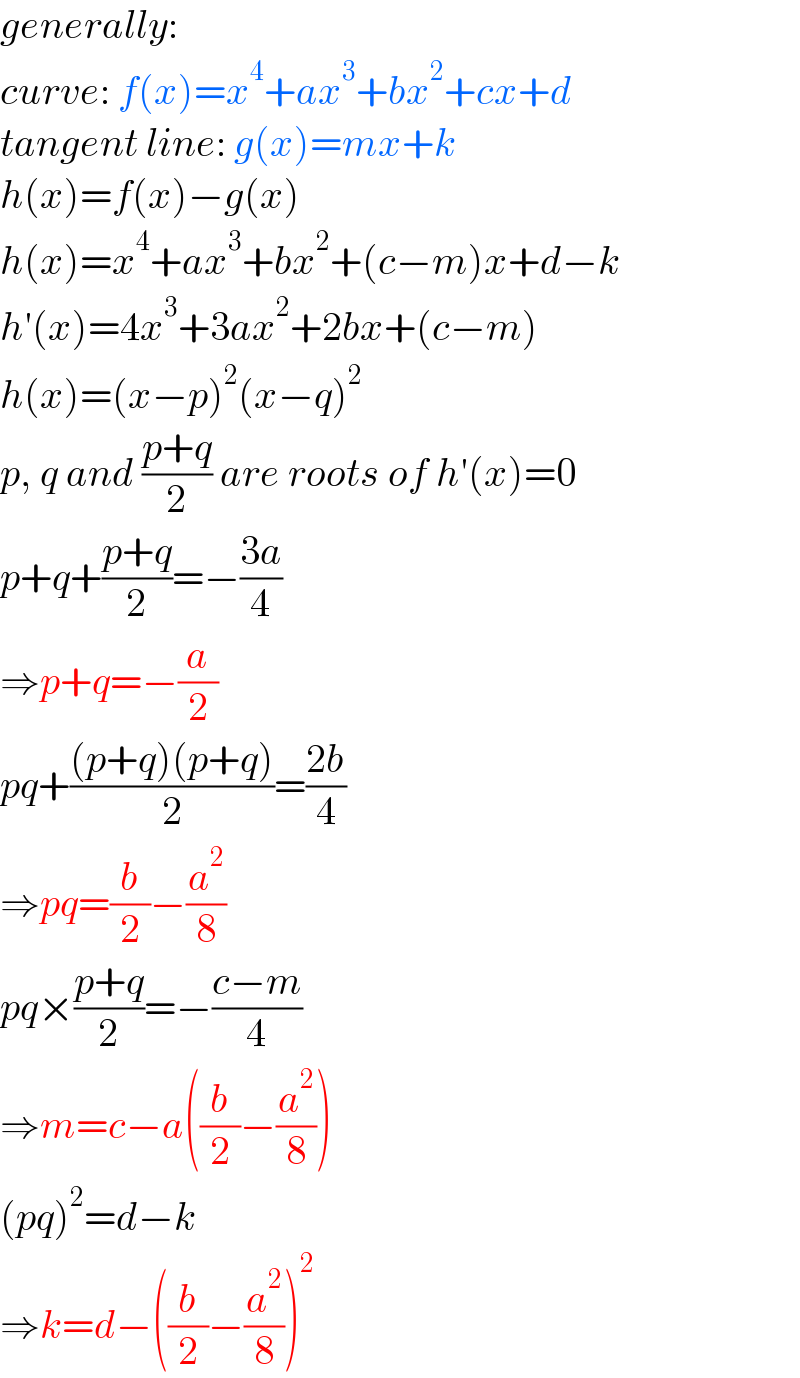
$${generally}: \\ $$$${curve}:\:{f}\left({x}\right)={x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$${tangent}\:{line}:\:{g}\left({x}\right)={mx}+{k} \\ $$$${h}\left({x}\right)={f}\left({x}\right)−{g}\left({x}\right) \\ $$$${h}\left({x}\right)={x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +\left({c}−{m}\right){x}+{d}−{k} \\ $$$${h}'\left({x}\right)=\mathrm{4}{x}^{\mathrm{3}} +\mathrm{3}{ax}^{\mathrm{2}} +\mathrm{2}{bx}+\left({c}−{m}\right) \\ $$$${h}\left({x}\right)=\left({x}−{p}\right)^{\mathrm{2}} \left({x}−{q}\right)^{\mathrm{2}} \\ $$$${p},\:{q}\:{and}\:\frac{{p}+{q}}{\mathrm{2}}\:{are}\:{roots}\:{of}\:{h}'\left({x}\right)=\mathrm{0} \\ $$$${p}+{q}+\frac{{p}+{q}}{\mathrm{2}}=−\frac{\mathrm{3}{a}}{\mathrm{4}} \\ $$$$\Rightarrow{p}+{q}=−\frac{{a}}{\mathrm{2}} \\ $$$${pq}+\frac{\left({p}+{q}\right)\left({p}+{q}\right)}{\mathrm{2}}=\frac{\mathrm{2}{b}}{\mathrm{4}} \\ $$$$\Rightarrow{pq}=\frac{{b}}{\mathrm{2}}−\frac{{a}^{\mathrm{2}} }{\mathrm{8}} \\ $$$${pq}×\frac{{p}+{q}}{\mathrm{2}}=−\frac{{c}−{m}}{\mathrm{4}} \\ $$$$\Rightarrow{m}={c}−{a}\left(\frac{{b}}{\mathrm{2}}−\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\right) \\ $$$$\left({pq}\right)^{\mathrm{2}} ={d}−{k} \\ $$$$\Rightarrow{k}={d}−\left(\frac{{b}}{\mathrm{2}}−\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\right)^{\mathrm{2}} \\ $$
Commented by naka3546 last updated on 30/Mar/24

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
