
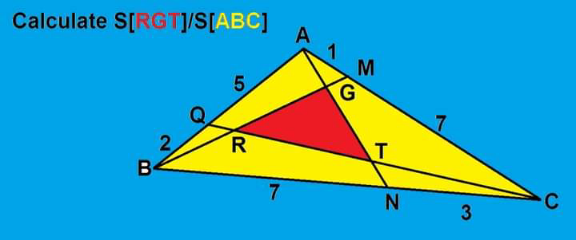
Question Number 206269 by cortano21 last updated on 10/Apr/24
Commented by A5T last updated on 11/Apr/24

Commented by A5T last updated on 11/Apr/24
![General formula. When k_1 k_2 k_3 =1,Ceva′s theorem follows since [P_1 P_2 P_3 ]=0.](Q206290.png)
$${General}\:{formula}.\:{When}\:{k}_{\mathrm{1}} {k}_{\mathrm{2}} {k}_{\mathrm{3}} =\mathrm{1},{Ceva}'{s}\: \\ $$$${theorem}\:{follows}\:{since}\:\left[{P}_{\mathrm{1}} {P}_{\mathrm{2}} {P}_{\mathrm{3}} \right]=\mathrm{0}. \\ $$
Answered by TonyCWX08 last updated on 11/Apr/24

$${Using}\:{Heron}'{s}\:{Formula}: \\ $$$${S}_{{ABC}} =\mathrm{15}\sqrt{\mathrm{510}} \\ $$$${Using}\:{Routh}'{s}\:{Theorem}: \\ $$$${S}_{{RGT}} =\frac{\left(\mathrm{7}×\mathrm{7}×\mathrm{5}\right)^{\mathrm{2}} \left(\mathrm{15}\sqrt{\mathrm{510}}\right)}{\left(\mathrm{7}\left(\mathrm{7}\right)+\mathrm{7}+\mathrm{1}\right)\left(\mathrm{7}\left(\mathrm{5}\right)+\mathrm{5}+\mathrm{1}\right)\left(\mathrm{5}\left(\mathrm{7}\right)+\mathrm{7}+\mathrm{1}\right)} \\ $$$${S}_{{RGT}} =\frac{\mathrm{60025}\left(\mathrm{15}\sqrt{\mathrm{510}}\right)}{\left(\mathrm{57}\right)\left(\mathrm{41}\right)\left(\mathrm{43}\right)} \\ $$$${S}_{{RGT}} =\frac{\mathrm{60025}\left(\mathrm{15}\sqrt{\mathrm{510}}\right)}{\mathrm{100491}} \\ $$$${S}_{{RGT}} =\frac{\mathrm{60025}\left(\mathrm{15}\sqrt{\mathrm{510}}\right)}{\mathrm{100491}} \\ $$$${S}_{{RGT}} =\frac{\mathrm{300125}\sqrt{\mathrm{510}}}{\mathrm{33497}} \\ $$$${Finally}: \\ $$$$\frac{{S}_{{RGT}} }{{S}_{{ABC}} }=\frac{\mathrm{300125}\sqrt{\mathrm{510}}}{\mathrm{33497}}×\frac{\mathrm{1}}{\mathrm{15}\sqrt{\mathrm{510}}}=\frac{\mathrm{60025}}{\mathrm{100491}}\approx\mathrm{0}.\mathrm{6} \\ $$
Commented by TonyCWX08 last updated on 11/Apr/24

$${Please}\:{Check}. \\ $$$${I}'{m}\:{a}\:{bit}\:{unsure}. \\ $$
Commented by A5T last updated on 11/Apr/24

$${I}\:{guess}\:{the}\:{formula}\:{above}\:{could}\:{be}\:{the}\:{correct} \\ $$$${application}\:{of}\:{Routh}'{s}\:{theorem}. \\ $$
Answered by mr W last updated on 11/Apr/24
![((MG)/(GB))×(7/3)×(8/1)=1 ⇒((MG)/(GB))=(3/(56)) ⇒[AMG]=(3/(59))[AMB]=(3/(59))×(1/8)[ABC] ((QR)/(RC))×(7/1)×(7/2)=1 ⇒((QR)/(RC))=(2/(49)) ⇒[BQR]=(2/(51))[BQC]=(2/(51))×(2/7)[ABC] ((NT)/(TA))×(5/2)×((10)/3)=1 ⇒((NT)/(TA))=(3/(25)) ⇒[CNT]=(3/(28))[CNA]=(3/(28))×(3/(10))[ABC] [RGT]=[ABC]−[AMB]−[BQC]−[CNA]+[AMG]+[BQR]+[CNT] [RGT]=[ABC]−(1/8)[ABC]−(2/7)[ABC]−(3/(10))[ABC]+(3/(59))×(1/8)[ABC]+(2/(51))×(2/7)[ABC]+(3/(28))×(3/(10))[ABC] (([RGT])/([ABC]))=1−(1/8)−(2/7)−(3/(10))+(3/(59))×(1/8)+(2/(51))×(2/7)+(3/(28))×(3/(10)) =((57121)/(168504))≈0.339](Q206283.png)
$$\frac{{MG}}{{GB}}×\frac{\mathrm{7}}{\mathrm{3}}×\frac{\mathrm{8}}{\mathrm{1}}=\mathrm{1}\:\Rightarrow\frac{{MG}}{{GB}}=\frac{\mathrm{3}}{\mathrm{56}}\: \\ $$$$\Rightarrow\left[{AMG}\right]=\frac{\mathrm{3}}{\mathrm{59}}\left[{AMB}\right]=\frac{\mathrm{3}}{\mathrm{59}}×\frac{\mathrm{1}}{\mathrm{8}}\left[{ABC}\right] \\ $$$$\frac{{QR}}{{RC}}×\frac{\mathrm{7}}{\mathrm{1}}×\frac{\mathrm{7}}{\mathrm{2}}=\mathrm{1}\:\Rightarrow\frac{{QR}}{{RC}}=\frac{\mathrm{2}}{\mathrm{49}} \\ $$$$\Rightarrow\left[{BQR}\right]=\frac{\mathrm{2}}{\mathrm{51}}\left[{BQC}\right]=\frac{\mathrm{2}}{\mathrm{51}}×\frac{\mathrm{2}}{\mathrm{7}}\left[{ABC}\right] \\ $$$$\frac{{NT}}{{TA}}×\frac{\mathrm{5}}{\mathrm{2}}×\frac{\mathrm{10}}{\mathrm{3}}=\mathrm{1}\:\Rightarrow\frac{{NT}}{{TA}}=\frac{\mathrm{3}}{\mathrm{25}} \\ $$$$\Rightarrow\left[{CNT}\right]=\frac{\mathrm{3}}{\mathrm{28}}\left[{CNA}\right]=\frac{\mathrm{3}}{\mathrm{28}}×\frac{\mathrm{3}}{\mathrm{10}}\left[{ABC}\right] \\ $$$$ \\ $$$$\left[{RGT}\right]=\left[{ABC}\right]−\left[{AMB}\right]−\left[{BQC}\right]−\left[{CNA}\right]+\left[{AMG}\right]+\left[{BQR}\right]+\left[{CNT}\right] \\ $$$$\left[{RGT}\right]=\left[{ABC}\right]−\frac{\mathrm{1}}{\mathrm{8}}\left[{ABC}\right]−\frac{\mathrm{2}}{\mathrm{7}}\left[{ABC}\right]−\frac{\mathrm{3}}{\mathrm{10}}\left[{ABC}\right]+\frac{\mathrm{3}}{\mathrm{59}}×\frac{\mathrm{1}}{\mathrm{8}}\left[{ABC}\right]+\frac{\mathrm{2}}{\mathrm{51}}×\frac{\mathrm{2}}{\mathrm{7}}\left[{ABC}\right]+\frac{\mathrm{3}}{\mathrm{28}}×\frac{\mathrm{3}}{\mathrm{10}}\left[{ABC}\right] \\ $$$$\frac{\left[{RGT}\right]}{\left[{ABC}\right]}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{2}}{\mathrm{7}}−\frac{\mathrm{3}}{\mathrm{10}}+\frac{\mathrm{3}}{\mathrm{59}}×\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{2}}{\mathrm{51}}×\frac{\mathrm{2}}{\mathrm{7}}+\frac{\mathrm{3}}{\mathrm{28}}×\frac{\mathrm{3}}{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{57121}}{\mathrm{168504}}\approx\mathrm{0}.\mathrm{339} \\ $$
Commented by TonyCWX08 last updated on 11/Apr/24

$${Why}\:{equal}\:{to}\:\mathrm{1}? \\ $$
Commented by cortano21 last updated on 11/Apr/24

$${Menelous}\:{theorem} \\ $$
Commented by mr W last updated on 11/Apr/24

Answered by A5T last updated on 11/Apr/24
![[BQC]=(2/7)[ABC]=[BQR]+[BRTN]+[TNC] [BAM]=(1/8)[ABC]=[BQR]+[QRGA]+[AGM] [ANC]=(3/(10))[ABC]=[AGM]+[MGTC]+[TNC] ⇒[ABC]((2/7)+(1/8)+(3/(10)))=[ABC]−[GRT]+[BQR] +[TNC]+[AGM]...(i) ((QR)/(RC))×(7/1)×(7/2)=1⇒((QR)/(RC))=(2/(49))⇒[BQR]=((4[ABC])/(51×7)) (7/3)×(8/1)×((MG)/(GB))=1⇒((MG)/(GB))=(3/(56))⇒[AMG]=((3[ABC])/(472)) (5/2)×((10)/3)×((NT)/(TA))=1⇒((NT)/(TA))=(3/(25))⇒[CNT]=(9/(280))[ABC] (i)⇒(([GRT])/([ABC]))=1−(2/7)−(1/8)−(3/(10))+(4/(357))+(3/(472))+(9/(280)) =((57121)/(168504))≈0.339](Q206288.png)
$$\left[{BQC}\right]=\frac{\mathrm{2}}{\mathrm{7}}\left[{ABC}\right]=\left[{BQR}\right]+\left[{BRTN}\right]+\left[{TNC}\right] \\ $$$$\left[{BAM}\right]=\frac{\mathrm{1}}{\mathrm{8}}\left[{ABC}\right]=\left[{BQR}\right]+\left[{QRGA}\right]+\left[{AGM}\right] \\ $$$$\left[{ANC}\right]=\frac{\mathrm{3}}{\mathrm{10}}\left[{ABC}\right]=\left[{AGM}\right]+\left[{MGTC}\right]+\left[{TNC}\right] \\ $$$$\Rightarrow\left[{ABC}\right]\left(\frac{\mathrm{2}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{3}}{\mathrm{10}}\right)=\left[{ABC}\right]−\left[{GRT}\right]+\left[{BQR}\right] \\ $$$$+\left[{TNC}\right]+\left[{AGM}\right]...\left({i}\right) \\ $$$$\frac{{QR}}{{RC}}×\frac{\mathrm{7}}{\mathrm{1}}×\frac{\mathrm{7}}{\mathrm{2}}=\mathrm{1}\Rightarrow\frac{{QR}}{{RC}}=\frac{\mathrm{2}}{\mathrm{49}}\Rightarrow\left[{BQR}\right]=\frac{\mathrm{4}\left[{ABC}\right]}{\mathrm{51}×\mathrm{7}} \\ $$$$\frac{\mathrm{7}}{\mathrm{3}}×\frac{\mathrm{8}}{\mathrm{1}}×\frac{{MG}}{{GB}}=\mathrm{1}\Rightarrow\frac{{MG}}{{GB}}=\frac{\mathrm{3}}{\mathrm{56}}\Rightarrow\left[{AMG}\right]=\frac{\mathrm{3}\left[{ABC}\right]}{\mathrm{472}} \\ $$$$\frac{\mathrm{5}}{\mathrm{2}}×\frac{\mathrm{10}}{\mathrm{3}}×\frac{{NT}}{{TA}}=\mathrm{1}\Rightarrow\frac{{NT}}{{TA}}=\frac{\mathrm{3}}{\mathrm{25}}\Rightarrow\left[{CNT}\right]=\frac{\mathrm{9}}{\mathrm{280}}\left[{ABC}\right] \\ $$$$\left({i}\right)\Rightarrow\frac{\left[{GRT}\right]}{\left[{ABC}\right]}=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{3}}{\mathrm{10}}+\frac{\mathrm{4}}{\mathrm{357}}+\frac{\mathrm{3}}{\mathrm{472}}+\frac{\mathrm{9}}{\mathrm{280}} \\ $$$$=\frac{\mathrm{57121}}{\mathrm{168504}}\approx\mathrm{0}.\mathrm{339} \\ $$
