Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 195790 by justenspi last updated on 10/Aug/23

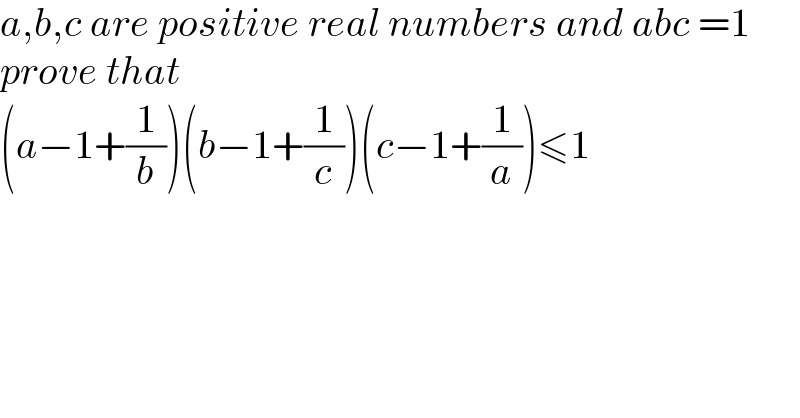
a,b,c are positive real numbers and abc =1 prove that (a−1+(1/b))(b−1+(1/c))(c−1+(1/a))≤1

$${a},{b},{c}\:{are}\:{positive}\:{real}\:{numbers}\:{and}\:{abc}\:=\mathrm{1} \\ $$$${prove}\:{that} \\ $$$$\left({a}−\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left({b}−\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\left({c}−\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)\leqslant\mathrm{1} \\ $$

Commented by justenspi last updated on 10/Aug/23

Case(I)(a−1+(1/b)),(b−1+(1/c)),(c−1+(1/a))>0 ⇒(((a−1+(1/b))(b−1+(1/c))(c−1+(1/a))))^(1/3) ≤((a+b+c+ab+bc+ac−3)/3)......(i) ⇒(((a−1+(1/b))(b−1+(1/c))(c−1+(1/a))))^(1/3) ≤((ab+bc+ac−a−b−c+3)/3)......(ii) ⇒2(((a−1+(1/b))(b−1+(1/c))(c−1+(1/a))))^(1/3) ≤((2(ab+bc+ac))/3) ⇒(((a−1+(1/b))(b−1+(1/c))(c−1+(1/a))))^(1/3) ≤((ab+bc+ac)/3) the equality holds when a+b+c=ab+bc+ac∧abc=1∧a,b,c>0 ⇒a+b+c=(1/a)+(1/b)+(1/c)⇒a=1,b=1,c=1 hence the maximum value of (((a−1+(1/b))(b−1+(1/c))(c−1+(1/a))))^(1/3) →((1+1+1)/3)=1 ⇒(a−1+(1/b))(b−1+(1/c))(c−1+(1/a)) max =1 Case(II) At most one the factors is negative hence we are done

$${Case}\left({I}\right)\left({a}−\mathrm{1}+\frac{\mathrm{1}}{{b}}\right),\left({b}−\mathrm{1}+\frac{\mathrm{1}}{{c}}\right),\left({c}−\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)>\mathrm{0} \\ $$$$\Rightarrow\sqrt[{\mathrm{3}}]{\left({a}−\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left({b}−\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\left({c}−\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)}\leqslant\frac{{a}+{b}+{c}+{ab}+{bc}+{ac}−\mathrm{3}}{\mathrm{3}}......\left({i}\right) \\ $$$$\Rightarrow\sqrt[{\mathrm{3}}]{\left({a}−\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left({b}−\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\left({c}−\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)}\leqslant\frac{{ab}+{bc}+{ac}−{a}−{b}−{c}+\mathrm{3}}{\mathrm{3}}......\left({ii}\right) \\ $$$$\Rightarrow\mathrm{2}\sqrt[{\mathrm{3}}]{\left({a}−\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left({b}−\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\left({c}−\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)}\leqslant\frac{\mathrm{2}\left({ab}+{bc}+{ac}\right)}{\mathrm{3}} \\ $$$$\Rightarrow\sqrt[{\mathrm{3}}]{\left({a}−\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left({b}−\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\left({c}−\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)}\leqslant\frac{{ab}+{bc}+{ac}}{\mathrm{3}} \\ $$$${the}\:{equality}\:{holds}\:{when} \\ $$$${a}+{b}+{c}={ab}+{bc}+{ac}\wedge{abc}=\mathrm{1}\wedge{a},{b},{c}>\mathrm{0} \\ $$$$\Rightarrow{a}+{b}+{c}=\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\Rightarrow{a}=\mathrm{1},{b}=\mathrm{1},{c}=\mathrm{1} \\ $$$${hence}\:{the}\:{maximum}\:{value}\:{of} \\ $$$$\sqrt[{\mathrm{3}}]{\left({a}−\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left({b}−\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\left({c}−\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)}\rightarrow\frac{\mathrm{1}+\mathrm{1}+\mathrm{1}}{\mathrm{3}}=\mathrm{1} \\ $$$$\Rightarrow\left({a}−\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left({b}−\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\left({c}−\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)\:{max}\:=\mathrm{1} \\ $$$${Case}\left({II}\right)\:{At}\:{most}\:{one}\:{the}\:{factors}\:{is}\:{negative} \\ $$$${hence}\:{we}\:{are}\:{done} \\ $$

Commented by justenspi last updated on 10/Aug/23

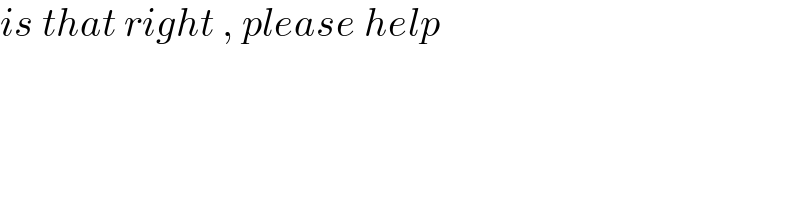
is that right , please help

$${is}\:{that}\:{right}\:,\:{please}\:{help}\: \\ $$

Answered by York12 last updated on 10/Aug/23

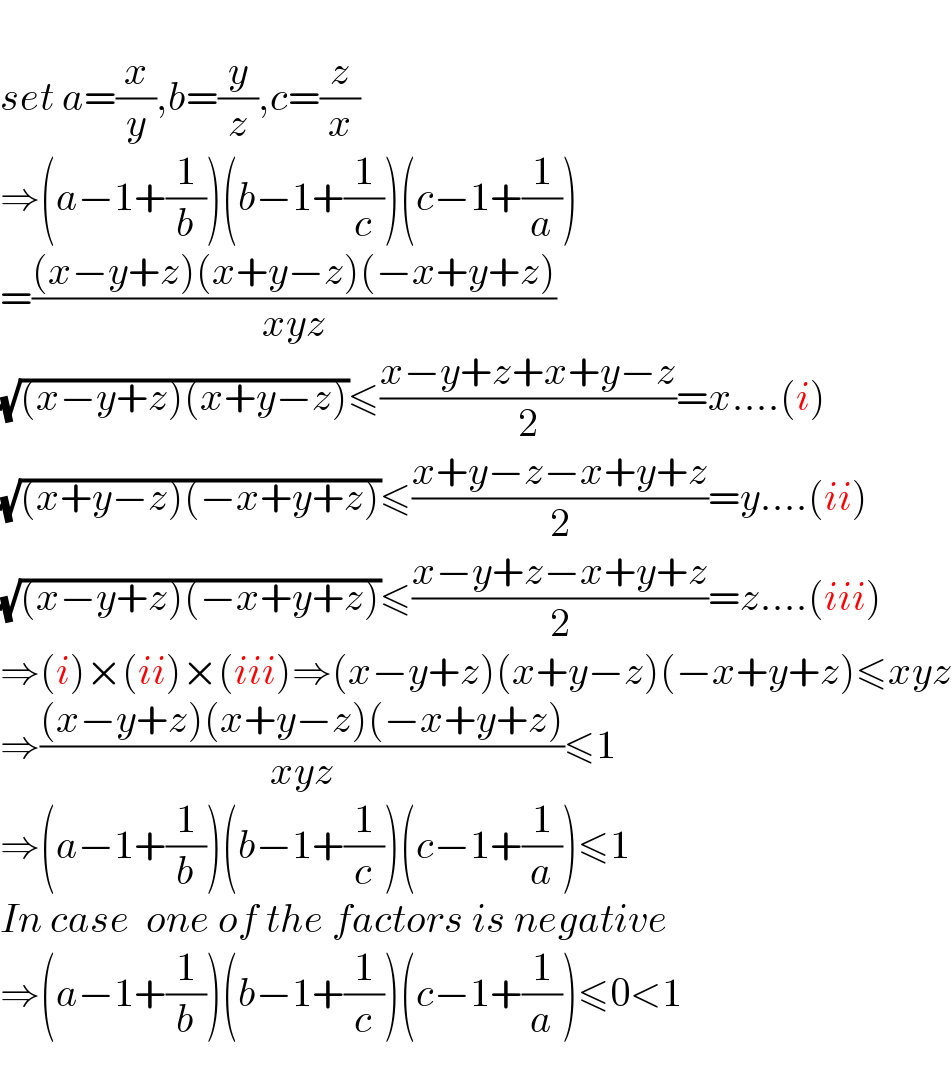
set a=(x/y),b=(y/z),c=(z/x) ⇒(a−1+(1/b))(b−1+(1/c))(c−1+(1/a)) =(((x−y+z)(x+y−z)(−x+y+z))/(xyz)) (√((x−y+z)(x+y−z)))≤((x−y+z+x+y−z)/2)=x....(i) (√((x+y−z)(−x+y+z)))≤((x+y−z−x+y+z)/2)=y....(ii) (√((x−y+z)(−x+y+z)))≤((x−y+z−x+y+z)/2)=z....(iii) ⇒(i)×(ii)×(iii)⇒(x−y+z)(x+y−z)(−x+y+z)≤xyz ⇒(((x−y+z)(x+y−z)(−x+y+z))/(xyz))≤1 ⇒(a−1+(1/b))(b−1+(1/c))(c−1+(1/a))≤1 In case one of the factors is negative ⇒(a−1+(1/b))(b−1+(1/c))(c−1+(1/a))≤0<1

$$ \\ $$$${set}\:{a}=\frac{{x}}{{y}},{b}=\frac{{y}}{{z}},{c}=\frac{{z}}{{x}} \\ $$$$\Rightarrow\left({a}−\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left({b}−\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\left({c}−\mathrm{1}+\frac{\mathrm{1}}{{a}}\right) \\ $$$$=\frac{\left({x}−{y}+{z}\right)\left({x}+{y}−{z}\right)\left(−{x}+{y}+{z}\right)}{{xyz}} \\ $$$$\sqrt{\left({x}−{y}+{z}\right)\left({x}+{y}−{z}\right)}\leqslant\frac{{x}−{y}+{z}+{x}+{y}−{z}}{\mathrm{2}}={x}....\left({i}\right) \\ $$$$\sqrt{\left({x}+{y}−{z}\right)\left(−{x}+{y}+{z}\right)}\leqslant\frac{{x}+{y}−{z}−{x}+{y}+{z}}{\mathrm{2}}={y}....\left({ii}\right) \\ $$$$\sqrt{\left({x}−{y}+{z}\right)\left(−{x}+{y}+{z}\right)}\leqslant\frac{{x}−{y}+{z}−{x}+{y}+{z}}{\mathrm{2}}={z}....\left({iii}\right) \\ $$$$\Rightarrow\left({i}\right)×\left({ii}\right)×\left({iii}\right)\Rightarrow\left({x}−{y}+{z}\right)\left({x}+{y}−{z}\right)\left(−{x}+{y}+{z}\right)\leqslant{xyz} \\ $$$$\Rightarrow\frac{\left({x}−{y}+{z}\right)\left({x}+{y}−{z}\right)\left(−{x}+{y}+{z}\right)}{{xyz}}\leqslant\mathrm{1} \\ $$$$\Rightarrow\left({a}−\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left({b}−\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\left({c}−\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)\leqslant\mathrm{1} \\ $$$${In}\:{case}\:\:{one}\:{of}\:{the}\:{factors}\:{is}\:{negative} \\ $$$$\Rightarrow\left({a}−\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left({b}−\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\left({c}−\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)\leqslant\mathrm{0}<\mathrm{1}\: \\ $$

Commented by justenspi last updated on 10/Aug/23

thanks but is my solution right

$${thanks}\:{but}\:{is}\:{my}\:{solution}\:{right} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com