Question Number 10876 by Saham last updated on 28/Feb/17
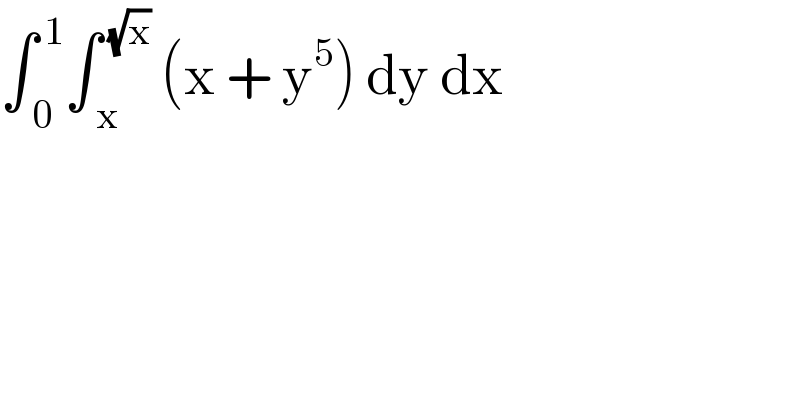
$$\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \int_{\:\mathrm{x}} ^{\:\sqrt{\mathrm{x}}} \:\left(\mathrm{x}\:+\:\mathrm{y}^{\mathrm{5}} \right)\:\mathrm{dy}\:\mathrm{dx} \\ $$
Answered by fariraihmudzengerere75@gmail.c last updated on 28/Feb/17
![Answer . ∫_0 ^1 ∫_x ^(√x) (x+y^5 )dydx =∫_0 ^1 [ xy +(y^6 /6)+c ]_x ^(√x) dx =∫_0 ^1 [x×(√(x )) +((((√(x)^6 )))/6)−x^(2 ) −(x^6 /6) +c−c]dx =∫_0 ^1 [x^(3/2) + (x^3 /6) −x^2 −(x^6 /6)]dx =[(x^(5/2) /(5/2))+(x^4 /(24)) −(x^3 /3) −(x^7 /(42)) +c−c]_0 ^1 =(2/5)+(1/(24))−(1/3)−(1/(42)) =0 .084 523 809](https://www.tinkutara.com/question/Q10879.png)
$${Answer}\:.\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\int_{{x}} ^{\sqrt{{x}}} \:\:\left({x}+{y}^{\mathrm{5}} \right){dydx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left[\:\:{xy}\:+\frac{{y}^{\mathrm{6}} }{\mathrm{6}}+{c}\:\right]_{{x}} ^{\sqrt{{x}}} {dx}\: \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left[{x}×\sqrt{{x}\:}\:\:+\frac{\left(\sqrt{\left.{x}\right)^{\mathrm{6}} \:\:\:\:}\right.}{\mathrm{6}}−{x}^{\mathrm{2}\:\:} −\frac{{x}^{\mathrm{6}} }{\mathrm{6}}\:\:\:+{c}−{c}\right]{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left[{x}^{\mathrm{3}/\mathrm{2}} +\:\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\:−{x}^{\mathrm{2}} −\frac{{x}^{\mathrm{6}} }{\mathrm{6}}\right]{dx} \\ $$$$=\left[\frac{{x}^{\mathrm{5}/\mathrm{2}} }{\mathrm{5}/\mathrm{2}}+\frac{{x}^{\mathrm{4}} }{\mathrm{24}}\:−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:−\frac{{x}^{\mathrm{7}} }{\mathrm{42}}\:\:+{c}−{c}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{24}}−\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{42}} \\ $$$$=\mathrm{0}\:.\mathrm{084}\:\:\mathrm{523}\:\:\mathrm{809} \\ $$
Commented by Saham last updated on 28/Feb/17
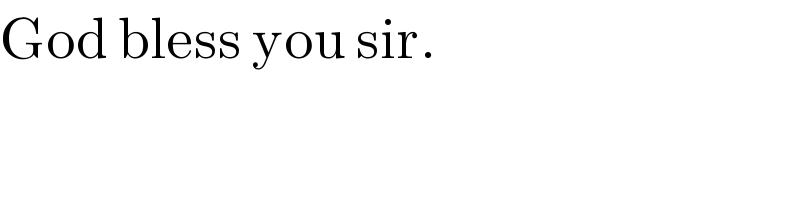
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
