Question Number 137345 by liberty last updated on 01/Apr/21
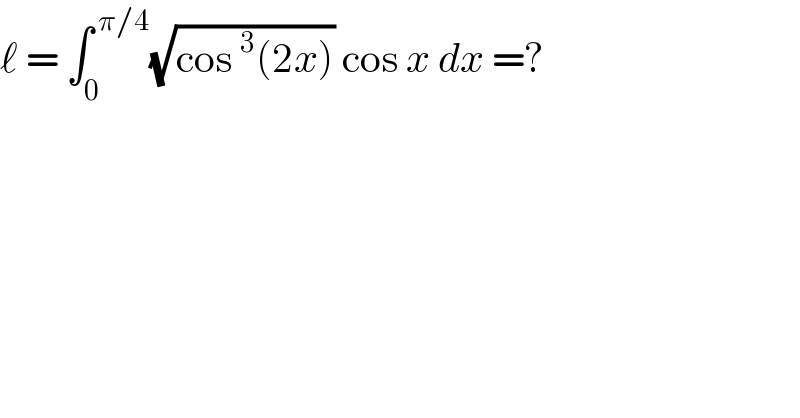
$$\ell\:=\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \sqrt{\mathrm{cos}\:^{\mathrm{3}} \left(\mathrm{2}{x}\right)}\:\mathrm{cos}\:{x}\:{dx}\:=?\: \\ $$
Answered by MJS_new last updated on 01/Apr/21
![∫cos^(3/2) 2x cos x dx= [t=(((√2)sin x)/(cos^(1/2) 2x)) → dx=((cos^(3/2) 2x)/( (√2)cos x))] =(1/( (√2)))∫(dt/((t^2 +1)^3 ))= [Ostrogradski] =(((√2)(3t^2 +5)t)/(16(t^2 +1)))+((3(√2))/(16))∫(dt/(t^2 +1))= =(((√2)(3t^2 +5)t)/(16(t^2 +1)))+((3(√2))/(16))arctan t = =((sin x (3+cos 2x)cos^(1/2) 2x)/8)+((3(√2)arcsin ((√2)sin x))/(16))+C ⇒ answer is ((3(√2)π)/(32))](https://www.tinkutara.com/question/Q137358.png)
$$\int\mathrm{cos}^{\mathrm{3}/\mathrm{2}} \:\mathrm{2}{x}\:\mathrm{cos}\:{x}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{2}}\mathrm{sin}\:{x}}{\mathrm{cos}^{\mathrm{1}/\mathrm{2}} \:\mathrm{2}{x}}\:\rightarrow\:{dx}=\frac{\mathrm{cos}^{\mathrm{3}/\mathrm{2}} \:\mathrm{2}{x}}{\:\sqrt{\mathrm{2}}\mathrm{cos}\:{x}}\right] \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{5}\right){t}}{\mathrm{16}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{16}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=\frac{\sqrt{\mathrm{2}}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{5}\right){t}}{\mathrm{16}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{16}}\mathrm{arctan}\:{t}\:= \\ $$$$=\frac{\mathrm{sin}\:{x}\:\left(\mathrm{3}+\mathrm{cos}\:\mathrm{2}{x}\right)\mathrm{cos}^{\mathrm{1}/\mathrm{2}} \:\mathrm{2}{x}}{\mathrm{8}}+\frac{\mathrm{3}\sqrt{\mathrm{2}}\mathrm{arcsin}\:\left(\sqrt{\mathrm{2}}\mathrm{sin}\:{x}\right)}{\mathrm{16}}+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{3}\sqrt{\mathrm{2}}\pi}{\mathrm{32}} \\ $$
