Question Number 6979 by Fitrah A last updated on 04/Aug/16
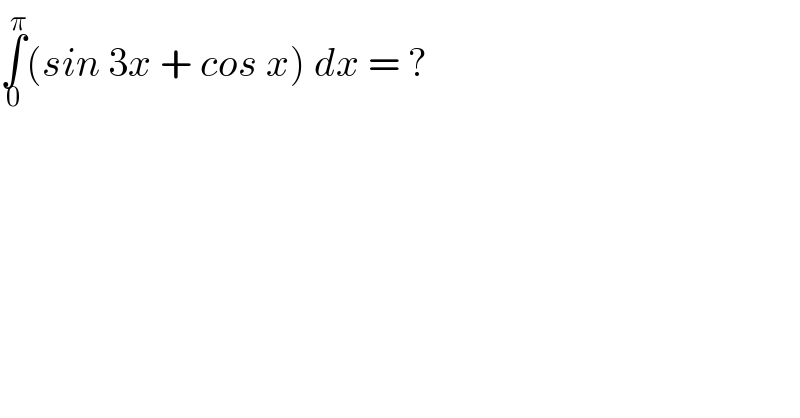
$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\left({sin}\:\mathrm{3}{x}\:+\:{cos}\:{x}\right)\:{dx}\:=\:? \\ $$
Answered by sandy_suhendra last updated on 04/Aug/16
![=[−(1/3)cos 3x + sin x]_0 ^π =(−(1/3) cos 3π + sin π)−(−(1/3) cos 0 + sin 0) =((1/3) + 0)−(−(1/3)+0) =(2/3)](https://www.tinkutara.com/question/Q6980.png)
$$=\left[−\frac{\mathrm{1}}{\mathrm{3}}{cos}\:\mathrm{3}{x}\:+\:{sin}\:{x}\right]_{\mathrm{0}} ^{\pi} \\ $$$$=\left(−\frac{\mathrm{1}}{\mathrm{3}}\:{cos}\:\mathrm{3}\pi\:+\:{sin}\:\pi\right)−\left(−\frac{\mathrm{1}}{\mathrm{3}}\:{cos}\:\mathrm{0}\:+\:{sin}\:\mathrm{0}\right) \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{3}}\:+\:\mathrm{0}\right)−\left(−\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{0}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
