Question Number 139978 by mathdanisur last updated on 02/May/21
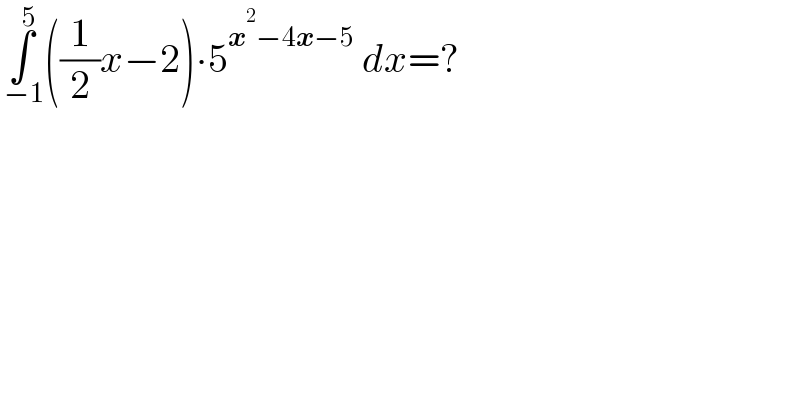
$$\underset{\:−\mathrm{1}} {\overset{\:\mathrm{5}} {\int}}\left(\frac{\mathrm{1}}{\mathrm{2}}{x}−\mathrm{2}\right)\centerdot\mathrm{5}^{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{{x}}−\mathrm{5}} \:{dx}=? \\ $$
Answered by MJS_new last updated on 03/May/21
![∫((1/2)x−2)5^(x^2 −4x−5) dx= [t=x−2 → dx=dt] =(1/2)∫(t−2)5^(t^2 −9) dt=(1/(2×5^9 ))∫(t−2)5^t^2 dt= =(1/(3906250))∫(t×5^t^2 −2×5^t^2 )dt= =(1/(7812500))∫2t×5^t^2 dt−(1/(1953125))∫5^t^2 dt= ∫2t×5^t^2 dt=(5^t^2 /(ln 5))=(5^((x−2)^2 ) /(ln 5))=((1953125×5^(x^2 −4x−5) )/(ln 5)) ∫5^t^2 dt= [u=(√(ln 5))t → dt=(du/( (√(ln 5))))] =(1/( (√(ln 5))))∫e^u^2 du=((√π)/(2(√(ln 5))))∫(2/( (√π)))e^u^2 du=((√π)/(2(√(ln 5))))erfi u = =((√π)/(2(√(ln 5))))erfi ((√(ln 5))t) =((√π)/(2(√(ln 5))))erfi ((√(ln 5))(x−2)) =(5^(x^2 −4x−5) /(4ln 5))−(((√π)erfi ((√(ln 5))(x−2)))/(3906250(√(ln 5))))+C now insert borders](https://www.tinkutara.com/question/Q139997.png)
$$\int\left(\frac{\mathrm{1}}{\mathrm{2}}{x}−\mathrm{2}\right)\mathrm{5}^{{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{5}} {dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}−\mathrm{2}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left({t}−\mathrm{2}\right)\mathrm{5}^{{t}^{\mathrm{2}} −\mathrm{9}} {dt}=\frac{\mathrm{1}}{\mathrm{2}×\mathrm{5}^{\mathrm{9}} }\int\left({t}−\mathrm{2}\right)\mathrm{5}^{{t}^{\mathrm{2}} } {dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3906250}}\int\left({t}×\mathrm{5}^{{t}^{\mathrm{2}} } −\mathrm{2}×\mathrm{5}^{{t}^{\mathrm{2}} } \right){dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{7812500}}\int\mathrm{2}{t}×\mathrm{5}^{{t}^{\mathrm{2}} } {dt}−\frac{\mathrm{1}}{\mathrm{1953125}}\int\mathrm{5}^{{t}^{\mathrm{2}} } {dt}= \\ $$$$ \\ $$$$\int\mathrm{2}{t}×\mathrm{5}^{{t}^{\mathrm{2}} } {dt}=\frac{\mathrm{5}^{{t}^{\mathrm{2}} } }{\mathrm{ln}\:\mathrm{5}}=\frac{\mathrm{5}^{\left({x}−\mathrm{2}\right)^{\mathrm{2}} } }{\mathrm{ln}\:\mathrm{5}}=\frac{\mathrm{1953125}×\mathrm{5}^{{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{5}} }{\mathrm{ln}\:\mathrm{5}} \\ $$$$\int\mathrm{5}^{{t}^{\mathrm{2}} } {dt}= \\ $$$$\:\:\:\:\:\left[{u}=\sqrt{\mathrm{ln}\:\mathrm{5}}{t}\:\rightarrow\:{dt}=\frac{{du}}{\:\sqrt{\mathrm{ln}\:\mathrm{5}}}\right] \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{ln}\:\mathrm{5}}}\int\mathrm{e}^{{u}^{\mathrm{2}} } {du}=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{ln}\:\mathrm{5}}}\int\frac{\mathrm{2}}{\:\sqrt{\pi}}\mathrm{e}^{{u}^{\mathrm{2}} } {du}=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{ln}\:\mathrm{5}}}\mathrm{erfi}\:{u}\:= \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{ln}\:\mathrm{5}}}\mathrm{erfi}\:\left(\sqrt{\mathrm{ln}\:\mathrm{5}}{t}\right)\:=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{ln}\:\mathrm{5}}}\mathrm{erfi}\:\left(\sqrt{\mathrm{ln}\:\mathrm{5}}\left({x}−\mathrm{2}\right)\right) \\ $$$$ \\ $$$$=\frac{\mathrm{5}^{{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{5}} }{\mathrm{4ln}\:\mathrm{5}}−\frac{\sqrt{\pi}\mathrm{erfi}\:\left(\sqrt{\mathrm{ln}\:\mathrm{5}}\left({x}−\mathrm{2}\right)\right)}{\mathrm{3906250}\sqrt{\mathrm{ln}\:\mathrm{5}}}+{C} \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{insert}\:\mathrm{borders} \\ $$
Commented by mathdanisur last updated on 03/May/21
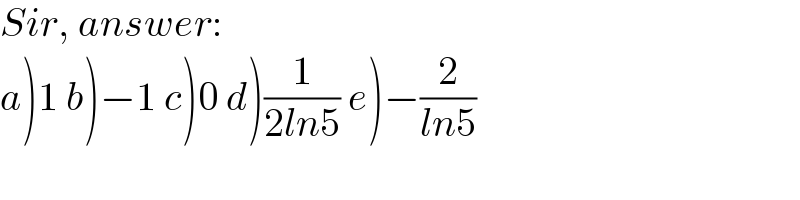
$${Sir},\:{answer}: \\ $$$$\left.{a}\left.\right)\left.\mathrm{1}\left.\:\left.{b}\right)−\mathrm{1}\:{c}\right)\mathrm{0}\:{d}\right)\frac{\mathrm{1}}{\mathrm{2}{ln}\mathrm{5}}\:{e}\right)−\frac{\mathrm{2}}{{ln}\mathrm{5}} \\ $$
Commented by MJS_new last updated on 03/May/21
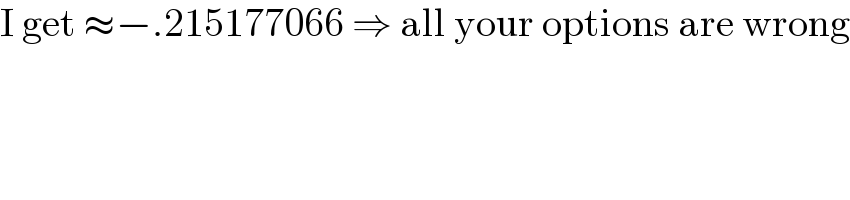
$$\mathrm{I}\:\mathrm{get}\:\approx−.\mathrm{215177066}\:\Rightarrow\:\mathrm{all}\:\mathrm{your}\:\mathrm{options}\:\mathrm{are}\:\mathrm{wrong} \\ $$
Commented by mathdanisur last updated on 03/May/21

$${thankyou}\:{Sir} \\ $$
