Question Number 7713 by Tawakalitu. last updated on 11/Sep/16
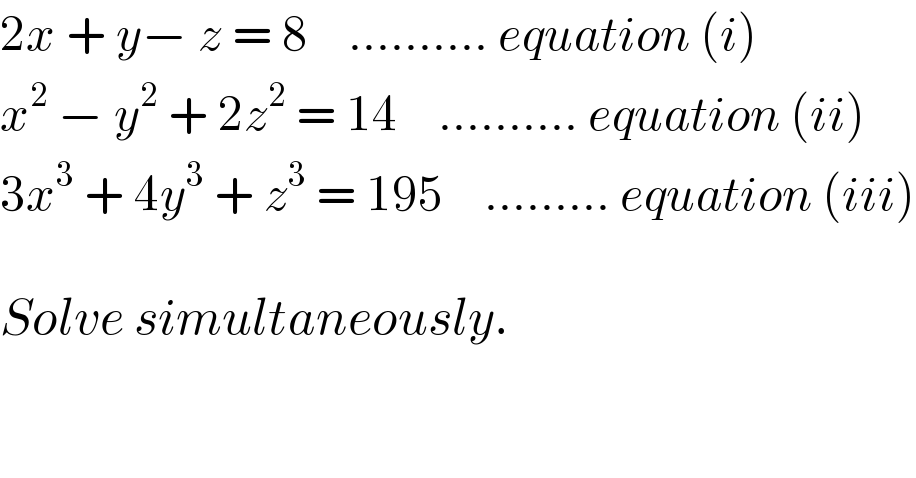
$$\mathrm{2}{x}\:+\:{y}−\:{z}\:=\:\mathrm{8}\:\:\:\:……….\:{equation}\:\left({i}\right) \\ $$$${x}^{\mathrm{2}} \:−\:{y}^{\mathrm{2}} \:+\:\mathrm{2}{z}^{\mathrm{2}} \:=\:\mathrm{14}\:\:\:\:……….\:{equation}\:\left({ii}\right) \\ $$$$\mathrm{3}{x}^{\mathrm{3}} \:+\:\mathrm{4}{y}^{\mathrm{3}} \:+\:{z}^{\mathrm{3}} \:=\:\mathrm{195}\:\:\:\:………\:{equation}\:\left({iii}\right) \\ $$$$ \\ $$$${Solve}\:{simultaneously}. \\ $$
Commented by Rasheed Soomro last updated on 11/Sep/16

$${Not}\:{related}\:{to}\:{above} \\ $$$${I}\:{have}\:{corrected}\:{my}\:{answer}\:{to}\:{your}\:{question}\left({Q}#\mathrm{7656}\right) \\ $$$${Pl}\:{see}\:{if}\:{you}\:{have}\:{not}\:{seen}. \\ $$
Commented by Tawakalitu. last updated on 11/Sep/16

$${thanks}\:{have}\:{seen}\:{it},\:{i}\:{really}\:{appreciate}..\:{what}\:{of}\:{this}. \\ $$$${simultaneous} \\ $$
Commented by Rasheed Soomro last updated on 12/Sep/16
![2x + y− z = 8....................(i) x^2 − y^2 + 2z^2 = 14..............(ii) 3x^3 + 4y^3 + z^3 = 195............(iii) (i)⇒z=2x+y−8⇒z^6 =(2x+y−8)^6 ..........................(iv) (ii)⇒z^2 =(1/2)[14−x^2 +y^2 ]⇒z^6 =((1/2)[14−x^2 +y^2 ])^3 ...(v) (iii)⇒z^3 =(195−3x^3 −4y^3 )⇒z^6 =(195−3x^3 −4y^3 )^2 ........(vi) (iv),(v),(vi)⇒ (2x+y−8)^6 =((1/2)[14−x^2 +y^2 ])^3 =(195−3x^3 −4y^3 )^2 (2x+y−8)^6 =((1/2)[14−x^2 +y^2 ])^3 ....................(vii) (2x+y−8)^6 =(195−3x^3 −4y^3 )^2 .........................(viii) (vii)⇒(2x+y−8)^6 −((1/2)[14−x^2 +y^2 ])^3 =0 ⇒[(2x+y−8)^2 ]^3 −((1/2)[14−x^2 +y^2 ])^3 =0 Let (2x+y−8)^2 =A , (1/2)[14−x^2 +y^2 ]=B ⇒A^3 −B^3 =0 ⇒(A−B)(A^2 +AB+B^2 )=0 ⇒A−B=0 ∨ A^2 +AB+B^2 =0 A−B=0⇒(2x+y−8)^2 −(1/2)[14−x^2 +y^2 ]=0 2(2x+y−8)^2 −14+x^2 −y^2 =0 2(4x^2 +y^2 +64+4xy−16y−32x)−14+x^2 −y^2 =0 8x^2 +2y^2 +128+8xy−32y−64x−14+x^2 −y^2 =0 9x^2 +y^2 +114+8xy−32y−64x=0 A^2 +AB+B^2 =0⇒ {(2x+y−8)^2 }^2 +{(2x+y−8)^2 }{(1/2)[14−x^2 +y^2 ]}+{(1/2)[14−x^2 +y^2 ]}^2 =0 (2x+y−8)^4 +{(2x+y−8)^2 }{(1/2)[14−x^2 +y^2 ]}+(1/4)[14−x^2 +y^2 ]^2 =0 (viii)⇒(2x+y−8)^6 −(195−3x^3 −4y^3 )^2 =0 ⇒{(2x+y−8)^3 }^2 −(195−3x^3 −4y^3 )^2 =0 Let (2x+y−8)^3 =a , 195−3x^3 −4y^3 =b ⇒a^2 −b^2 =0 ⇒(a−b)(a+b)=0 ⇒ a−b=0 ∨ a+b=0 a−b=0 ⇒(2x+y−8)^3 −(195−3x^3 −4y^3 )=0 a+b=0 ⇒(2x+y−8)^3 +(195−3x^3 −4y^3 )=0 Continue](https://www.tinkutara.com/question/Q7722.png)
$$\mathrm{2}{x}\:+\:{y}−\:{z}\:=\:\mathrm{8}………………..\left({i}\right) \\ $$$${x}^{\mathrm{2}} \:−\:{y}^{\mathrm{2}} \:+\:\mathrm{2}{z}^{\mathrm{2}} \:=\:\mathrm{14}…………..\left({ii}\right) \\ $$$$\mathrm{3}{x}^{\mathrm{3}} \:+\:\mathrm{4}{y}^{\mathrm{3}} \:+\:{z}^{\mathrm{3}} \:=\:\mathrm{195}…………\left({iii}\right) \\ $$$$\left({i}\right)\Rightarrow{z}=\mathrm{2}{x}+{y}−\mathrm{8}\Rightarrow{z}^{\mathrm{6}} =\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{6}} ……………………..\left({iv}\right) \\ $$$$\left({ii}\right)\Rightarrow{z}^{\mathrm{2}} =\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]\Rightarrow{z}^{\mathrm{6}} =\left(\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]\right)^{\mathrm{3}} …\left({v}\right) \\ $$$$\left({iii}\right)\Rightarrow{z}^{\mathrm{3}} =\left(\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\mathrm{4}{y}^{\mathrm{3}} \right)\Rightarrow{z}^{\mathrm{6}} =\left(\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\mathrm{4}{y}^{\mathrm{3}} \right)^{\mathrm{2}} ……..\left({vi}\right) \\ $$$$ \\ $$$$\left({iv}\right),\left({v}\right),\left({vi}\right)\Rightarrow \\ $$$$\:\:\:\:\:\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{6}} =\left(\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]\right)^{\mathrm{3}} =\left(\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\mathrm{4}{y}^{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$ \\ $$$$\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{6}} =\left(\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]\right)^{\mathrm{3}} ………………..\left({vii}\right) \\ $$$$\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{6}} =\left(\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\mathrm{4}{y}^{\mathrm{3}} \right)^{\mathrm{2}} …………………….\left({viii}\right) \\ $$$$\left({vii}\right)\Rightarrow\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{6}} −\left(\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]\right)^{\mathrm{3}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\left[\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{2}} \right]^{\mathrm{3}} −\left(\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]\right)^{\mathrm{3}} =\mathrm{0} \\ $$$${Let}\:\:\:\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{2}} ={A}\:,\:\:\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]={B} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow{A}^{\mathrm{3}} −{B}^{\mathrm{3}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\left({A}−{B}\right)\left({A}^{\mathrm{2}} +{AB}+{B}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\Rightarrow{A}−{B}=\mathrm{0}\:\:\vee\:\:{A}^{\mathrm{2}} +{AB}+{B}^{\mathrm{2}} =\mathrm{0} \\ $$$${A}−{B}=\mathrm{0}\Rightarrow\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{2}} −\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{2}} −\mathrm{14}+{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{2}\left(\mathrm{4}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{64}+\mathrm{4}{xy}−\mathrm{16}{y}−\mathrm{32}{x}\right)−\mathrm{14}+{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{8}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} +\mathrm{128}+\mathrm{8}{xy}−\mathrm{32}{y}−\mathrm{64}{x}−\mathrm{14}+{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{9}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{114}+\mathrm{8}{xy}−\mathrm{32}{y}−\mathrm{64}{x}=\mathrm{0} \\ $$$${A}^{\mathrm{2}} +{AB}+{B}^{\mathrm{2}} =\mathrm{0}\Rightarrow \\ $$$$\:\left\{\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} +\left\{\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{2}} \right\}\left\{\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]\right\}+\left\{\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]\right\}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{4}} +\left\{\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{2}} \right\}\left\{\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]\right\}+\left(\mathrm{1}/\mathrm{4}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]^{\mathrm{2}} =\mathrm{0} \\ $$$$ \\ $$$$\left({viii}\right)\Rightarrow\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{6}} −\left(\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\mathrm{4}{y}^{\mathrm{3}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\left\{\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{3}} \right\}^{\mathrm{2}} −\left(\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\mathrm{4}{y}^{\mathrm{3}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$${Let}\:\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{3}} ={a}\:,\:\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\mathrm{4}{y}^{\mathrm{3}} ={b} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\left({a}−{b}\right)\left({a}+{b}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:{a}−{b}=\mathrm{0}\:\:\vee\:{a}+{b}=\mathrm{0} \\ $$$${a}−{b}=\mathrm{0}\:\Rightarrow\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{3}} −\left(\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\mathrm{4}{y}^{\mathrm{3}} \right)=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$${a}+{b}=\mathrm{0}\:\Rightarrow\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{3}} +\left(\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\mathrm{4}{y}^{\mathrm{3}} \right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$$${Continue} \\ $$
Commented by Tawakalitu. last updated on 12/Sep/16
$${Thannks}\:{so}\:{much}\:{sir}.\:{am}\:{with}\:{you}\:{sir}. \\ $$
Commented by Rasheed Soomro last updated on 14/Sep/16
![2x + y− z = 8....................(i) x^2 − y^2 + 2z^2 = 14..............(ii) 3x^3 + 4y^3 + z^3 = 195...........(iii) (i)⇒ z=2x+y−8...................(iv) (ii)⇒z^2 =(1/2)[14−x^2 +y^2 ].......(v) (iii)⇒z^3 =195−3x^3 − 4y^3 ...........(vi) (ii)÷(i)⇒ z=(((1/2)[14−x^2 +y^2 ])/(2x+y−8))........(vii) (iii)÷(ii)⇒z=((195−3x^3 − 4y^3 )/((1/2)[14−x^2 +y^2 ]))........(viii) (vii),(viii)⇒(((1/2)[14−x^2 +y^2 ])/(2x+y−8))=((195−3x^3 − 4y^3 )/((1/2)[14−x^2 +y^2 ])) {(1/2)[14−x^2 +y^2 ]}^2 =(2x+y−8)(195−3x^3 − 4y^3 ) [14−x^2 +y^2 ]^2 =4(2x+y−8)(195−3x^3 − 4y^3 )............A (vi)÷(iv)⇒z^2 =((195−3x^3 − 4y^3 )/(2x+y−8))..............(ix) (v)⇒ z^2 =(1/2)[14−x^2 +y^2 ]..........(x) (ix),(x)⇒ ((195−3x^3 − 4y^3 )/(2x+y−8))=(1/2)[14−x^2 +y^2 ] 2(195−3x^3 − 4y^3 )=(2x+y−8)(14−x^2 +y^2 ).....B (i)^2 ⇒z^2 =(2x+y−8)^2 ........................(xi) (ii)⇒z^2 =(1/2)[14−x^2 +y^2 ].................(xii) (xi),(xii)⇒(2x+y−8)^2 =(1/2)[14−x^2 +y^2 ] ⇒2(2x+y−8)^2 =14−x^2 +y^2 ⇒2(4x^2 +y^2 +64+4xy−16y−32x)=14−x^2 +y^2 ⇒8x^2 +2y^2 +128+8xy−32y−64x−14+x^2 −y^2 =0 ⇒9x^2 +y^2 +8xy−32y−64x+114...........................C (iv)^3 ⇒z^3 =(2x+y−8)^3 ....................(xiii) (vi)⇒ z^3 =195−3x^3 − 4y^3 ................(xiv) (xiii),(xiv)⇒(2x+y−8)^3 =195−3x^3 − 4y^3 .....................D Continue](https://www.tinkutara.com/question/Q7742.png)
$$\mathrm{2}{x}\:+\:{y}−\:{z}\:=\:\mathrm{8}………………..\left({i}\right) \\ $$$${x}^{\mathrm{2}} \:−\:{y}^{\mathrm{2}} \:+\:\mathrm{2}{z}^{\mathrm{2}} \:=\:\mathrm{14}…………..\left({ii}\right) \\ $$$$\mathrm{3}{x}^{\mathrm{3}} \:+\:\mathrm{4}{y}^{\mathrm{3}} \:+\:{z}^{\mathrm{3}} \:=\:\mathrm{195}………..\left({iii}\right) \\ $$$$ \\ $$$$\left({i}\right)\Rightarrow\:\:{z}=\mathrm{2}{x}+{y}−\mathrm{8}……………….\left({iv}\right) \\ $$$$\left({ii}\right)\Rightarrow{z}^{\mathrm{2}} =\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]…….\left({v}\right) \\ $$$$\left({iii}\right)\Rightarrow{z}^{\mathrm{3}} =\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\:\mathrm{4}{y}^{\mathrm{3}} ………..\left({vi}\right) \\ $$$$ \\ $$$$\left({ii}\right)\boldsymbol{\div}\left({i}\right)\Rightarrow\:\:{z}=\frac{\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]}{\mathrm{2}{x}+{y}−\mathrm{8}}……..\left({vii}\right) \\ $$$$\left({iii}\right)\boldsymbol{\div}\left({ii}\right)\Rightarrow{z}=\frac{\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\:\mathrm{4}{y}^{\mathrm{3}} }{\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]}……..\left({viii}\right) \\ $$$$\left({vii}\right),\left({viii}\right)\Rightarrow\frac{\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]}{\mathrm{2}{x}+{y}−\mathrm{8}}=\frac{\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\:\mathrm{4}{y}^{\mathrm{3}} }{\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]} \\ $$$$\left\{\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]\right\}^{\mathrm{2}} =\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)\left(\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\:\mathrm{4}{y}^{\mathrm{3}} \right) \\ $$$$\:\:\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]^{\mathrm{2}} =\mathrm{4}\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)\left(\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\:\mathrm{4}{y}^{\mathrm{3}} \right)…………{A} \\ $$$$ \\ $$$$\left({vi}\right)\boldsymbol{\div}\left({iv}\right)\Rightarrow{z}^{\mathrm{2}} =\frac{\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\:\mathrm{4}{y}^{\mathrm{3}} }{\mathrm{2}{x}+{y}−\mathrm{8}}…………..\left({ix}\right) \\ $$$$\left({v}\right)\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:{z}^{\mathrm{2}} =\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]……….\left({x}\right) \\ $$$$\left({ix}\right),\left({x}\right)\Rightarrow\:\frac{\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\:\mathrm{4}{y}^{\mathrm{3}} }{\mathrm{2}{x}+{y}−\mathrm{8}}=\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\left(\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\:\mathrm{4}{y}^{\mathrm{3}} \right)=\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)\left(\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)…..{B} \\ $$$$\left({i}\right)^{\mathrm{2}} \Rightarrow{z}^{\mathrm{2}} =\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{2}} ……………………\left({xi}\right) \\ $$$$\left({ii}\right)\Rightarrow{z}^{\mathrm{2}} =\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right]……………..\left({xii}\right) \\ $$$$\left({xi}\right),\left({xii}\right)\Rightarrow\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{2}} =\left(\mathrm{1}/\mathrm{2}\right)\left[\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{2}\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{2}} =\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{2}\left(\mathrm{4}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{64}+\mathrm{4}{xy}−\mathrm{16}{y}−\mathrm{32}{x}\right)=\mathrm{14}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{8}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} +\mathrm{128}+\mathrm{8}{xy}−\mathrm{32}{y}−\mathrm{64}{x}−\mathrm{14}+{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{9}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{8}{xy}−\mathrm{32}{y}−\mathrm{64}{x}+\mathrm{114}………………………{C} \\ $$$$ \\ $$$$\left({iv}\right)^{\mathrm{3}} \Rightarrow{z}^{\mathrm{3}} =\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{3}} ………………..\left({xiii}\right) \\ $$$$\left({vi}\right)\Rightarrow\:\:{z}^{\mathrm{3}} =\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\:\mathrm{4}{y}^{\mathrm{3}} …………….\left({xiv}\right) \\ $$$$\left({xiii}\right),\left({xiv}\right)\Rightarrow\left(\mathrm{2}{x}+{y}−\mathrm{8}\right)^{\mathrm{3}} =\mathrm{195}−\mathrm{3}{x}^{\mathrm{3}} −\:\mathrm{4}{y}^{\mathrm{3}} …………………{D} \\ $$$$ \\ $$$$ \\ $$$$\:{Continue}\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by Tawakalitu. last updated on 13/Sep/16
$${Am}\:{with}\:{you}\:{sir}.\:{thanks}\:{for}\:{your}\:{help}. \\ $$
