Question Number 10241 by FilupSmith last updated on 31/Jan/17
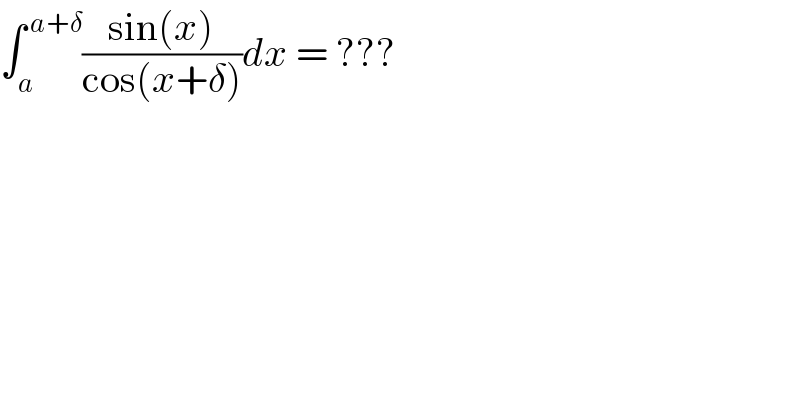
$$\int_{{a}} ^{\:{a}+\delta} \frac{\mathrm{sin}\left({x}\right)}{\mathrm{cos}\left({x}+\delta\right)}{dx}\:=\:??? \\ $$
Commented by prakash jain last updated on 31/Jan/17
![((sin(x))/(cos(x+δ)))=((sin(x+δ−δ))/(cos(x+δ))) =((sin (x+δ)cos δ−cos (x+δ)sin δ)/(cos (x+δ))) =tan (x+δ)cos δ−sin δ ∫_a ^(a+δ) (tan (x+δ)cos δ−sin δ)dx =[−cos δln cos (x+δ)−xsin δ]_a ^(a+δ) =[−cos δln ((cos (a+δ))/(cos a))−δsin δ]](https://www.tinkutara.com/question/Q10249.png)
$$\frac{\mathrm{sin}\left({x}\right)}{\mathrm{cos}\left({x}+\delta\right)}=\frac{\mathrm{sin}\left({x}+\delta−\delta\right)}{\mathrm{cos}\left({x}+\delta\right)} \\ $$$$=\frac{\mathrm{sin}\:\left({x}+\delta\right)\mathrm{cos}\:\delta−\mathrm{cos}\:\left({x}+\delta\right)\mathrm{sin}\:\delta}{\mathrm{cos}\:\left({x}+\delta\right)} \\ $$$$=\mathrm{tan}\:\left({x}+\delta\right)\mathrm{cos}\:\delta−\mathrm{sin}\:\delta \\ $$$$\int_{{a}} ^{{a}+\delta} \left(\mathrm{tan}\:\left({x}+\delta\right)\mathrm{cos}\:\delta−\mathrm{sin}\:\delta\right){dx} \\ $$$$=\left[−\mathrm{cos}\:\delta\mathrm{ln}\:\mathrm{cos}\:\left({x}+\delta\right)−{x}\mathrm{sin}\:\delta\right]_{{a}} ^{{a}+\delta} \\ $$$$=\left[−\mathrm{cos}\:\delta\mathrm{ln}\:\frac{\mathrm{cos}\:\left({a}+\delta\right)}{\mathrm{cos}\:{a}}−\delta\mathrm{sin}\:\delta\right] \\ $$
