Question Number 1603 by 123456 last updated on 25/Aug/15
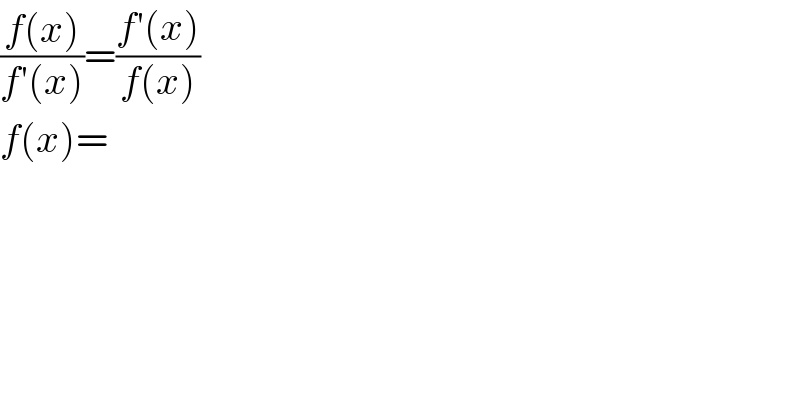
$$\frac{{f}\left({x}\right)}{{f}'\left({x}\right)}=\frac{{f}'\left({x}\right)}{{f}\left({x}\right)} \\ $$$${f}\left({x}\right)= \\ $$
Answered by Rasheed Soomro last updated on 28/Aug/15
![[ f ′(x) ]^2 =[ f(x) ]^2 f ′(x)=±f(x) Let f(x)=y (dy/dx)=±y⇒((1/y)) (dy/dx)=±1 ⇒∫[((1/y)) (dy/dx)]dx=∫(±1)dx ln∣y∣+c=±x+c ln∣y∣=±x+c y=e^(±x+c) =e^(±x) .e^c =ke^(±x) f(x)=ke^(±x)](https://www.tinkutara.com/question/Q1604.png)
$$\left[\:{f}\:'\left({x}\right)\:\right]^{\mathrm{2}} =\left[\:{f}\left({x}\right)\:\right]^{\mathrm{2}} \\ $$$${f}\:'\left({x}\right)=\pm{f}\left({x}\right) \\ $$$${Let}\:{f}\left({x}\right)={y}\: \\ $$$$\frac{{dy}}{{dx}}=\pm{y}\Rightarrow\left(\frac{\mathrm{1}}{{y}}\right)\:\frac{{dy}}{{dx}}=\pm\mathrm{1}\: \\ $$$$\Rightarrow\int\left[\left(\frac{\mathrm{1}}{{y}}\right)\:\frac{{dy}}{{dx}}\right]{dx}=\int\left(\pm\mathrm{1}\right){dx} \\ $$$${ln}\mid{y}\mid+{c}=\pm{x}+{c} \\ $$$${ln}\mid{y}\mid=\pm{x}+{c} \\ $$$${y}={e}^{\pm{x}+{c}} ={e}^{\pm{x}} .{e}^{{c}} ={ke}^{\pm{x}} \\ $$$${f}\left({x}\right)={ke}^{\pm{x}} \\ $$
Commented by 123456 last updated on 27/Aug/15
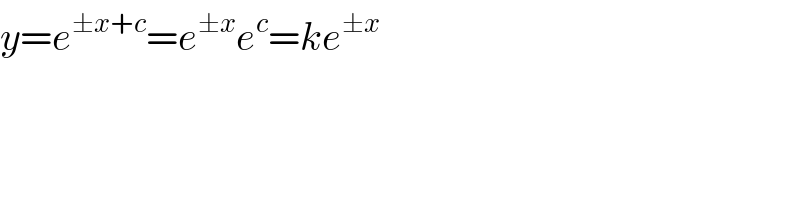
$${y}={e}^{\pm{x}+{c}} ={e}^{\pm{x}} {e}^{{c}} ={ke}^{\pm{x}} \\ $$
Commented by Rasheed Soomro last updated on 27/Aug/15

$$\boldsymbol{\mathrm{Thanks}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{mentioning}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{correcting}}\:\boldsymbol{\mathrm{my}}\:\boldsymbol{\mathrm{mistake}}. \\ $$$$\boldsymbol{\mathrm{Pl}}\:\boldsymbol{\mathrm{continue}}\:\boldsymbol{\mathrm{same}}\:\boldsymbol{\mathrm{practice}}\:\boldsymbol{\mathrm{as}}\:\boldsymbol{\mathrm{I}}\:\boldsymbol{\mathrm{want}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{learn}}. \\ $$
